推論-三段論法
ギリシャ人によって与えられた三段論法の意味は Deduction。それは一種の論理的な議論です。
いくつかの重要な用語の定義
三段論法の問題を解決する上で重要な役割を果たすいくつかの用語を以下に示します。
Proposition−命題は声明を出す文です。命題は、a)主語、b)述語、c)主語と述語の関係の3つの部分で構成されます。いくつかの提案を以下に示します。
- すべての海岸はビーチです。
- 正直な生徒はいません。
- 一部の文書は秘密です。
Subject and Predicate−主題は、何かが言われている部分です。一方、述語は主語に関連する部分です。たとえば、上記の命題から、海岸、学生、文書は主題であり、ビーチ、正直、秘密は述語です。
分類命題の種類
Universal Proposition−普遍的な命題は、主題を完全に含むか、完全に除外するかのいずれかです。たとえば-頭のいい生徒はいません。普遍的な命題はさらに次のように分類されます-
Universal positive proposition −フォームが all X are Yそれからそれは前向きな命題と呼ばれます。それは一般的に文字で示されますA。
Universal negative proposition −フォームが no X are T、それからそれは否定的な命題と呼ばれます。それはによって示されますE。
Particular proposition−主題を部分的に示すか、部分的にではなく完全に除外するという命題です。たとえば、一部の猫は綿です。また、以下のタイプに分けられます-
Particular positive proposition −次のような形式 some X are U特定の前向きな命題と呼ばれます。それらは次のようにコード化されますI。
Particular negative proposition −次のような形式 Some T are not P 例えば、 some cats are not coils 特定の否定命題と呼ばれ、次のようにコード化されます O。
Mediate inference−ここで、結論は2つのステートメントから得られます。例-「すべての唇はコイルです」および「すべてのボールはコウモリです」。したがって、結論は「すべての唇はコイルです」ということになります。
Immediate inference−ここで、結論は1つの命題からのみ得られます。たとえば、ステートメントが「すべての教師は神である」である場合、結論は「一部の教師は神である」になります。
即時推論の2つの重要な方法
これらの方法には、変換、対偶などが含まれます。
Implications−「すべての猫が浜辺である」とすると、「一部の猫は浜辺である」という結論が正しいことを示しています。したがって、与えられた命題がAカテゴリのものである場合、それはIタイプの結論が真でなければならないことも示しています。
Conversion −2つのステップで構成されています。
Step 1 −サブジェクトは述語に変換され、その逆も同様です。
Step 2 −与えられた命題はそれに応じて変更されます。
For Example −
Statements−すべての猫はラックです。バッグはすべてラックです。いくつかの財布はバッグです。
Conclusions −
1.一部の猫はバッグです。
2.一部のラックは猫です。
3.一部のラックは財布です。
A - 1のみ
B -2と3のみ
C -1と2のみ
D -1と3のみ
Solution −
回答-オプションB
命題を表現する絵画的な方法は、オイラーによって策定されています。4つの命題に従って関係を作ることができる4つの方法があります。
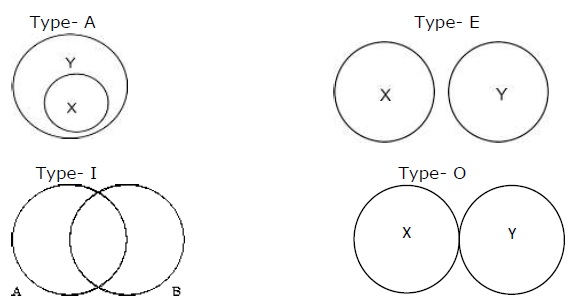
Type-Aは「AllXare Y」、Type-Eは「NoX are Y」、Type-Iは「SomeA are B」、Type-Oは「SomeX arenotY」を表します。
For Example −
Statements −一部のカメラはラップトップです。
一部のラップトップは電話です。
一部の電話はタブレットです。
Conclusions −
I-少なくとも一部のタブレットはカメラです
II-すべてのタブレットがラップトップである可能性があります
III-どのタブレットもラップトップではありません
Solution −
円線図−
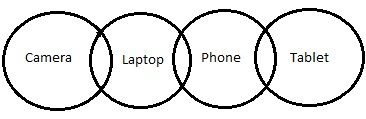
上の図のように、
結論IIIは次のとおりです。しかし、「可能性」という言葉は声明の中で言及されています。それでは、可能性を確認しましょう。
新しい図は次のようになります-
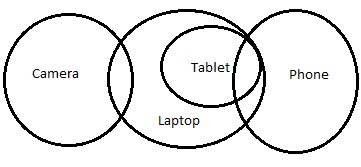
しかし、この場合、結論IIIは続きません。結論IIまたは結論IIIのいずれかが続きます。