Analiza finansowa danych programu Excel
Możesz w łatwy sposób przeprowadzić analizę finansową za pomocą programu Excel. Excel zapewnia kilka funkcji finansowych, takich jak PMT, PV, NPV, XNPV, IRR, MIRR, XIRR i tak dalej, które umożliwiają szybkie uzyskanie wyników analizy finansowej.
W tym rozdziale dowiesz się, gdzie i jak możesz używać tych funkcji do analizy.
Co to jest renta?
Renta to seria stałych płatności gotówkowych dokonywanych w ciągłym okresie. Na przykład oszczędności na emeryturę, płatności ubezpieczeniowe, kredyt mieszkaniowy, hipoteka itp. W funkcjach rentowych -
- Liczba dodatnia oznacza otrzymaną gotówkę.
- Liczba ujemna oznacza wypłaconą gotówkę.
Wartość bieżąca serii przyszłych płatności
Wartość bieżąca to całkowita kwota, jaką jest teraz warta seria przyszłych płatności. Możesz obliczyć wartość bieżącą za pomocą funkcji programu Excel -
PV- Oblicza bieżącą wartość inwestycji przy użyciu stopy procentowej i serii przyszłych płatności (wartości ujemne) i dochodu (wartości dodatnie). Co najmniej jeden z przepływów pieniężnych musi być dodatni, a co najmniej jeden ujemny.
NPV - Oblicza bieżącą wartość netto inwestycji przy użyciu stopy dyskontowej i serii okresowych przyszłych płatności (wartości ujemne) i dochodu (wartości dodatnie).
XNPV - Oblicza wartość bieżącą netto dla harmonogramu przepływów pieniężnych, który niekoniecznie jest okresowy.
Note that -
Przepływy pieniężne PV muszą być stałe, podczas gdy przepływy pieniężne NPV mogą być zmienne.
Przepływy pieniężne PV mogą występować na początku lub na końcu okresu, podczas gdy przepływy pieniężne NPV muszą występować na końcu okresu.
Przepływy pieniężne NPV muszą być okresowe, podczas gdy przepływy pieniężne XNPV nie muszą być okresowe.
W tej sekcji dowiesz się, jak pracować z PV. Dowiesz się o NPV w dalszej części.
Przykład
Załóżmy, że kupujesz lodówkę. Sprzedawca podaje, że cena lodówki to 32000, ale masz możliwość spłaty kwoty w ciągu 8 lat z oprocentowaniem 13% w skali roku i rocznymi płatnościami 6000. Masz również możliwość dokonywania płatności. na początku lub na końcu każdego roku.
Chcesz wiedzieć, która z tych opcji jest dla Ciebie korzystna.
Możesz użyć funkcji Excel PV -
PV (rate, nper, pmt, [fv ], [type])Aby obliczyć wartość bieżącą z płatnościami na koniec każdego roku, pomiń typ lub podaj 0 jako typ.
Aby obliczyć wartość bieżącą z płatnościami na koniec każdego roku, podaj 1 jako typ.

Otrzymasz następujące wyniki -

W związku z tym,
- Jeśli dokonasz płatności teraz, musisz zapłacić 32 000 bieżącej wartości.
- Jeśli zdecydujesz się na płatności roczne z płatnością na koniec roku, musisz zapłacić 28 793 bieżącej wartości.
- Jeśli zdecydujesz się na płatności roczne z płatnością na koniec roku, musisz zapłacić 32 536 bieżącej wartości.
Możesz wyraźnie zobaczyć, że opcja 2 jest dla Ciebie korzystna.
Co to jest EMI?
Rata równa miesięczna (EMI) jest definiowana przez Investopedię jako „Stała kwota płatności dokonywana przez pożyczkobiorcę na rzecz pożyczkodawcy w określonym dniu każdego miesiąca kalendarzowego. Zrównane raty miesięczne służą do spłaty zarówno odsetek, jak i kwoty głównej każdego miesiąca, tak aby ponad przez określoną liczbę lat, pożyczka zostanie spłacona w całości. "
EMI na pożyczce
W Excelu możesz obliczyć EMI dla pożyczki za pomocą funkcji PMT.
Załóżmy, że chcesz wziąć pożyczkę domową w wysokości 5000000 z roczną stopą procentową 11,5% i okresem spłaty pożyczki 25 lat. Możesz znaleźć swój EMI w następujący sposób -
- Oblicz stopę procentową na miesiąc (stopa procentowa w skali roku / 12)
- Oblicz liczbę miesięcznych płatności (liczba lat * 12)
- Użyj funkcji PMT do obliczenia EMI

Jak obserwujesz,
- Wartość bieżąca (PV) to kwota pożyczki.
- Wartość przyszła (FV) wynosi 0, ponieważ na koniec okresu kwota pożyczki powinna wynosić 0.
- Typ to 1, ponieważ EMI są opłacane na początku każdego miesiąca.
Otrzymasz następujące wyniki -

Miesięczna spłata kwoty głównej i odsetek od pożyczki
EMI obejmuje zarówno odsetki, jak i część spłaty kapitału. Wraz z upływem czasu te dwa składniki EMI będą się zmieniać, zmniejszając równowagę.
Aby dostać
Część odsetkową swoich miesięcznych płatności możesz skorzystać z funkcji Excel IPMT.
Spłatę głównej części swoich miesięcznych płatności możesz skorzystać z funkcji Excel PPMT.
Na przykład, jeśli zaciągnąłeś pożyczkę w wysokości 1 000 000 na okres 8 miesięcy w wysokości 16% w skali roku. Możesz uzyskać wartości dla EIW, malejące kwoty odsetek, rosnącą spłatę kwot kapitału i malejące saldo pożyczki w ciągu 8 miesięcy. Na koniec 8 miesięcy saldo pożyczki wyniesie 0.
Postępuj zgodnie z procedurą podaną poniżej.
Step 1 - Obliczyć EMI w następujący sposób.

Powoduje to EMI Rs. 13261,59.

Step 2 - Następnie oblicz odsetki i główne części EIW na 8 miesięcy, jak pokazano poniżej.

Otrzymasz następujące wyniki.

Odsetki i kwota główna płatne między dwoma okresami
Możesz obliczyć odsetki i kwotę główną zapłacone między dwoma okresami włącznie.
Obliczyć łączny odsetek płatnego między 2 ND i 3 rd miesiące z wykorzystaniem funkcji CUMIPMT.
Zweryfikować wynik sumując wartości procentowe dla 2 ND i 3 rd miesięcy.
Obliczyć skumulowaną kapitału płatnego między 2 nd i 3 rd miesięcy wykorzystaniem funkcji CUMPRINC.
Zweryfikować wynik podsumowujący główne wartości 2 ND i 3 rd miesięcy.

Otrzymasz następujące wyniki.

Możesz zobaczyć, że Twoje obliczenia są zgodne z wynikami weryfikacji.
Obliczanie stopy procentowej
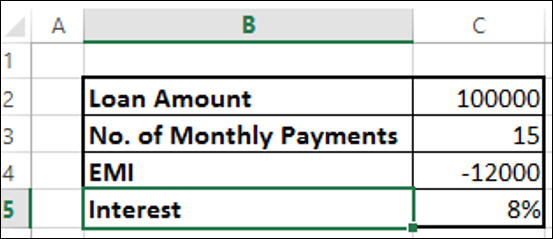
Załóżmy, że bierzesz pożyczkę w wysokości 100 000 i chcesz spłacić ją w ciągu 15 miesięcy z maksymalną miesięczną spłatą w wysokości 12 000. Możesz chcieć poznać stopę procentową, według której musisz spłacać.
Znajdź stopę procentową za pomocą funkcji Excel RATE -

Otrzymasz wynik jako 8%.
Obliczanie terminu pożyczki
Załóżmy, że bierzesz pożyczkę w wysokości 100 000 z oprocentowaniem 10%. Chcesz maksymalnej miesięcznej płatności w wysokości 15 000. Możesz chcieć wiedzieć, ile czasu zajmie spłata pożyczki.
Znajdź liczbę płatności za pomocą funkcji Excel NPER

Wynik otrzymasz jako 12 miesięcy.

Decyzje dotyczące inwestycji
Kiedy chcesz dokonać inwestycji, porównujesz różne opcje i wybierasz tę, która daje lepsze zwroty. Wartość bieżąca netto jest przydatna przy porównywaniu przepływów pieniężnych w okresie i decydowaniu, który z nich jest lepszy. Przepływy pieniężne mogą występować w regularnych, okresowych odstępach czasu lub w nieregularnych odstępach czasu.
Najpierw rozważymy przypadek regular, periodical cash flows.
Wartość bieżąca netto sekwencji przepływów pieniężnych otrzymanych w różnych punktach w czasie za n lat od teraz (n może być ułamkiem) wynosi 1/(1 + r)n, gdzie r jest roczną stopą procentową.
Rozważ następujące dwie inwestycje w okresie 3 lat.
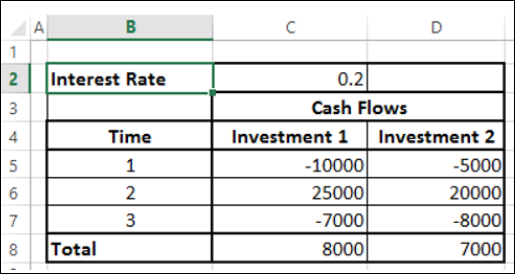
Przy wartości nominalnej Inwestycja 1 wygląda lepiej niż Inwestycja 2. Możesz jednak zdecydować, która inwestycja jest lepsza tylko wtedy, gdy znasz prawdziwą wartość inwestycji na dzień dzisiejszy. Możesz użyć funkcji NPV do obliczenia zwrotów.
Mogą wystąpić przepływy pieniężne
- Pod koniec każdego roku.
- Na początku każdego roku.
- W połowie każdego roku.
Funkcja NPV zakłada, że przepływy pieniężne są na koniec roku. Jeśli przepływy pieniężne występują w różnym czasie, należy wziąć pod uwagę ten konkretny czynnik wraz z obliczeniem wartości NPV.
Załóżmy, że przepływy pieniężne wystąpią pod koniec roku. Następnie możesz od razu skorzystać z funkcji NPV.
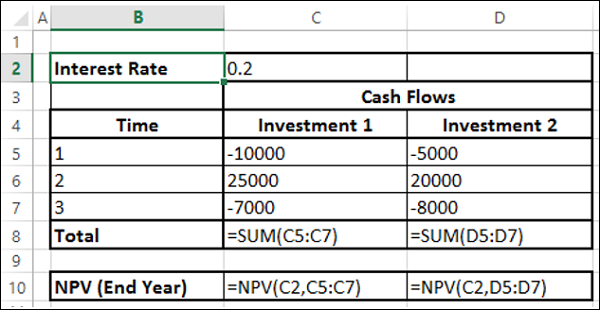
Otrzymasz następujące wyniki -

Jak widać, NPV dla Inwestycji 2 jest wyższe niż dla Inwestycji 1. Dlatego też Inwestycja 2 jest lepszym wyborem. Otrzymałeś ten wynik, ponieważ wypływy pieniężne z Inwestycji 2 są w późniejszych okresach w porównaniu z przepływami z Inwestycji 1.
Przepływy pieniężne na początku roku
Załóżmy, że przepływy pieniężne występują na początku każdego roku. W takim przypadku nie należy uwzględniać pierwszego przepływu pieniężnego w obliczeniach NPV, ponieważ przedstawia on już wartość bieżącą. Musisz dodać pierwszy przepływ pieniężny do wartości bieżącej netto uzyskanej z pozostałych przepływów pieniężnych, aby uzyskać wartość bieżącą netto.

Otrzymasz następujące wyniki -

Przepływy pieniężne w połowie roku
Załóżmy, że przepływy pieniężne występują w połowie każdego roku. W takim przypadku musisz pomnożyć wartość bieżącą netto uzyskaną z przepływów pieniężnych przez $ \ sqrt {1 + r} $, aby uzyskać bieżącą wartość netto.

Otrzymasz następujące wyniki -

Przepływy pieniężne w nieregularnych odstępach czasu
Jeśli chcesz obliczyć wartość bieżącą netto z nieregularnymi przepływami pieniężnymi, tj. Przepływami pieniężnymi występującymi w przypadkowych momentach, obliczenia są nieco skomplikowane.
Jednak w Excelu możesz łatwo wykonać takie obliczenia za pomocą funkcji XNPV.
- Uporządkuj swoje dane według dat i przepływów pieniężnych.
Note- Pierwsza data w danych powinna być najwcześniejsza ze wszystkich dat. Pozostałe daty mogą występować w dowolnej kolejności.
- Użyj funkcji XNPV, aby obliczyć wartość bieżącą netto.
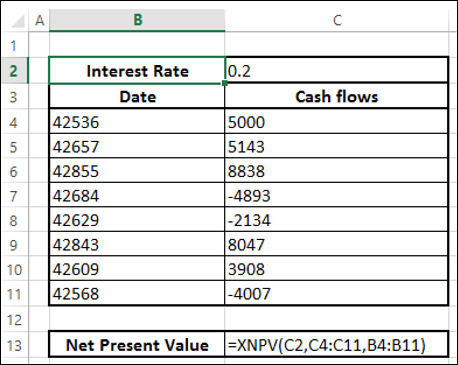
Otrzymasz następujące wyniki -

Załóżmy, że dzisiejsza data jest 15 th marca 2015. Jak można zauważyć, wszystkie daty przepływów pieniężnych są późniejszych terminach. Jeśli chcesz znaleźć bieżącą wartość netto na dzień dzisiejszy, uwzględnij ją w danych u góry i określ 0 dla przepływu środków pieniężnych.

Otrzymasz następujące wyniki -

Wewnętrzna stopa zwrotu (IRR)
Wewnętrzna stopa zwrotu (IRR) z inwestycji to stopa procentowa, przy której wartość bieżąca netto wynosi 0. Jest to wartość stopy, dla której bieżące wartości dodatnich przepływów pieniężnych dokładnie kompensują wartości ujemne. Gdy stopą dyskontową jest IRR, inwestycja jest całkowicie obojętna, tzn. Inwestor nie zyskuje ani nie traci pieniędzy.
Weź pod uwagę następujące przepływy pieniężne, różne stopy procentowe i odpowiadające im wartości NPV.

Jak widać pomiędzy wartościami stopy procentowej 10% i 11%, zmienia się znak NPV. Kiedy precyzyjnie dostosujesz stopę procentową do 10,53%, wartość bieżąca netto wynosi prawie 0. W związku z tym IRR wynosi 10,53%.
Określanie IRR przepływów pieniężnych dla projektu
Możesz obliczyć IRR przepływów pieniężnych za pomocą funkcji IRR programu Excel.

IRR wynosi 10,53%, jak widzieliście w poprzedniej sekcji.
Dla danych przepływów pieniężnych IRR może -
- istnieją i są niepowtarzalne
- istnieje i wiele
- nie istnieje
Unikalny IRR
Jeśli IRR istnieje i jest wyjątkowy, można go wykorzystać do wybrania najlepszej inwestycji spośród kilku możliwości.
Jeśli pierwszy przepływ gotówki jest ujemny, oznacza to, że inwestor ma pieniądze i chce zainwestować. Wtedy im wyższa IRR, tym lepiej, ponieważ reprezentuje stopę procentową otrzymywaną przez inwestora.
Jeśli pierwszy przepływ środków pieniężnych jest dodatni, oznacza to, że inwestor potrzebuje pieniędzy i szuka pożyczki, im niższa IRR, tym lepiej, ponieważ odzwierciedla stopę procentową, którą płaci inwestor.
Aby sprawdzić, czy IRR jest niepowtarzalny, czy nie, zmień domyślną wartość i oblicz IRR. Jeśli IRR pozostaje stała, jest wyjątkowa.

Jak zauważyłeś, IRR ma unikalną wartość dla różnych wartości domyślnych.

Wiele IRR
W niektórych przypadkach możesz mieć wiele IRR. Rozważ następujące przepływy pieniężne. Oblicz IRR z różnymi wartościami domyślnymi.

Otrzymasz następujące wyniki -

Można zauważyć, że istnieją dwie IRR - -9,59% i 216,09%. Możesz zweryfikować te dwa IRR obliczające NPV.

Zarówno dla -9,59%, jak i 216,09% NPV wynosi 0.
Brak IRR
W niektórych przypadkach możesz nie mieć IRR. Rozważ następujące przepływy pieniężne. Oblicz IRR z różnymi wartościami domyślnymi.

Otrzymasz wynik jako #NUM dla wszystkich domyślnych wartości.

Wynik #NUM oznacza, że nie ma IRR dla rozważanych przepływów pieniężnych.
Schematy przepływów pieniężnych i wewnętrzna stopa zwrotu
Jeśli w przepływach pieniężnych występuje tylko jedna zmiana znaku, na przykład z ujemnego na dodatni lub z dodatniego na ujemny, gwarantowana jest unikalna wewnętrzna stopa zwrotu. Na przykład w przypadku inwestycji kapitałowych pierwszy przepływ środków pieniężnych będzie ujemny, a pozostałe przepływy będą dodatnie. W takich przypadkach istnieje niepowtarzalna wewnętrzna stopa zwrotu.
Jeśli w przepływach pieniężnych następuje więcej niż jedna zmiana znaku, IRR może nie istnieć. Nawet jeśli istnieje, może nie być wyjątkowy.
Decyzje oparte na IRR
Wielu analityków woli używać IRR i jest to popularna miara rentowności, ponieważ wyrażona procentowo jest łatwa do zrozumienia i łatwa do porównania z wymaganym zwrotem. Jednak podczas podejmowania decyzji z IRR pojawiają się pewne problemy. Jeśli masz rangę z IRR i podejmujesz decyzje na podstawie tych rang, możesz skończyć z błędnymi decyzjami.
Widzieliście już, że NPV umożliwi podejmowanie decyzji finansowych. Jednak IRR i NPV nie zawsze prowadzą do tej samej decyzji, gdy projekty wzajemnie się wykluczają.
Mutually exclusive projectsto takie, w przypadku których wybór jednego projektu wyklucza akceptację innego. Gdy porównywane projekty wykluczają się wzajemnie, może powstać konflikt rankingowy między wartością bieżącą netto a wewnętrzną stopą zwrotu. Jeśli musisz wybrać między projektem A i projektem B, NPV może sugerować akceptację projektu A, podczas gdy IRR może sugerować projekt B.
Ten rodzaj konfliktu między NPV a IRR może wynikać z jednej z następujących przyczyn -
- Projekty mają bardzo różne rozmiary, lub
- Czas przepływów pieniężnych jest inny.
Projekty o znacznej różnicy wielkości
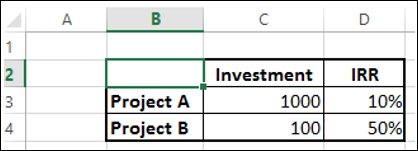
Jeśli chcesz podjąć decyzję przez IRR, projekt A daje zwrot w wysokości 100, a projekt B zwrot w wysokości 50. W związku z tym inwestycja w projekt A wygląda na opłacalną. To jednak zła decyzja ze względu na różnicę w skali projektów.
Rozważ -
Masz 1000 do zainwestowania.
Jeśli zainwestujesz całe 1000 w projekt A, otrzymasz zwrot w wysokości 100.
Jeśli zainwestujesz 100 w projekt B, nadal będziesz mieć w ręku 900, które możesz zainwestować w inny projekt, powiedzmy projekt C. Załóżmy, że uzyskasz zwrot w wysokości 20% z projektu C, a następnie całkowity zwrot z projektu B i projektu C wynosi 230, co znacznie wyprzedza rentowność.
Dlatego NPV jest lepszym sposobem podejmowania decyzji w takich przypadkach.
Projekty z różnymi terminami przepływów pieniężnych

Ponownie, jeśli weźmiesz pod uwagę IRR, aby zdecydować, projekt B byłby wyborem. Jednak projekt A ma wyższą wartość NPV i jest idealnym wyborem.
Wewnętrzna stopa zwrotu z nieregularnie rozłożonych przepływów pieniężnych (XIRR)
Twoje przepływy pieniężne mogą czasami być nieregularne. W takim przypadku nie można użyć IRR, ponieważ IRR wymaga równo rozłożonych odstępów czasu. Zamiast tego możesz użyć XIRR, który uwzględnia daty przepływów pieniężnych wraz z przepływami pieniężnymi.

Wynikająca z tego wewnętrzna stopa zwrotu wynosi 26,42%.

Zmodyfikowana IRR (MIRR)
Rozważ przypadek, w którym Twoja stopa finansowa różni się od stopy reinwestycji. Jeśli obliczysz wewnętrzną stopę zwrotu za pomocą IRR, przyjmuje ona tę samą stopę zarówno dla finansów, jak i dla reinwestycji. Co więcej, możesz również uzyskać wiele IRR.
Na przykład rozważ przepływy pieniężne podane poniżej -

Jak widać, wartość NPV wynosi 0 więcej niż raz, co powoduje wiele IRR. Ponadto nie jest brana pod uwagę stopa reinwestycji. W takich przypadkach możesz użyć zmodyfikowanej IRR (MIRR).

Otrzymasz wynik 7%, jak pokazano poniżej -

Note - W przeciwieństwie do IRR, MIRR zawsze będzie wyjątkowy.