Exemplo de problema de circuitos equivalentes

No capítulo anterior, discutimos sobre os circuitos equivalentes de combinação em série e combinação paralela individualmente. Neste capítulo, vamos resolver um problema de exemplo considerando as combinações em série e paralelas de elementos passivos semelhantes.

Exemplo

Deixe-nos encontrar o equivalent resistance através dos terminais A e B da seguinte rede elétrica.

Obteremos a resistência equivalente nos terminais A e B minimizando a rede acima em um único resistor entre esses dois terminais. Para isso, temos queidentify the combination of resistors que são conectados em forma de série e forma paralela e, em seguida, encontram a resistência equivalente da respectiva forma em cada etapa.

A rede elétrica fornecida é modified no seguinte formato, conforme mostrado na figura a seguir.

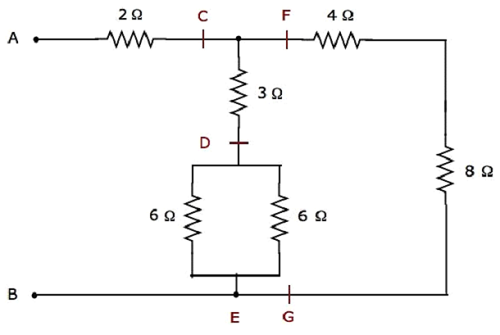
Na figura acima, as letras, C a G, são usadas para rotular vários terminais.

Step 1 - Na rede acima, dois 6 Ω resistors estão conectados em parallel. Portanto, a resistência equivalente entre D e E será de 3 Ω. Isso pode ser obtido fazendo a seguinte simplificação.

$$ R_ {DE} = \ frac {6 \ times 6} {6 + 6} = \ frac {36} {12} = 3 \ Omega $$

Na rede acima, os resistores 4 Ω e 8 Ω estão conectados em series. Portanto, a resistência equivalente entre F e G será de 12 Ω. Isso pode ser obtido fazendo a seguinte simplificação.

$$ R_ {FG} = 4 + 8 = 12 \ Omega $$

Step 2 - O elétrico simplificado network after Step 1 é mostrado na figura a seguir.

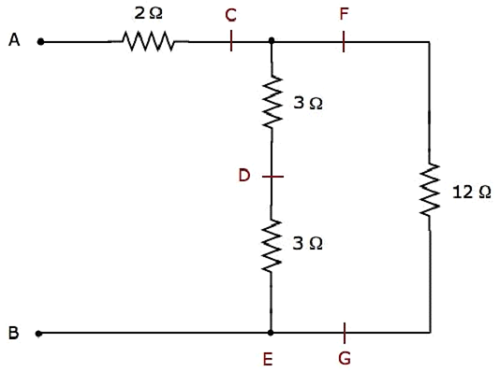
Na rede acima, dois 3 Ω resistors estão conectados em series. Portanto, a resistência equivalente entre C e E será6 Ω. Isso pode ser obtido fazendo a seguinte simplificação.

$$ R_ {CE} = 3 + 3 = 6 \ Omega $$

Step 3 - O elétrico simplificado network after Step 2 é mostrado na figura a seguir.

Na rede acima, os resistores 6 Ω e 12 Ω estão conectados em parallel. Portanto, a resistência equivalente entre C e B será de 4 Ω. Isso pode ser obtido fazendo a seguinte simplificação.

$$ R_ {CB} = \ frac {6 \ times 12} {6 + 12} = \ frac {72} {18} = 4 \ Omega $$

Step 4 - O elétrico simplificado network after Step 3 é mostrado na figura a seguir.

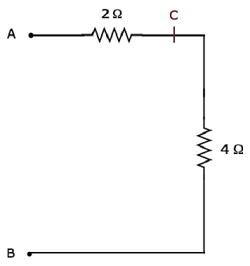
Na rede acima, os resistores 2 Ω e 4 Ω estão conectados em seriesentre os terminais A e B. Portanto, a resistência equivalente entre A e B será de 6 Ω. Isso pode ser obtido fazendo a seguinte simplificação.

$$ R_ {AB} = 2 + 4 = 6 \ Omega $$

Portanto, a resistência equivalente entre os terminais A e B da rede elétrica dada é 6 Ω.