Teoria da Rede - Leis de Kirchhoff
Os elementos da rede podem ser active ou passivetipo. Qualquer circuito ou rede elétrica contém um desses dois tipos de elementos de rede ou uma combinação de ambos.
Agora, vamos discutir sobre as duas leis a seguir, que são conhecidas popularmente como Kirchhoff’s laws.
- Lei Atual de Kirchhoff
- Lei de tensão de Kirchhoff
Lei Atual de Kirchhoff
A Lei Atual de Kirchhoff (KCL) afirma que a soma algébrica das correntes que saem (ou entram) em um nó é igual a zero.
UMA Nodeé um ponto onde dois ou mais elementos de circuito estão conectados a ele. Se apenas dois elementos de circuito estiverem conectados a um nó, ele será considerado um nó simples. Se três ou mais elementos de circuito estão conectados a um nó, então se diz que éPrincipal Node.
Mathematically, KCL pode ser representado como
$$ \ displaystyle \ sum \ limits_ {m = 1} ^ M I_m = 0 $$
Onde,
Imé a m- ésima corrente do ramo saindo do nó.
M é o número de ramos que estão conectados a um nó.
A declaração acima de KCLtambém pode ser expresso como "a soma algébrica das correntes que entram em um nó é igual à soma algébrica das correntes que saem de um nó". Vamos verificar essa afirmação por meio do exemplo a seguir.
Exemplo
Escreva KCL equation no nó P da figura a seguir.
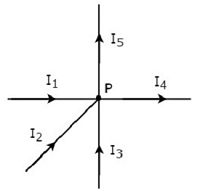
Na figura acima, as correntes do ramal I 1 , I 2 e I 3 sãoentering no nó P. Portanto, considere sinais negativos para essas três correntes.
Na figura acima, as correntes do ramal I 4 e I 5 sãoleaving do nó P. Portanto, considere sinais positivos para essas duas correntes.
o KCL equation no nó P será
$$ - I_1 - I_2 - I_3 + I_4 + I_5 = 0 $$
$$ \ Rightarrow I_1 + I_2 + I_3 = I_4 + I_5 $$
Na equação acima, o lado esquerdo representa a soma das correntes de entrada, enquanto o lado direito representa a soma das correntes de saída.
Neste tutorial, vamos considerar o sinal positivo quando a corrente sai de um nó e o sinal negativo quando entra em um nó. Da mesma forma, você pode considerar sinal negativo quando a corrente sai de um nó e sinal positivo quando entra em um nó. Em ambos os casos, oresult will be same.
Note - KCL é independente da natureza dos elementos da rede que estão conectados a um nó.
Lei de tensão de Kirchhoff
A Lei da Tensão de Kirchhoff (KVL) afirma que a soma algébrica das tensões em torno de um loop ou malha é igual a zero.
UMA Loopé um caminho que termina no mesmo nó de onde começou. Em contraste, umMesh é um loop que não contém nenhum outro loop dentro dele.
Matematicamente, KVL pode ser representado como
$$ \ displaystyle \ sum \ limits_ {n = 1} ^ N V_n = 0 $$
Onde,
Vné a tensão do enésimo elemento em um loop (malha).
N é o número de elementos de rede no loop (malha).
A declaração acima de KVLtambém pode ser expressa como "a soma algébrica das fontes de tensão é igual à soma algébrica das quedas de tensão que estão presentes em um loop." Vamos verificar essa afirmação com a ajuda do exemplo a seguir.
Exemplo
Escreva KVL equation em torno da volta do circuito seguinte.
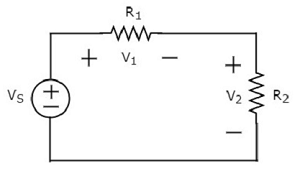
O diagrama de circuito acima consiste em uma fonte de tensão, V S em série com dois resistores R 1 e R 2 . As quedas de tensão nos resistores R 1 e R 2 são V 1 e V 2, respectivamente.
Aplique KVL em torno do loop.
$$ V_S - V_1 - V_2 = 0 $$
$$ \ Rightarrow V_S = V_1 + V_2 $$
Na equação acima, o termo do lado esquerdo representa uma única fonte de tensão VS. Considerando que, o lado direito representa osum of voltage drops. Neste exemplo, consideramos apenas uma fonte de tensão. É por isso que o lado esquerdo contém apenas um termo. Se considerarmos várias fontes de tensão, o lado esquerdo contém a soma das fontes de tensão.
Neste tutorial, consideramos o sinal da tensão de cada elemento como a polaridade do segundo terminal que está presente ao percorrer o loop. Da mesma forma, você pode considerar o sinal de cada tensão como a polaridade do primeiro terminal que está presente durante a viagem ao redor do loop. Em ambos os casos, oresult will be same.
Note - KVL é independente da natureza dos elementos da rede que estão presentes em um loop.