Teoria da Rede - Ressonância Paralela
No capítulo anterior, discutimos a importância da ressonância em série. Agora, vamos discutir a ressonância paralela em circuitos RLC.
Diagrama de Circuito de Ressonância Paralela
Se a ressonância ocorre em circuito RLC paralelo, é chamada de Parallel Resonance. Considere o seguinteparallel RLC circuit, que é representado no domínio fasorial.
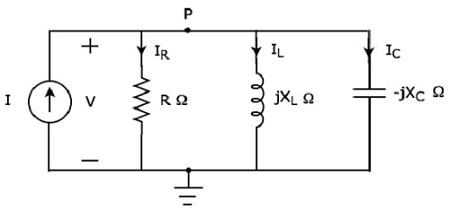
Aqui, os elementos passivos, como resistor, indutor e capacitor são conectados em paralelo. Esta combinação inteira está emparallel com a fonte de corrente senoidal de entrada.
Escreva nodal equation no nó P.
$$ - I + I_R + I_L + I_C = 0 $$
$$ \ Rightarrow - I + \ frac {V} {R} + \ frac {V} {j X_L} + \ frac {V} {- j X_C} = 0 $$
$$ \ Rightarrow I = \ frac {V} {R} - \ frac {jV} {X_L} + \ frac {jV} {X_C} $$
$ \ Rightarrow I = V [\ frac {1} {R} + j \ lgrupo \ frac {1} {X_C} - \ frac {1} {X_L} \ rgrupo] $Equation 1
A equação acima está na forma de I = VY.
Portanto, o admittance Y do circuito RLC paralelo será
$$ Y = \ frac {1} {R} + j \ lgrupo \ frac {1} {X_C} - \ frac {1} {X_L} \ rgrupo $$
Parâmetros e quantidades elétricas na ressonância
Agora, vamos derivar os valores dos parâmetros e grandezas elétricas na ressonância do circuito RLC paralelo, um por um.
Frequência de ressonância
Nós sabemos que o resonant frequency, fré a frequência com que ocorre a ressonância. Em paralelo ocorre a ressonância do circuito RLC, quando o termo imaginário de admitância, Y, é zero. ou seja, o valor de $ \ frac {1} {X_C} - \ frac {1} {X_L} $ deve ser igual a zero
$$ \ Rightarrow \ frac {1} {X_C} = \ frac {1} {X_L} $$
$$ \ Rightarrow X_L = X_C $$
A condição de ressonância acima é a mesma do circuito RLC em série. Então oresonant frequency, fr será o mesmo no circuito RLC em série e no circuito RLC paralelo.
Portanto, o resonant frequency, fr do circuito RLC paralelo é
$$ f_r = \ frac {1} {2 \ pi \ sqrt {LC}} $$
Onde,
- L é a indutância de um indutor.
- C é a capacitância de um capacitor.
o resonant frequency, fr do circuito RLC paralelo depende apenas da indutância L e capacitância C. Mas, é independente de resistênciaR.
Admissão
Nós temos o admittance Y de circuito RLC paralelo como
$$ Y = \ frac {1} {R} + j \ lgrupo \ frac {1} {X_C} - \ frac {1} {X_L} \ rgrupo $$
Substitua, $ X_L = X_C $ na equação acima.
$$ Y = \ frac {1} {R} + j \ lgrupo \ frac {1} {X_C} - \ frac {1} {X_C} \ rgrupo $$
$$ \ Rightarrow Y = \ frac {1} {R} + j (0) $$
$$ \ Rightarrow Y = \ frac {1} {R} $$
Na ressonância, o admittance, Y do circuito RLC paralelo é igual ao recíproco da resistência, R. ie, $ \ mathbf {\ mathit {Y = \ frac {1} {R}}} $
Tensão em cada elemento
Substitua, $ \ frac {1} {X_C} - \ frac {1} {X_L} = 0 $ na Equação 1
$$ I = V [\ frac {1} {R} + j (0)] $$
$$ \ Rightarrow I = \ frac {V} {R} $$
$$ \ Rightarrow V = IR $$
Portanto, o voltage em todos os elementos do circuito RLC paralelo em ressonância é V = IR.
Na ressonância, a admitância do circuito RLC paralelo atinge o valor mínimo. Conseqüentemente,maximum voltage está presente em cada elemento deste circuito em ressonância.
Corrente fluindo através do resistor
A corrente fluindo através do resistor é
$$ I_R = \ frac {V} {R} $$
Substitua o valor de V na equação acima.
$$ I_R = \ frac {IR} {R} $$
$$ \ Rightarrow I_R = I $$
Portanto, o current flowing through resistor na ressonância está $ \ mathbf {\ mathit {I_R = I}} $.
Corrente fluindo através do indutor
A corrente fluindo através do indutor é
$$ I_L = \ frac {V} {j X_L} $$
Substitua o valor de V na equação acima.
$$ I_L = \ frac {IR} {j X_L} $$
$$ \ Rightarrow I_L = -j \ lgrupo \ frac {R} {X_L} \ rgrupo I $$
$$ \ Rightarrow I_L = -jQI $$
Portanto, o current flowing through inductor na ressonância é $ I_L = -jQI $.
Então o magnitude da corrente fluindo através do indutor na ressonância será
$$ | I_L | = QI $$
Onde, Q é o Quality factor e seu valor é igual a $ \ frac {R} {X_L} $
Corrente fluindo através do capacitor
A corrente fluindo através do capacitor é
$$ I_C = \ frac {V} {- j X_C} $$
Substitua o valor de V na equação acima.
$$ I_C = \ frac {IR} {- j X_C} $$
$$ \ Rightarrow I_C = j \ lgrupo \ frac {R} {X_C} \ rgrupo I $$
$$ \ Rightarrow I_C = jQI $$
Portanto, o current flowing through capacitor na ressonância é $ I_C = jQI $
Então o magnitude da corrente fluindo através do capacitor na ressonância será
$$ | I_C | = QI $$
Onde, Q é o Quality factor e seu valor é igual a $ \ frac {R} {X_C} $
Note - O circuito RLC de ressonância paralela é chamado de current magnificationo circuito. Porque, a magnitude da corrente que flui através do indutor e capacitor é igual a Q vezes a entrada de corrente sinusoidal I .