Teoria da Rede - Teorema da Superposição
Superposition theorembaseia-se no conceito de linearidade entre a resposta e a excitação de um circuito elétrico. Ele afirma que a resposta em um determinado ramo de um circuito linear quando várias fontes independentes estão agindo ao mesmo tempo é equivalente à soma das respostas devido a cada fonte independente agindo em um momento.
Neste método, vamos considerar apenas one independent sourcede uma vez. Portanto, temos que eliminar as fontes independentes restantes do circuito. Podemos eliminar as fontes de tensão colocando em curto seus dois terminais e, da mesma forma, as fontes de corrente abrindo seus dois terminais.
Portanto, precisamos encontrar a resposta em um determinado ramo ‘n’ timesse houver 'n' fontes independentes. A resposta em uma ramificação específica pode ser corrente fluindo através dessa ramificação ou tensão através dessa ramificação.
Procedimento do Teorema da Superposição
Siga estas etapas para encontrar a resposta em um ramo particular usando o teorema da superposição.
Step 1 - Encontre a resposta em um determinado ramo, considerando uma fonte independente e eliminando as fontes independentes restantes presentes na rede.
Step 2 - Repita a Etapa 1 para todas as fontes independentes presentes na rede.
Step 3 - Adicione todas as respostas para obter a resposta geral em um determinado ramo quando todas as fontes independentes estiverem presentes na rede.
Exemplo
Encontre a corrente fluindo através do resistor de 20 Ω do seguinte circuito usando superposition theorem.
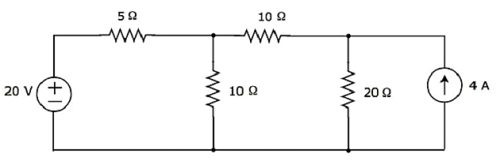
Step 1 - Vamos encontrar a corrente fluindo através do resistor de 20 Ω considerando apenas 20 V voltage source. Neste caso, podemos eliminar a fonte de corrente de 4 A abrindo-a em circuito. O diagrama de circuito modificado é mostrado na figura a seguir.

Há apenas um nó principal, exceto aterramento no circuito acima. Então, podemos usarnodal analysismétodo. A tensão do nó V 1 é rotulada na figura a seguir. Aqui, V 1 é a tensão do nó 1 em relação ao terra.
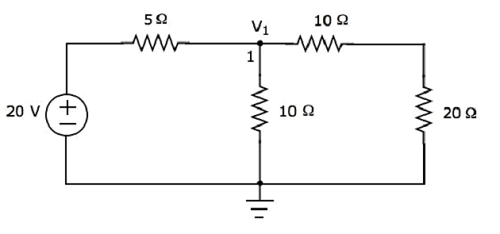
o nodal equation no nó 1 é
$$ \ frac {V_1 - 20} {5} + \ frac {V_1} {10} + \ frac {V_1} {10 + 20} = 0 $$
$$ \ Rightarrow \ frac {6V_1 - 120 + 3V_1 + V_1} {30} = 0 $$
$$ \ Rightarrow 10V_1 = 120 $$
$$ \ Rightarrow V_1 = 12V $$
o current flowing through 20 Ω resistor pode ser encontrado fazendo a seguinte simplificação.
$$ I_1 = \ frac {V_1} {10 + 20} $$
Substitua o valor de V 1 na equação acima.
$$ I_1 = \ frac {12} {10 + 20} = \ frac {12} {30} = 0,4 A $$
Portanto, a corrente que flui através do resistor de 20 Ω é 0.4 A, quando apenas a fonte de tensão de 20 V é considerada.
Step 2 - Vamos encontrar a corrente fluindo através do resistor de 20 Ω considerando apenas 4 A current source. Neste caso, podemos eliminar a fonte de tensão de 20 V fazendo um curto-circuito dela. O diagrama de circuito modificado é mostrado na figura a seguir.
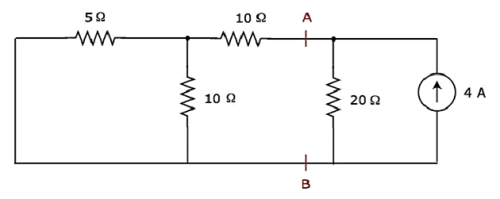
No circuito acima, existem três resistores à esquerda dos terminais A e B. Podemos substituir esses resistores por um único equivalent resistor. Aqui, os resistores de 5 Ω e 10 are são conectados em paralelo e toda a combinação está em série com o resistor de 10 Ω.
o equivalent resistance à esquerda dos terminais A e B estará
$$ R_ {AB} = \ lgrupo \ frac {5 \ vezes 10} {5 + 10} \ rgrupo + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega $$
O diagrama de circuito simplificado é mostrado na figura a seguir.
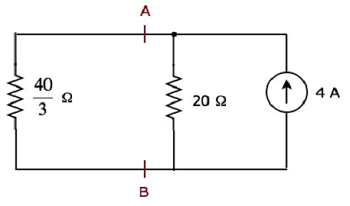
Podemos encontrar a corrente fluindo através do resistor de 20 Ω, usando current division principle.
$$ I_2 = I_S \ lgrupo \ frac {R_1} {R_1 + R_2} \ rgrupo $$
Substitua $ I_S = 4A, \: R_1 = \ frac {40} {3} \ Omega $ e $ R_2 = 20 \ Omega $ na equação acima.
$$ I_2 = 4 \ lgrupo \ frac {\ frac {40} {3}} {\ frac {40} {3} + 20} \ rgrupo = 4 \ lgrupo \ frac {40} {100} \ rgrupo = 1,6 A $$
Portanto, a corrente que flui através do resistor de 20 Ω é 1.6 A, quando apenas 4 A fonte de corrente é considerada.
Step 3 - Obteremos a corrente fluindo através do resistor de 20 Ω do circuito dado, fazendo o addition of two currents que obtivemos na etapa 1 e etapa 2. Matematicamente, pode ser escrito como
$$ I = I_1 + I_2 $$
Substitua os valores de I 1 e I 2 na equação acima.
$$ I = 0,4 + 1,6 = 2 A $$
Portanto, a corrente que flui através do resistor de 20 Ω de determinado circuito é 2 A.
Note - Não podemos aplicar o teorema da superposição diretamente para encontrar a quantidade de powerentregue a qualquer resistor que esteja presente em um circuito linear, bastando fazer a soma das potências entregues a esse resistor devido a cada fonte independente. Em vez disso, podemos calcular a corrente total fluindo ou a tensão através desse resistor usando o teorema da superposição e, a partir disso, podemos calcular a quantidade de potência fornecida a esse resistor usando $ I ^ 2 R $ ou $ \ frac {V ^ 2} {R}$.