Teoria de Rede - Circuitos Equivalentes
Se um circuito consiste em dois ou mais elementos passivos semelhantes e são conectados exclusivamente do tipo série ou tipo paralelo, então podemos substituí-los por um único elemento passivo equivalente. Portanto, este circuito é chamado deequivalent circuit.
Neste capítulo, vamos discutir sobre os dois circuitos equivalentes a seguir.
- Circuito Equivalente em Série
- Circuito Equivalente Paralelo
Circuito Equivalente em Série
Se elementos passivos semelhantes estiverem conectados em series, então a mesma corrente fluirá por todos esses elementos. Mas, a voltagem é dividida em cada elemento.
Considere o seguinte circuit diagram.
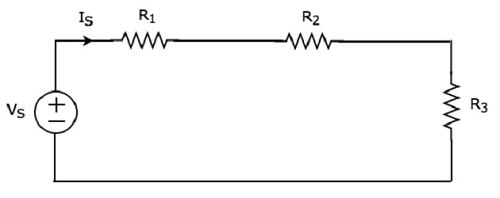
Ele tem uma única fonte de tensão (V S ) e três resistores com resistências de R 1 , R 2 e R 3 . Todos esses elementos estão conectados em série. O IS atual flui por todos esses elementos.
O circuito acima possui apenas uma malha. oKVL equation em torno desta malha é
$$ V_S = V_1 + V_2 + V_3 $$
Substitua $ V_1 = I_S R_1, \: V_2 = I_S R_2 $ e $ V_3 = I_S R_3 $ na equação acima.
$$ V_S = I_S R_1 + I_S R_2 + I_S R_3 $$
$$ \ Rightarrow V_S = I_S (R_1 + R_2 + R_3) $$
A equação acima está na forma de $ V_S = I_S R_ {Eq} $ onde,
$$ R_ {Eq} = R_1 + R_2 + R_3 $$
o equivalent circuit diagram do circuito fornecido é mostrado na figura a seguir.
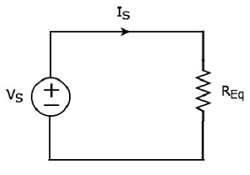
Isso significa que, se vários resistores estiverem conectados em série, podemos substituí-los por um equivalent resistor. A resistência deste resistor equivalente é igual à soma das resistências de todos aqueles resistores múltiplos.
Note 1- Se indutores 'N' tendo indutâncias de L 1 , L 2 , ..., L N estiverem conectados em série, então oequivalent inductance será
$$ L_ {Eq} = L_1 + L_2 + ... + L_N $$
Note 2- Se 'N' capacitores com capacitâncias de C 1 , C 2 , ..., C N estiverem conectados em série, então oequivalent capacitance será
$$ \ frac {1} {C_ {Eq}} = \ frac {1} {C_1} + \ frac {1} {C_2} + ... + \ frac {1} {C_N} $$
Circuito Equivalente Paralelo
Se elementos passivos semelhantes estiverem conectados em parallel, então a mesma voltagem será mantida em cada elemento. Mas, a corrente que flui através de cada elemento é dividida.
Considere o seguinte circuit diagram.

Ele tem uma única fonte de corrente (I S ) e três resistores com resistências de R 1 , R 2 e R 3 . Todos esses elementos estão conectados em paralelo. A tensão (V S ) está disponível em todos esses elementos.
O circuito acima tem apenas um nó principal (P), exceto o nó Terra. oKCL equation neste nó principal (P) é
$$ I_S = I_1 + I_2 + I_3 $$
Substitua $ I_1 = \ frac {V_S} {R_1}, \: I_2 = \ frac {V_S} {R_2} $ e $ I_3 = \ frac {V_S} {R_3} $ na equação acima.
$$ I_S = \ frac {V_S} {R_1} + \ frac {V_S} {R_2} + \ frac {V_S} {R_3} $$
$$ \ Rightarrow I_S = V_S \ lgrupo \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgrupo $$
$$ \ Rightarrow V_S = I_S \ left [\ frac {1} {\ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup} \ right] $$
A equação acima está na forma de V S = I S R Eq , onde,
$$ R_ {Eq} = \ frac {1} {\ lgrupo \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgrupo} $$
$$ \ frac {1} {R_ {Eq}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} $$
o equivalent circuit diagram do circuito fornecido é mostrado na figura a seguir.
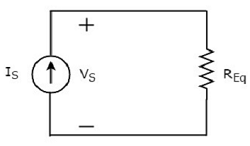
Isso significa que, se vários resistores estiverem conectados em paralelo, podemos substituí-los por um resistor equivalente. A resistência desteequivalent resistor é igual ao recíproco da soma do recíproco de cada resistência de todas aquelas resistências múltiplas.
Note 1- Se indutores 'N' com indutâncias de L 1 , L 2 , ..., L N estiverem conectados em paralelo, então oequivalent inductance será
$$ \ frac {1} {L_ {Eq}} = \ frac {1} {L_1} + \ frac {1} {L_2} + ... + \ frac {1} {L_N} $$
Note 2- Se 'N' capacitores com capacitâncias de C 1 , C 2 , ..., C N estiverem conectados em paralelo, então oequivalent capacitance será
$$ C_ {Eq} = C_1 + C_2 + ... + C_N $$