Teoria da Rede - Topologia da Rede
A topologia de rede é uma representação gráfica de circuitos elétricos. É útil para analisar circuitos elétricos complexos, convertendo-os em gráficos de rede. A topologia de rede também é chamada deGraph theory.
Terminologia Básica da Topologia de Rede
Agora, vamos discutir sobre a terminologia básica envolvida nesta topologia de rede.
Gráfico
O gráfico da rede é simplesmente chamado de graph. Consiste em um conjunto de nós conectados por ramos. Nos gráficos, um nó é um ponto comum de dois ou mais ramos. Às vezes, apenas uma única ramificação pode se conectar ao nó. Uma ramificação é um segmento de linha que conecta dois nós.
Qualquer circuito elétrico ou rede pode ser convertido em seu equivalente graphsubstituindo os elementos passivos e as fontes de tensão por curto-circuitos e as fontes de corrente por circuitos abertos. Isso significa que os segmentos de linha no gráfico representam os ramos correspondentes a elementos passivos ou fontes de tensão do circuito elétrico.
Exemplo
Vamos considerar o seguinte electric circuit.
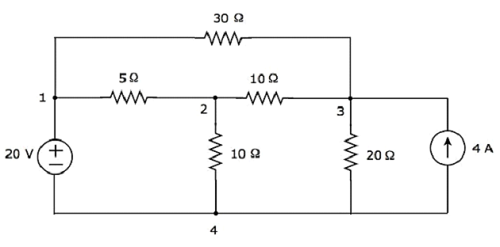
No circuito acima, existem four principal nodes e aqueles são rotulados com 1, 2, 3 e 4. Existem seven branches no circuito acima, entre o qual uma ramificação contém uma fonte de tensão de 20 V, outra ramificação contém uma fonte de corrente de 4 A e as cinco ramificações restantes contêm resistências com resistências de 30 Ω, 5 Ω, 10 Ω, 10 Ω e 20 Ω respectivamente.
Um equivalente graph correspondente ao circuito elétrico acima é mostrado na figura a seguir.
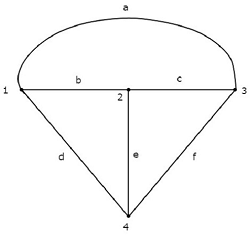
No gráfico acima, existem four nodese aqueles são rotulados com 1, 2, 3 e 4 respectivamente. Estes são os mesmos dos nós principais do circuito elétrico. temsix branches no gráfico acima e aqueles são rotulados com a, b, c, d, e e f respectivamente.
Neste caso, temos one branch less no gráfico porque a fonte de corrente de 4 A é feita como circuito aberto, enquanto converte o circuito elétrico em seu gráfico equivalente.
A partir deste exemplo, podemos concluir os seguintes pontos -
o number of nodes presente em um grafo será igual ao número de nós principais presentes em um circuito elétrico.
o number of branches presente em um gráfico será menor ou igual ao número de ramos presentes em um circuito elétrico.
Tipos de gráficos
A seguir estão os tipos de gráficos -
- Gráfico Conectado
- Gráfico Desconectado
- Gráfico Direcionado
- Gráfico não direcionado
Agora, vamos discutir esses gráficos um por um.
Gráfico Conectado
Se houver pelo menos um ramo entre qualquer um dos dois nós de um gráfico, ele é chamado de connected graph. Isso significa que cada nó do grafo conectado terá uma ou mais ramificações conectadas a ele. Portanto, nenhum nó será apresentado como isolado ou separado.
O gráfico mostrado no exemplo anterior é um connected graph. Aqui, todos os nós são conectados por três ramos.
Gráfico Desconectado
Se houver pelo menos um nó no gráfico que permanece desconectado, mesmo por um único ramo, ele é chamado de unconnected graph. Portanto, haverá um ou mais nós isolados em um grafo não conectado.
Considere o gráfico mostrado na figura a seguir.
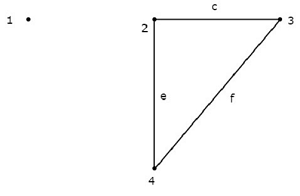
Neste gráfico, os nós 2, 3 e 4 são conectados por dois ramos cada. Mas, nem mesmo um único ramo foi conectado aonode 1. Então, o nó 1 se torna umisolated node. Portanto, o gráfico acima é umunconnected graph.
Gráfico Direcionado
Se todos os ramos de um gráfico são representados com setas, então esse gráfico é chamado de directed graph. Essas setas indicam a direção do fluxo de corrente em cada ramo. Portanto, este gráfico também é chamado deoriented graph.
Considere o gráfico mostrado na figura a seguir.
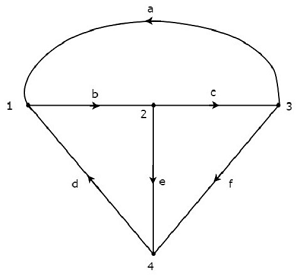
No gráfico acima, a direção do fluxo da corrente é representada por uma seta em cada ramo. Portanto, é umdirected graph.
Gráfico não direcionado
Se os ramos de um gráfico não são representados com setas, então esse gráfico é chamado de undirected graph. Uma vez que não há direções de fluxo de corrente, este gráfico também é chamado deunoriented graph.
O gráfico que foi mostrado no primeiro exemplo deste capítulo é um unoriented graph, porque não há setas nas ramificações desse gráfico.
Subgrafo e seus tipos
Uma parte do gráfico é chamada de subgraph. Obtemos subgráficos removendo alguns nós e / ou ramos de um determinado gráfico. Assim, o número de ramos e / ou nós de um subgráfico será menor do que o do gráfico original. Portanto, podemos concluir que um subgráfico é um subconjunto de um gráfico.
A seguir estão os two types de subgráficos.
- Tree
- Co-Tree
Árvore
Árvore é um subgráfico conectado de um determinado gráfico, que contém todos os nós de um gráfico. Mas, não deve haver nenhum loop nesse subgráfico. Os ramos de uma árvore são chamados detwigs.
Considere o seguinte connected subgraph do gráfico, que é mostrado no Exemplo do início deste capítulo.
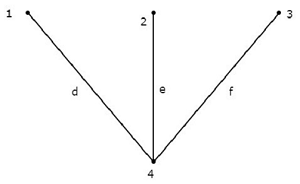
Este subgráfico conectado contém todos os quatro nós do gráfico dado e não há nenhum loop. Portanto, é umTree.
Esta Árvore tem apenas três ramos de seis ramos de determinado gráfico. Porque, se considerarmos até mesmo um único ramo dos ramos restantes do gráfico, haverá um loop no subgrafo conectado acima. Então, o subgrafo conectado resultante não será uma Árvore.
A partir da árvore acima, podemos concluir que o number of branches que estão presentes em uma árvore devem ser iguais a n - 1 onde 'n' é o número de nós do grafo fornecido.
Co-Tree
Co-Tree é um subgrafo, que é formado com os ramos que são removidos durante a formação de uma Árvore. Portanto, é chamado deComplementde uma árvore. Para cada árvore, haverá uma co-árvore correspondente e seus ramos são chamados delinksou acordes. Em geral, os links são representados por linhas pontilhadas.
o Co-Tree correspondente à Árvore acima é mostrada na figura a seguir.
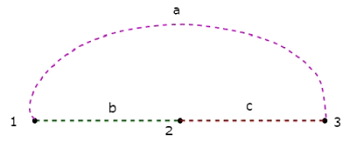
Esta co-árvore tem apenas três nós em vez de quatro nós do gráfico fornecido, porque o nó 4 está isolado da co-árvore acima. Portanto, a Co-Tree não precisa ser um subgrafo conectado. Esta co-árvore tem três ramos e eles formam um loop.
o number of branchesque estão presentes em uma co-árvore será igual à diferença entre o número de ramos de um determinado gráfico e o número de ramos. Matematicamente, pode ser escrito como
$$ l = b - (n - 1) $$
$$ l = b - n + 1 $$
Onde,
- l é o número de links.
- b é o número de ramos presentes em um determinado gráfico.
- n é o número de nós presentes em um determinado gráfico.
Se combinarmos uma árvore e sua co-árvore correspondente, obteremos o original graph como mostrado abaixo.
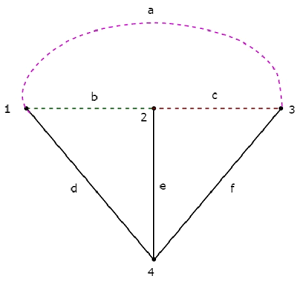
Os ramos da árvore d, e e f são representados por linhas sólidas. Os ramos a, b e c da Co-Tree são representados por linhas tracejadas.