Teoria de Rede - Resposta de Circuitos DC
Se a saída de um circuito elétrico para uma entrada varia em relação ao tempo, é chamada de time response. O tempo de resposta consiste em duas partes.
- Resposta transitória
- Resposta de estado estacionário
Neste capítulo, primeiro vamos discutir sobre essas duas respostas e, em seguida, observar essas duas respostas em um circuito RL série, quando é excitado por uma fonte de tensão CC.
Resposta transitória
Depois de aplicar uma entrada a um circuito elétrico, a saída leva certo tempo para atingir o estado estacionário. Portanto, a saída estará em estado transiente até que vá para um estado estável. Portanto, a resposta do circuito elétrico durante o estado transiente é conhecida comotransient response.
A resposta transitória será zero para grandes valores de 't'. Idealmente, esse valor de 't' deve ser infinito. Mas, praticamentefive time constants são suficientes.
Presença ou Ausência de Transientes
Transientes ocorrem na resposta devido a sudden changenas fontes que são aplicadas ao circuito elétrico e / ou por ação de chaveamento. Existem duas ações de comutação possíveis. Essas são a chave de abertura e a chave de fechamento.
o transient parte vai not presentna resposta de um circuito elétrico ou rede, se contiver apenas resistências. Porqueresistor é ter a capacidade de ajustar qualquer quantidade de tensão e corrente.
o transient part occurs na resposta de um circuito elétrico ou rede devido à presença de elementos de armazenamento de energia, como inductor and capacitor. Porque eles não podem alterar a energia armazenada nesses elementos instantaneamente.
Comportamento do Indutor
Suponha que a ação de comutação ocorra em t = 0.Inductor currentnão muda instantaneamente, quando a ação de comutação ocorre. Isso significa que o valor da corrente do indutor logo após a ação de comutação será o mesmo que antes da ação de comutação.
Matematicamente, pode ser representado como
$$ i_L (0 ^ +) = i_L (0 ^ -) $$
Comportamento do capacitor
o capacitor voltagenão muda instantaneamente de forma semelhante à corrente do indutor, quando a ação de comutação ocorre. Isso significa que o valor da tensão do capacitor logo após a ação de comutação será o mesmo que antes da ação de comutação.
Matematicamente, pode ser representado como
$$ v_c (0 ^ +) = v_c (0 ^ -) $$
Resposta de estado estacionário
A parte da resposta de tempo que permanece mesmo depois que a resposta transitória tornou-se o valor zero para grandes valores de 't' é conhecida como steady state response. Isso significa que não haverá nenhuma parte transitória na resposta durante o estado estacionário.
Comportamento do Indutor
Se a fonte independente for conectada ao circuito elétrico ou rede tendo um ou mais indutores e resistores (opcional) por um longo tempo, então esse circuito elétrico ou rede é dito estar em estado estacionário. Portanto, a energia armazenada no (s) indutor (es) desse circuito elétrico é de máxima e constante.
Matematicamente, pode ser representado como
$ W_L = \ frac {L {i_L} ^ 2} {2} = $ Máximo e constante
$ \ Rightarrow i_L = $ Máximo e constante
Portanto, o indutor atua como um constant current source em estado estacionário.
A tensão no indutor será
$$ V_L = L \ frac {di_ {L}} {dt} = 0V $$
Então, o indutor atua como um short circuit em estado estacionário.
Comportamento do capacitor
Se a fonte independente for conectada ao circuito elétrico ou rede tendo um ou mais capacitores e resistores (opcional) por um longo tempo, então esse circuito elétrico ou rede é dito estar em estado estacionário. Portanto, a energia armazenada no (s) capacitor (es) desse circuito elétrico é de máxima e constante.
Matematicamente, pode ser representado como
$ W_c = \ frac {C {v_c} ^ 2} {2} = $ Máximo e constante
$ \ Rightarrow v_c = $ Máximo e constante
Portanto, o capacitor atua como um constant voltage source em estado estacionário.
A corrente que flui através do capacitor será
$$ i_c = C \ frac {dv_c} {dt} = 0A $$
Então, o capacitor atua como um open circuit em estado estacionário.
Encontrando a Resposta do Circuito Série RL
Considere o seguinte series RL circuit diagrama.
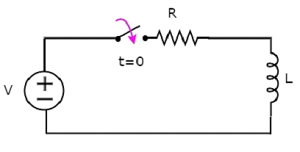
No circuito acima, o switch foi mantido openaté t = 0 e foi fechado em t = 0. Assim, a fonte de tensão DC com V volts não está conectada ao circuito em série RL até este momento. Portanto, existeno initial current flui através do indutor.
O diagrama de circuito, quando o switch é em closed posição é mostrada na figura a seguir.
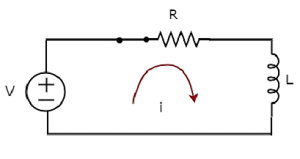
Agora, o atual i flui em todo o circuito, uma vez que a fonte de tensão DC tendo V volts está conectado ao circuito série RL.
Agora, aplique KVL em torno do loop.
$$ V = Ri + L \ frac {di} {dt} $$
$ \ frac {di} {dt} + \ lgroup \ frac {R} {L} \ rgroup i = \ frac {V} {L} $Equation 1
A equação acima é uma equação diferencial de primeira ordem e está na forma de
$ \ frac {dy} {dt} + Py = Q $Equation 2
De comparing Equação 1 e Equação 2, obteremos as seguintes relações.
$$ x = t $$
$$ y = i $$
$$ P = \ frac {R} {L} $$
$$ Q = \ frac {V} {L} $$
o solution da Equação 2 será
$ ye ^ {\ int p dx} = \ int Q e ^ {\ int p dx} dx + k $Equation 3
Onde, k é a constante.
Substitua os valores de x, y, P e Q na Equação 3.
$ ie ^ {\ int {\ lgrupo \ frac {R} {L} \ rgrupo} dt} = \ int (\ frac {V} {L}) \ lgrupo e ^ {\ int {\ lgrupo \ frac {R} {L} \ rgroup} dt} \ rgroup dt + k $
$ \ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ int e ^ {\ lgroup \ frac {R} {L} \ rgroup t} dt + k $
$ \ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ lbrace \ frac {e ^ {\ lgroup \ frac {R} {L} \ rgroup} t} {\ frac {R} {L}} \ rbrace + k $
$ \ Rightarrow i = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup} t $Equation 4
Sabemos que não há corrente inicial no circuito. Portanto, substitua, t = 0 e = 0 na Equação 4, a fim de encontrar o valor da constante k.
$$ 0 = \ frac {V} {R} + ke ^ {- \ lgrupo \ frac {R} {L} \ rgrupo (0)} $$
$$ 0 = \ frac {V} {R} + k (1) $$
$$ k = - \ frac {V} {R} $$
Substitua o valor de k na Equação 4.
$$ i = \ frac {V} {R} + \ lgrupo - \ frac {V} {R} \ rgrupo e ^ {- \ lgrupo \ frac {R} {L} \ rgrupo t} $$
$$ i = \ frac {V} {R} - \ frac {V} {R} e ^ {- \ lgrupo \ frac {R} {L} \ rgrupo t} $$
Portanto, o current fluindo através do circuito é
$ i = - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} + \ frac {V} {R} $Equation 5
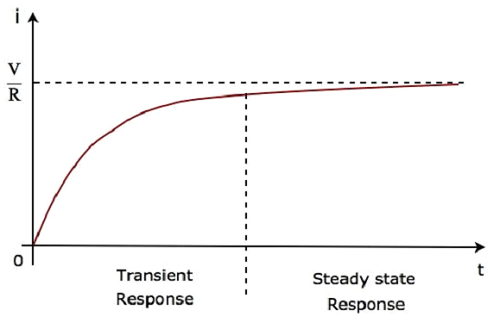
Portanto, a resposta do circuito em série RL, quando excitado por uma fonte de tensão CC, possui os dois termos a seguir.
O primeiro termo $ - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $ corresponde com o transient response.
O segundo termo $ \ frac {V} {R} $ corresponde ao steady state response. Essas duas respostas são mostradas na figura a seguir.
Podemos reescrever a Equação 5 da seguinte forma -
$ i = \ frac {V} {R} \ lgrupo 1 - e ^ {- \ lgrupo \ frac {R} {L} \ rgrupo t} \ rgrupo $
$ \ Rightarrow i = \ frac {V} {R} \ lgrupo 1 - e ^ {- \ lgrupo \ frac {t} {\ tau} \ rgrupo} \ rgrupo $Equation 6
Onde, τ é o time constant e seu valor é igual a $ \ frac {L} {R} $.
Ambas as Equações 5 e 6 são iguais. Mas, podemos compreender facilmente a forma de onda acima da corrente fluindo através do circuito da Equação 6, substituindo alguns valores det como 0, τ, 2τ, 5τ, etc.
Na forma de onda acima da corrente fluindo através do circuito, a resposta transitória apresentará até cinco constantes de tempo a partir de zero, enquanto a resposta em regime permanente apresentará a partir de cinco constantes de tempo.