Teoria da Rede - Ressonância em Série
Resonanceocorre em circuitos elétricos devido à presença de elementos de armazenamento de energia como indutor e capacitor. É o conceito fundamental com base no qual os receptores de rádio e TV são projetados de tal forma que devem ser capazes de selecionar apenas a freqüência da estação desejada.
tem two typesde ressonâncias, nomeadamente ressonância em série e ressonância paralela. Eles são classificados com base nos elementos da rede que estão conectados em série ou em paralelo. Neste capítulo, vamos discutir sobre a ressonância em série.
Diagrama de circuito de ressonância em série
Se a ressonância ocorre no circuito RLC em série, é chamada de Series Resonance. Considere o seguinteseries RLC circuit, que é representado no domínio fasorial.
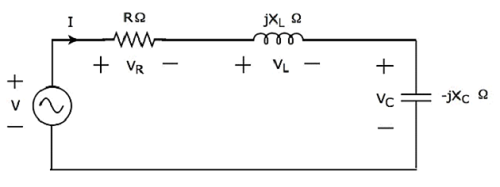
Aqui, os elementos passivos como resistor, indutor e capacitor são conectados em série. Esta combinação inteira está emseries com a fonte de tensão sinusoidal de entrada.
Aplique KVL em torno do loop.
$$ V - V_R - V_L - V_C = 0 $$
$$ \ Rightarrow V - IR - I (j X_L) - I (-j X_C) = 0 $$
$$ \ Rightarrow V = IR + I (j X_L) + I (-j X_C) $$
$ \ Rightarrow V = I [R + j (X_L - X_C)] $Equation 1
A equação acima está na forma de V = IZ.
Portanto, o impedance Z da série RLC circuito será
$$ Z = R + j (X_L - X_C) $$
Parâmetros e quantidades elétricas na ressonância
Agora, vamos derivar os valores dos parâmetros e grandezas elétricas na ressonância do circuito RLC em série, um por um.
Frequência de ressonância
A frequência em que ocorre a ressonância é chamada de resonant frequency fr. Na série RLC ocorre a ressonância do circuito, quando o termo imaginário da impedância Z é zero, ou seja, o valor de $ X_L - X_C $ deve ser igual a zero.
$$ \ Rightarrow X_L = X_C $$
Substitua $ X_L = 2 \ pi f L $ e $ X_C = \ frac {1} {2 \ pi f C} $ na equação acima.
$$ 2 \ pi f L = \ frac {1} {2 \ pi f C} $$
$$ \ Rightarrow f ^ 2 = \ frac {1} {(2 \ pi) ^ 2 LC} $$
$$ \ Rightarrow f = \ frac {1} {(2 \ pi) \ sqrt {LC}} $$
Portanto, o resonant frequency fr da série RLC circuito é
$$ f_r = \ frac {1} {(2 \ pi) \ sqrt {LC}} $$
Onde, L é a indutância de um indutor e C é a capacitância de um capacitor.
o resonant frequency fr do circuito RLC série depende apenas da indutância L e capacitância C. Mas, é independente de resistênciaR.
Impedância
Nós temos o impedance Z do circuito RLC série como
$$ Z = R + j (X_L - X_C) $$
Substitua $ X_L = X_C $ na equação acima.
$$ Z = R + j (X_C - X_C) $$
$$ \ Rightarrow Z = R + j (0) $$
$$ \ Rightarrow Z = R $$
Na ressonância, o impedance Z da série RLC circuito é igual ao valor da resistência R, ou seja, Z = R.
Corrente fluindo através do circuito
Substitua $ X_L - X_C = 0 $ na Equação 1.
$$ V = I [R + j (0)] $$
$$ \ Rightarrow V = IR $$
$$ \ Rightarrow I = \ frac {V} {R} $$
Portanto, current fluindo através do circuito RLC em série em ressonância é $ \ mathbf {\ mathit {I = \ frac {V} {R}}} $.
Na ressonância, a impedância do circuito RLC em série atinge o valor mínimo. Portanto, omaximum current flui através deste circuito em ressonância.
Tensão no resistor
A tensão no resistor é
$$ V_R = IR $$
Substitua o valor de I na equação acima.
$$ V_R = \ lgrupo \ frac {V} {R} \ rgrupo R $$
$$ \ Rightarrow V_R = V $$
Portanto, o voltage across resistor em ressonância é VR = V.
Tensão através do indutor
A tensão através do indutor é
$$ V_L = I (jX_L) $$
Substitua o valor de I na equação acima.
$$ V_L = \ lgrupo \ frac {V} {R} \ rgrupo (jX_L) $$
$$ \ Rightarrow V_L = j \ lgrupo \ frac {X_L} {R} \ rgrupo V $$
$$ \ Rightarrow V_L = j QV $$
Portanto, o voltage across inductor em ressonância é $ V_L = j QV $.
Então o magnitude de tensão através do indutor na ressonância será
$$ | V_L | = QV $$
Onde Q é o Quality factor e seu valor é igual a $ \ frac {X_L} {R} $
Tensão através do capacitor
A tensão no capacitor é
$$ V_C = I (-j X_C) $$
Substitua o valor de I na equação acima.
$$ V_C = \ lgrupo \ frac {V} {R} \ rgrupo (-j X_C) $$
$$ \ Rightarrow V_C = -j \ lgrupo \ frac {X_C} {R} \ rgrupo V $$
$$ \ Rightarrow V_C = -jQV $$
Portanto, o voltage across capacitor na ressonância está $ \ mathbf {\ mathit {V_C = -jQV}} $.
Então o magnitude de tensão através do capacitor na ressonância será
$$ | V_C | = QV $$
Onde Q é o Quality factor e seu valor é igual a $ \ frac {X_ {C}} {R} $
Note - O circuito RLC de ressonância em série é chamado de voltage magnificationcircuito, porque a magnitude da tensão através do indutor e o capacitor é igual a Q vezes a entrada de tensão sinusoidal V .