Teoria de Rede - Resposta de Circuitos AC
No capítulo anterior, discutimos a resposta transiente e a resposta de estado estacionário do circuito CC. Neste capítulo, vamos discutir oresponse of AC circuit. Os conceitos de resposta transiente e resposta de estado estacionário, que discutimos no capítulo anterior, também serão úteis aqui.
Encontrando a Resposta do Circuito Série RL
Considere o seguinte series RL circuit diagrama.

No circuito acima, o switch foi mantido openaté t = 0 e foi fechado em t = 0 . Portanto, a fonte de tensão CA com uma tensão de pico de V m volts não está conectada ao circuito em série RL até este momento. Portanto, existeno initial current flui através do indutor.
O diagrama de circuito, quando o switch é em closed posição, é mostrado na figura a seguir.
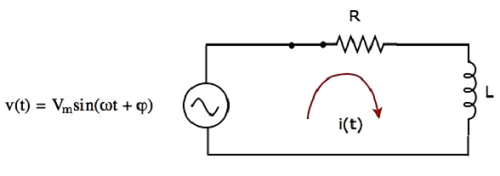
Agora, a corrente i (t) flui em todo o circuito, uma vez que a fonte de tensão CA com uma tensão de pico de V m volts está conectada ao circuito série RL.
Sabemos que a corrente i (t) fluindo através do circuito acima terá dois termos, um que representa a parte transitória e outro termo representa o estado estacionário.
Matematicamente, pode ser representado como
$ i (t) = i_ {Tr} (t) + i_ {ss} (t) $Equation 1
Onde,
$ i_ {Tr} (t) $ é a resposta transitória da corrente que flui pelo circuito.
$ i_ {ss} (t) $ é a resposta em regime permanente da corrente fluindo através do circuito.
No capítulo anterior, obtivemos a resposta transitória da corrente fluindo através do circuito da série RL. Ele está na forma de $ Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} $.
Substitua $ i_ {Tr} (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} $ na Equação 1.
$ i (t) = Ke ^ {- \ lgrupo \ frac {t} {\ tau} \ rgrupo} + i_ {ss} (t) $Equation 2
Cálculo da corrente em estado estacionário
Se um sinal senoidal é aplicado como uma entrada para um circuito elétrico Linear, ele produz uma saída de estado estacionário, que também é um sinusoidal signal. Os sinais senoidais de entrada e saída terão a mesma frequência, mas diferentes amplitudes e ângulos de fase.
Podemos calcular a resposta de estado estacionário de um circuito elétrico, quando ele é excitado por uma fonte de tensão senoidal usando Laplace Transform approach.
O diagrama de circuito do domínio s, quando o switch é em closed posição, é mostrado na figura a seguir.
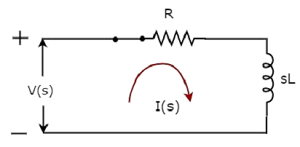
No circuito acima, todas as quantidades e parâmetros são representados em s-domain. Essas são as transformadas de Laplace de parâmetros e quantidades no domínio do tempo.
o Transfer function do circuito acima é
$$ H (s) = \ frac {I (s)} {V (s)} $$
$$ \ Rightarrow H (s) = \ frac {1} {Z (s)} $$
$$ \ Rightarrow H (s) = \ frac {1} {R + sL} $$
Substitua $ s = j \ omega $ na equação acima.
$$ H (j \ omega) = \ frac {1} {R + j \ omega L} $$
Magnitude of $ \ mathbf {\ mathit {H (j \ omega)}} $ é
$$ | H (j \ omega) | = \ frac {1} {\ sqrt {R ^ 2 + {\ omega} ^ 2} L ^ 2} $$
Phase angle of $ \ mathbf {\ mathit {H (j \ omega)}} $ é
$$ \ angle H (j \ omega) = -tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup $$
Vamos pegar o steady state current $ i_ {ss} (t) $ seguindo as duas etapas a seguir -
Multiplique a tensão de pico da tensão sinusoidal de entrada e a magnitude de $ H (j \ omega) $.
Adicione os ângulos de fase da tensão sinusoidal de entrada e $ H (j \ omega) $.
o steady state current $ i_ {ss} (t) $ será
$$ i_ {ss} (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgrupo \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
Substitua o valor de $ i_ {ss} (t) $ na Equação 2.
$ i (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $Equation 3
Sabemos que não há corrente inicial no circuito. Portanto, substitua t = 0 & i (t) = 0 na Equação 3 para encontrar o valor da constante, K.
$$ 0 = Ke ^ {- \ lgrupo \ frac {0} {\ tau} \ rgrupo} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgrupo \ omega (0) + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
$$ \ Rightarrow 0 = K + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgrupo \ varphi - tan ^ {- 1} \ lgrupo \ frac {\ omega L} {R} \ rgroup \ rgroup $$
$$ \ Rightarrow K = - \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgrupo \ varphi - tan ^ {- 1} \ lgrupo \ frac {\ omega L} {R} \ rgroup \ rgroup $$
Substitua o valor de K na Equação 3.
$ i (t) = - \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgrupo \ varphi - tan ^ {- 1} \ lgrupo \ frac {\ omega L} {R} \ rgroup \ rgroup e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2 }} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $Equation 4
A Equação 4 representa a corrente fluindo através do circuito em série RL, quando é excitada por uma fonte de tensão senoidal. É ter dois mandatos. O primeiro e o segundo termos representam a resposta transitória e a resposta de estado estacionário da corrente, respectivamente.
Podemos neglect the first termda Equação 4 porque seu valor será muito menor do que um. Então, a corrente resultante fluindo através do circuito será
$$ i (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgrupo \ omega t + \ varphi - tan ^ {- 1} \ lgrupo \ frac {\ omega L} {R} \ rgroup \ rgroup $$
Contém apenas o steady state term. Portanto, podemos encontrar apenas a resposta de estado estacionário dos circuitos CA e negligenciar a resposta transitória dela.