การให้เหตุผล - เลขฐานสองที่เข้ารหัส
จำนวนที่มีฐาน 2 เรียกว่าเลขฐานสอง เลขฐานสองเกิดจากการเติมเต็ม 0 และ 1 ดังนั้นเลขฐานสองที่เข้ารหัสประกอบด้วยสองกระบวนการ หนึ่งคือการแปลงไบนารีเป็นทศนิยมและอีกรายการหนึ่งคือฐานสิบเป็นฐานสอง
เลขฐานสิบ
อยากรู้อะไร binary numberก่อนอื่นเราต้องรู้เกี่ยวกับเลขฐานสิบ ดังนั้นเลขฐานสิบประกอบด้วยตัวเลขสิบหลัก (เช่น 0,1,2,3,4,5,6,7,8,9) ระบบทศนิยมสามารถแสดงได้โดยใช้ตัวเลขเหล่านี้ ตัวอย่างเช่นลำดับของตัวเลขคือ 2, 4, 6 และ 8 เราทำในลักษณะต่อไปนี้ -
2468 = 2 × 10 3 + 4 × 10 2 + 6 × 10 1 + 8 × 10 0
= 2468
Note- เราได้ค่าของตัวเลขในกรณีนี้โดยการคูณตัวเลขของลำดับต่างๆด้วยกำลัง 10 แล้วบวก 10 นี้เรียกว่าฐานหรือรัศมี ดังนั้นภายใต้ระบบทศนิยมฐานของเราคือ 10
เลขฐานสอง
เราใช้ตัวเลขสิบหลักเพื่อแทนค่า decimal number; เช่นเดียวกับที่เราใช้เพียงสองหลักเพื่อแทนเลขฐานสอง ตัวเลขใด ๆ สามารถแสดงโดยใช้ตัวเลขสองหลักนี้คือ 0 และ 1
ตัวอย่างของเลขฐานสองคือ - 1101 ที่นี่มี 4 หลักในลำดับของตัวเลข - 1, 1, 0, 1 เราได้รับค่าในลักษณะต่อไปนี้
1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0
= 8 + 4 + 0 + 1 = 13
ดังนั้นเลขฐานสองจึงแสดงถึงสิบสามในระบบฐานสิบ ค่าสามารถกำหนดได้โดยmultiplying different digits ของลำดับโดยยกกำลัง 2 และการเพิ่ม
Conventional method - ในตัวอย่างข้างต้นเราจะเห็นว่าในการรับค่าของเลขฐานสองใด ๆ เราใช้กฎต่อไปนี้ -
หลักแรกจากทางขวาคูณด้วย 2 0 = 1
หลักที่สองจากด้านขวาคูณด้วย 2 1 = 2
หลักที่สามจากด้านขวาคูณด้วย 2 2 = 4
ในทำนองเดียวกัน n THหลักจากขวาคูณด้วย 2 n-1
ในที่สุดสิ่งเหล่านี้จะถูกเพิ่มเข้ามา
For Example - แปลงเลขฐานสองต่อไปนี้เป็นเลขฐานสิบ
A - 1010
B - 1111
C - 100
D - 10,000
Solution -
ก - 1010 = 1 × 2 3 + 0 × 2 2 + 1 × 2 1 + 0 × 2 0
B - 1111 = 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0
C - 100 = 1 × 2 2 + 0 × 2 1 + 0 × 2 0
D - 10,000 = 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 0 × 2 0
วิธีที่เร็วกว่า
Step I- เริ่มจากหลักทางขวาของตัวเลขที่กำหนดให้เขียน 1, 2, 4, 8, 16, 32 ……. และด้านล่างแต่ละหลักในขณะที่คุณเดินไปทางซ้าย
Step II- ละเว้นตัวเลขที่ต่ำกว่า 0 วินาที เพิ่มตัวเลขทั้งหมดด้านล่าง 1s
ลองแก้ตัวอย่างที่ 1 โดยวิธีนี้
ก - 1010
เราจะใช้ 1,2,4,8 เพราะนี่คือตัวเลข 4 หลัก
เราได้รับ,
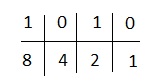
4 และ 1 อยู่ต่ำกว่าศูนย์ เราไม่สนใจพวกเขาและเพิ่มส่วนที่เหลือ เราได้ 8 + 2 = 10
เช่นนี้เราสามารถแก้ตัวเลขอื่นได้
เลขฐานสิบสามารถแปลงเป็นเลขฐานสองโดยวิธีการ successive divisions. แต่ละครั้งของการหารเงินปันผลจะถูกหารด้วย 2 การแจ้งเตือนจะถูกบันทึกไว้และผลหารจะกลายเป็นเงินปันผลครั้งต่อไปซึ่งจะถูกหารด้วย 2 อีกครั้งกระบวนการนี้จะทำซ้ำจนกว่าจะไม่สามารถหารได้อีก
ตัวอย่างเช่น - แปลง 17 เป็นเลขฐานสอง -
หาร 17 ด้วย 2 จนกว่าจะไม่สามารถหารได้อีก
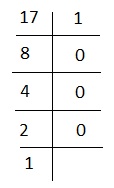
ดังนั้นรูปแบบไบนารีของ 17 คือ 10001
Direction (Q. 1-4) − Study the following question and give the answer.
ในรหัสหนึ่งสัญลักษณ์สำหรับ 0 คือ + และสำหรับ 1 คือ # ไม่มีตัวเลขหรือสัญลักษณ์ใดที่มากกว่า 1 ค่าของสัญลักษณ์สำหรับ 1 จะเพิ่มตัวเองเป็นสองเท่าทุกครั้งที่เลื่อนตำแหน่งหนึ่งไปทางซ้าย
"0" แสดงเป็น +
'1' แสดงเป็น #
'2' แสดงเป็น # +
'3' แสดงเป็น ##
'4' แสดงเป็น # ++ และอื่น ๆ
1 - ข้อใดต่อไปนี้จะแสดงถึง 11?
Options -
A - # + ##
B - + ## +
C - ## ++
D - # + # ++
E - ไม่มีสิ่งเหล่านี้
Answer - ตัวเลือกก
Explanation - เพื่อให้ได้เท่ากับ 11 เราใช้วิธีการหารต่อเนื่องด้วย 2

ดังนั้นรูปแบบไบนารีจะเป็น 10111 แทนที่ 1 และ 0 ด้วย # และ + เราจะได้ # + ##
2 - ข้อใดจะแสดงถึง 8?
Options -
A - ## ++
B - + ## +
C - ## ++
D - ++ ##
E - ไม่มีสิ่งเหล่านี้
Answer - ตัวเลือก E
Explanation - สำหรับ 8 เรามี -
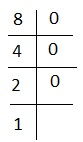
เช่น 1,000 หรือ # +++ ตัวเลือกที่ถูกต้องคือ 5
3 - ข้อใดต่อไปนี้จะแสดงโดย ## + #?
Options -
A - 8
B - 11
C - 13
D - 12
E - ไม่มีสิ่งเหล่านี้
Answer - ตัวเลือก E
Explanation- ## + # = 1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 = 15
4 - หมายเลขใดต่อไปนี้จะแสดงด้วย # +++ #?
Options -
A - 22
B - 31
C - 14
D - 17
E - ไม่มีสิ่งเหล่านี้
Answer - ตัวเลือก D
Explanation - # + + + # = 10001
= 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0
= 16 + 1 = 17
ระบบเลขฐานสองมีฐาน 2 ระบบฐานสิบมีฐาน 10 และระบบตติยภูมิมีฐาน 3 ในขณะที่ระบบฐานแปดมีฐาน 8 ในกรณีของตติยภูมิเรามีสามหลักแทนตัวเลข เหล่านี้คือ 0, 1 และ 2 ในกรณีนี้ตัวเลขจะถูกแปลงเป็นทศนิยมโดยการคูณด้วยเลข 3 ที่เหมาะสม
For Example -
(12012) 3 = 1 × 3 4 + 2 × 3 3 + 0 × 3 2 + 1 × 3 1 + 2 × 3 0 = (104) 3