การใช้เหตุผล - แผนภาพเวนน์ตรรกะ
เป็นกระบวนการแสดงความสัมพันธ์ที่ซับซ้อนระหว่าง 2-3 หมวดหมู่ตามแผนภาพผ่านการเข้มงวดทางเรขาคณิตต่างๆ จุดตัดระหว่างโครงสร้างทางเรขาคณิตสองโครงสร้างบ่งชี้ว่าพวกมันมีบางอย่างที่เหมือนกันและการแยกทั้งหมดบ่งชี้ว่าตรงกันข้าม แม้ว่าทฤษฎีจะดูซับซ้อนจากข้างต้น แต่ความเข้าใจพื้นฐานเกี่ยวกับกรณีตัวอย่างประเภทต่างๆจะช่วยในการแก้คำถามที่ตามมาได้ง่ายขึ้น
ดูกรณีที่เป็นไปได้ต่างๆของแผนภาพเวนน์และทราบว่าเมื่อใดที่สามารถใช้ได้ ในสามคอลัมน์คอลัมน์แรกแสดงประเภทของแผนภาพเวนน์คอลัมน์ที่สองใช้สำหรับคำอธิบายและไซต์ที่สามเป็นตัวอย่างเพื่อให้เห็นภาพที่ชัดเจนของคำอธิบาย
| แผนภาพเวนน์ | กรณีที่เกี่ยวข้อง | ตัวอย่าง |
|---|---|---|
|
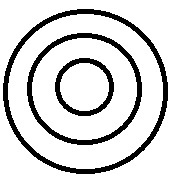
จะมีชุดย่อยของเคสย่อยอีกชุดหนึ่ง |
สี> เขียว> เขียวอ่อน สีเขียวอ่อนเป็นส่วนย่อยของสีเขียวและทั้งคู่อยู่ในกลุ่มสี |
|
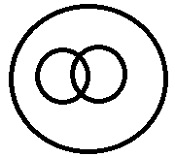
หมวดหมู่หลักหมวดหมู่หนึ่งภายใต้หมวดหมู่ย่อยสองหมวดหมู่และทั้งสองมีความคล้ายคลึงกัน |
ของเหลว> เบนซินดีเซล ทั้งสองอย่างนี้มีลักษณะเป็นวัตถุไวไฟดังนั้นจึงมีความคล้ายคลึงกัน |

|
หมวดหมู่หนึ่งอาจมีหมวดหมู่ย่อยหนึ่งหมวด ทั้งคู่ปฏิบัติตามเงื่อนไขบางส่วน (ไม่เสมอไป) |
ผัก> พริก> แดง พริกบางชนิดมีสีแดงและเช่นเดียวกับผักอื่น ๆ |
|
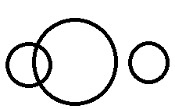
ในสามส่วนที่แตกต่างกันสองส่วนอาจมีคุณสมบัติทั่วไปบางอย่างที่ไม่ตรงกับส่วนที่สาม |
นักแสดง> อาจารย์ใหญ่> ราชินี. จากที่กล่าวมานักแสดงและอาจารย์ใหญ่แสดงความเป็นชายดังนั้นจึงมีคุณสมบัติทั่วไปบางประการซึ่งตรงข้ามกับราชินี |
|
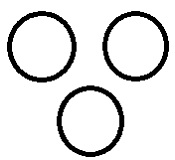
สามส่วนที่ไม่มีคุณสมบัติทั่วไป |
ต้นไม้> โกรธ> กาแฟ ไม่มีตรรกะในการค้นหาแง่มุมทั่วไปในสามคำข้างต้น |

|
มีโอกาสที่จะพบสถานที่ทั่วไปที่ตรงตามคุณสมบัติทั้งหมดของสามส่วนแต่ละส่วน |
แม่> แม่เลี้ยง> พี่สะใภ้. ผู้หญิงคนเดียวสามารถเป็นทั้งหมดที่กล่าวมาพร้อมกัน |

|
โดยเฉพาะอย่างยิ่งสำหรับกรณีเหล่านั้นซึ่งในสามส่วนสองส่วนเกี่ยวข้องกันในฐานะความสัมพันธ์ของผู้ปกครองลูกในขณะที่ส่วนที่สามไม่มีความสัมพันธ์กับพวกเขา |
ต้นไม้> ต้นกล้วย> โกรธ เราทุกคนรู้ว่าต้นกล้วยอยู่ในหมวดต้นไม้ แต่อารมณ์ "โกรธ" ไม่มีส่วนเกี่ยวข้องกับ 2 คำนี้ |
คำถามอีกประเภทหนึ่งที่มักเกิดขึ้นภายใต้บทนี้คือการตัดกันของโครงสร้างทางเรขาคณิตต่างๆ โครงสร้างทางเรขาคณิตแต่ละแบบจะมีองค์ประกอบบางอย่างเป็นของตัวเองและแต่ละโครงสร้างจะมีลักษณะหรือคลาสบางอย่าง การตัดกันของโครงสร้างตั้งแต่สองโครงสร้างขึ้นไปจะทำให้เกิดการผสมผสานที่จะเปลี่ยนคุณสมบัติของแต่ละองค์ประกอบก่อนหน้าด้วยสิ่งใหม่ เราต้องระบุสิ่งนั้นและจำเป็นต้องตอบตามตัวเลือกที่กำหนด
ห้าคนเป็นหมายเลขและมีลักษณะบางอย่าง ศึกษาแผนภาพเพื่อตอบถูก

1 - คนเลขไหนฉลาดและน่ารัก?
A - 1
B - 2
C - 3
D - 4
Answer - ตัวเลือก B
Explanation - หมายเลข 2 อยู่ในพื้นที่ส่วนกลางของสี่เหลี่ยมจัตุรัสและวงกลมดังนั้นจึงมีลักษณะของโครงสร้างทั้งสอง
2 - คนหมายเลขไหนฉลาด แต่ไม่สุภาพและน่ารัก?
A - 1
B - 2
C - 3
D - 4
Answer - ตัวเลือก D
Explanation - หมายเลข 4 อยู่ในพื้นที่วงกลมจึงมีลักษณะเฉพาะของความฉลาด
3 - คนเลขไหนฉลาดสุภาพและน่ารัก?
A - 1
B - 2
C - 3
D - ไม่มีทั้งหมดข้างต้น
Answer - ตัวเลือก D
Explanation - ไม่มีตัวเลขดังกล่าวอยู่ในพื้นที่จุดตัดของโครงสร้างทางเรขาคณิตทั้งสาม