Maliyet Muhasebesi - CVP Analizi

Maliyet-Hacim-Kar (CVP) Analizi, Başabaş Noktası Analizi olarak da bilinir. Her işletme organizasyonu karını maksimize etmek için çalışır. Yönetim, CVP analizi yardımıyla kar ve üretim seviyesi arasındaki ilişkiyi inceler.

CVP analizi, toplam satışın toplam maliyete eşit olduğu faaliyet seviyesiyle ilgilidir ve başa baş noktası olarak adlandırılır. Başka bir deyişle, satış değerini, maliyeti ve karı farklı üretim seviyelerinde inceliyoruz. CVP analizi, maliyet, satış değeri ve kâr arasındaki ilişkiyi vurgular.

Varsayımlar

CVP analizi için varsayımları gözden geçirelim:

Değişken maliyetler değişken ve sabit maliyetler her üretim düzeyinde sabit kalır.
Satış hacmi, ürünün satış fiyatını etkilemez. Satış fiyatının sabit olduğunu varsayabiliriz.
Tüm satış seviyelerinde hacim, malzeme ve işçilik maliyetleri sabit kalır.
Verimlilik ve üretkenlik, satış hacminin tüm seviyelerinde değişmeden kalır.
Tüm satış seviyelerindeki satış karması, çok ürünlü bir durumda sabit kalır.
Maliyet ve geliri etkileyen ilgili faktör yalnızca hacimdir.
Satış hacmi, üretim hacmine eşittir.

Marjinal Maliyet Denklemi

Maliyet unsurları için denklemler aşağıdaki gibidir:

Sales = Variable costs + Fixed Expenses ± Profit /Loss

                     Or
                     
Sales – Variable Cost = Fixed Expenses ± Profit /Loss

                     Or
                     
Sales – Variable Cost = Contribution

Maliyet, hacim ve kâr arasındaki matematiksel ilişkiyi bilmek için aşağıdaki dört kavramı, hesaplamalarını ve uygulamalarını anlamak gerekir:

Contribution
Kar Hacim Oranı (P / V Oranı veya Katkı / Satışlar (C / S))
Başa Baş Noktası
Güvenlik marjı

Katkı

Contribution = Sales – Marginal Cost

Yukarıdaki Marjinal Maliyet konusuna katkıyı zaten tartışmıştık.

Kar-Hacim Oranı

Kar / Hacim (P / V) oranı, bir işletmenin faaliyetlerinin karlılığını incelerken ve Satış ve Katkı arasında bir ilişki kurmak için hesaplanır. Aşağıdaki gibi hesaplanan en önemli oranlardan biridir:

^P ⁄ _V Oranı =

Katkı / Satış

Sabit Giderler + Kar / Satış

Satışlar − Değişken Maliyet / Satışlar

Katkı Karındaki Değişim / Satışlardaki Değişim

F / V Oranı, karla doğrudan bir ilişki paylaşır. P / V oranı ne kadar yüksekse, o kadar çok kâr ve tam tersi.

Başa Baş Noktası

Bir işi yürütmenin toplam maliyeti toplam satışa eşit olduğunda, buna başabaş noktası denir. Katkı bu noktada sabit maliyete eşittir. İşte başabaş noktasını hesaplamak için bir formül:

BEP (birim cinsinden) =

Toplam Sabit Giderler / Birim Başına Satış Fiyatı - Birim Başına Marjinal Maliyet

Birim Başına Toplam Sabit Gider / Katkı

Toplam satışa göre başa baş noktası:

Sabit Maliyet / ^P ⁄ _V Oranı

İstenilen bir karın kazanıldığı çıktı veya satış değerinin hesaplanması:

Sabit Giderler + Birim Başına İstenilen Kar / Satış Fiyatı - Birim Başına Marjinal Maliyet

Sabit Giderler + Birim Başına İstenilen Kar / Katkı

Bileşik Kırılma Noktası

Bir şirketin aynı ürünü üretebilecekleri farklı üretim birimleri olabilir. Bu durumda, BEP'i bulmak için her bir üretim biriminin birleşik sabit maliyeti ve birleşik toplam satışlar dikkate alınır.

Constant Product - Karışım Yaklaşımı Bu yaklaşımda, tüm üretim birimlerinin ürünleri için oran sabittir.
Variable Product - Karışım Yaklaşımı Bu yaklaşımda ürünlerin tercihi daha büyük orana dayanmaktadır.

Güvenlik marjı

BEP'de satış fazlası, güvenlik payı olarak bilinir. Bu nedenle,

Margin of safety = Actual Sales − Sales at BEP

Aşağıdaki formül yardımıyla güvenlik marjı hesaplanabilir:

Güvenlik Marjı =

Kar / ^P ⁄ _V Oranı

Birim Kâr / Katkı

Başabaş Grafiği

Başabaş Çizelgesi, marjinal maliyetlemenin en kullanışlı grafik gösterimidir. Muhasebe verilerini kullanışlı bir okunabilir rapora dönüştürür. Tahmini karlar, zararlar ve maliyetler farklı üretim seviyelerinde belirlenebilir. Bir örnek ele alalım.

Misal

Kesinti noktasını hesaplayın ve aşağıdaki verilerden başa baş grafiğini çizin:

Fixed Cost    = Rs 2,50,000
Variable Cost = Rs 15 per unit
Selling Price = Rs 25 per unit
Production level in units 12,000, 15,000, 20,000, 25,000, 30,000, and 40,000.

Solution:

BEP =

Birim başına Sabit Maliyet / Katkı

2,50,000 Rupi / 10 Rs (25 Rs - 15 Rs)

= 25.000 birim

25.000 adet üretim seviyesinde, toplam maliyet 6,25,000 Rs olacaktır.

((25000 × 14) + 2.50000 olarak hesaplanmıştır)

Farklı üretim seviyelerinde Kar ve Güvenlik Marjını gösteren Beyan Eşit Satış Satışı = 6,25,000 Rs (25,000 x 25)
Üretim (Birimlerde)	Toplam satış (Rs cinsinden)	Toplam tutar (Rs cinsinden)	Kar (Satış - Maliyet) (Rs cinsinden)	Güvenlik marjı (Birim başına Kâr / Katkı) (Birimlerde)
12000	3.00.000	4.30.000	-1.30.000
15.000	3.75.000	4.75.000	-1,00,000
20.000	5,00,000	5,50,000	-50.000
25.000	6,25,000	6,25,000	(BEP)	(BEP)
30000	7,50,000	7,00,000	50.000	5.000
40000	10,00,000	8,50,000	1.50.000	15.000

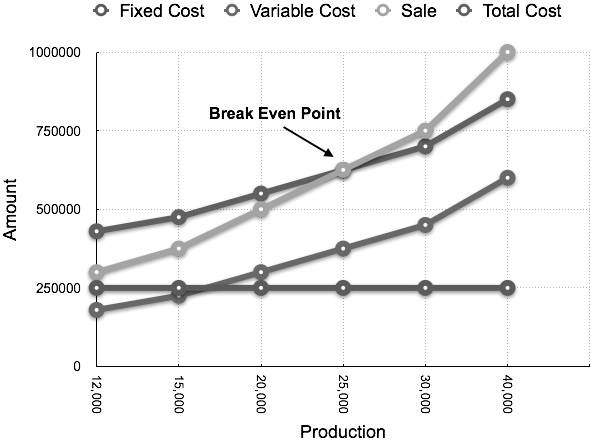
Miktar bazında üretim olarak çizilen ilgili grafik aşağıdaki gibi görünür: