Ayrık Matematik - Grup Teorisi

Yarıgrup

$ '\ Omicron' $ (Bileşim) ikili işlemine sahip sonlu veya sonsuz bir $ 'S' $ kümesi, iki koşulu aynı anda tutuyorsa yarı grup olarak adlandırılır -

Closure - S'deki her $ (a, b) \ çifti için, \ :( a \ omicron b) $ $ S $ kümesinde bulunmalıdır.
Associative - S'deki her $ a, b, c \ öğesi için, (a \ omicron b) \ omicron c = a \ omicron (b \ omicron c) $ tutmalıdır.

Misal

Toplama işlemi ile pozitif tamsayılar kümesi (sıfır hariç) bir yarı gruptur. Örneğin, $ S = \ lbrace 1, 2, 3, \ dots \ rbrace $

Burada, S'deki her $ (a, b) \ çiftinde olduğu gibi kapatma özelliği tutulur, (a + b) $ S kümesinde bulunur. Örneğin, $ 1 + 2 = 3 \ S] $

İlişkili özellik ayrıca S, (a + b) + c = a + (b + c) $ içindeki her $ a, b, c \ öğesi için de geçerlidir. Örneğin, $ (1 + 2) + 3 = 1 + (2 + 3) = 5 $

Monoid

Monoid, kimlik öğesi olan bir yarı gruptur. Bir S kümesinin kimlik öğesi ($ e $ veya E ile gösterilir), S $ içindeki her $ a \ öğesi için $ (a \ omicron e) = a $ olacak şekilde bir öğedir. Bir kimlik unsuru aynı zamandaunit element. Yani, bir monoid aynı anda üç özelliğe sahiptir -Closure, Associative, Identity element.

Misal

Çarpma işlemi ile pozitif tamsayılar kümesi (sıfır hariç) bir monoiddir. $ S = \ lbrace 1, 2, 3, \ dots \ rbrace $

Burada, S'deki her $ (a, b) \ çifti için, (a \ times b) $, S kümesinde olduğu gibi kapatma özelliği tutar. [Örneğin, S $ içinde $ 1 \ times 2 = 2 \ ve benzeri]

İlişkili özellik ayrıca S içindeki her $ a, b, c \ öğesi için de tutar, (a \ times b) \ times c = a \ times (b \ times c) $ [Örneğin, $ (1 \ times 2) \ times 3 = 1 \ times (2 \ times 3) = 6 $ ve benzeri]

Kimlik özelliği, S içindeki her $ a \ öğesi için de tutar, (a \ times e) = a $ [Örneğin, $ (2 \ times 1) = 2, (3 \ times 1) = 3 $ vb.]. Burada kimlik öğesi 1'dir.

Grup

Bir grup, ters elemanlı bir monoiddir. Bir S kümesinin ters elemanı (I ile gösterilir), S $ 'daki her bir $ a \ elemanı için $ (a \ omicron I) = (I \ omicron a) = a $ olacak şekilde bir elemandır. Bu nedenle, bir grup aynı anda dört özelliğe sahiptir - i) Kapanış, ii) İlişkisel, iii) Kimlik öğesi, iv) Ters öğe. Bir G grubunun sırası, G'deki elemanların sayısıdır ve bir gruptaki bir elemanın sırası, en az pozitif tamsayıdır n, öyle ki an, bu G grubunun kimlik elemanıdır.

Örnekler

$ N \ times N $ tekil olmayan matrisler kümesi, matris çarpım işlemi altında bir grup oluşturur.

İki $ N \ times N $ tekil olmayan matrisin çarpımı da kapanış özelliğini tutan $ N \ times N $ tekil olmayan bir matristir.

Matris çarpımının kendisi ilişkiseldir. Bu nedenle, birleştirici mülkiyet hakları vardır.

$ N \ times N $ tekil olmayan matrisler kümesi, kimlik öğesi özelliğini tutan kimlik matrisini içerir.

Tüm matrisler tekil olmadıklarından, hepsinin aynı zamanda tekil olmayan matrisler olan ters elemanları vardır. Dolayısıyla, ters mülkiyet de geçerlidir.

Abelian Grubu

Bir değişmeli grup G, G $ 'daki $ (a, b) \ eleman çiftinin her zaman değişme yasasına sahip olduğu bir gruptur. Dolayısıyla, bir grup aynı anda beş özelliğe sahiptir - i) Kapanış, ii) İlişkisel, iii) Kimlik öğesi, iv) Ters öğe, v) Değişmeli.

Misal

Toplama işlemi ile pozitif tamsayılar kümesi (sıfır dahil) değişmeli bir gruptur. $ G = \ lbrace 0, 1, 2, 3, \ dots \ rbrace $

Burada, S'deki her $ (a, b) \ çiftinde olduğu gibi kapanma özelliği geçerli olur, (a + b) $ S kümesinde bulunur [Örneğin, S $ içinde $ 1 + 2 = 2 \ vb.]

İlişkili özellik ayrıca S'deki her $ a, b, c \ öğesi için de geçerlidir, (a + b) + c = a + (b + c) $ [Örneğin, $ (1 +2) + 3 = 1 + (2 + 3) = 6 $ ve benzeri]

Kimlik özelliği, S içindeki her $ a \ öğesi için de tutar, (a \ times e) = a $ [Örneğin, $ (2 \ times 1) = 2, (3 \ times 1) = 3 $ vb.]. Burada kimlik öğesi 1'dir.

Değişmeli özellik ayrıca S'deki her $ a \ öğesi için de tutar, (a \ times b) = (b \ times a) $ [Örneğin, $ (2 \ times 3) = (3 \ times 2) = 3 $ ve benzeri üzerinde]

Döngüsel Grup ve Alt Grup

Bir cyclic grouptek bir eleman tarafından oluşturulabilen bir gruptur. Döngüsel bir grubun her elemanı, bir jeneratör adı verilen belirli bir elemanın gücüdür. Döngüsel bir grup, bir jeneratör 'g' tarafından oluşturulabilir, öyle ki grubun diğer her elemanı jeneratör 'g' gücü olarak yazılabilir.

Misal

Çarpma işlemi altındaki $ \ lbrace 1, -1, i, -i \ rbrace $ karmaşık sayılar kümesi döngüsel bir gruptur.

İki üretici vardır - $ i $ ve $ –i $ as $ i ^ 1 = i, i ^ 2 = -1, i ^ 3 = -i, i ^ 4 = 1 $ ve ayrıca $ (- i) ^ 1 = -i, (–i) ^ 2 = -1, (–i) ^ 3 = i, (–i) ^ 4 = 1 $ grubun tüm elemanlarını kapsar. Dolayısıyla, döngüsel bir gruptur.

Note - bir cyclic groupher zaman değişmeli bir gruptur, ancak her değişmeli grup bir döngüsel grup değildir. Toplanan rasyonel sayılar döngüsel değildir, değişkendir.

Bir subgroup H, dört özelliği aynı anda karşılarsa, G grubunun bir alt kümesidir ($ H ≤ G $ ile gösterilir) - Closure, Associative, Identity element, ve Inverse.

G grubunun tamamını içermeyen bir G grubunun bir H alt grubuna uygun bir alt grup denir ($ H <G $ ile gösterilir). Bir siklik grubun bir alt grubu döngüseldir ve bir değişmeli alt grup da değişmeli.

Misal

Bir $ G = \ lbrace 1, i, -1, -i \ rbrace $ grubu olsun

O zaman bazı alt gruplar $ H_1 = \ lbrace 1 \ rbrace, H_2 = \ lbrace 1, -1 \ rbrace $,

Bu bir alt grup değil - $ H_3 = \ lbrace 1, i \ rbrace $ çünkü bu $ (i) ^ {- 1} = -i $ $ H_3 $ içinde değil

Kısmen Sipariş Edilmiş Set (POSET)

Kısmen sıralı bir küme, dönüşlü, antisimetrik ve geçişli bir ikili ilişkiye sahip bir kümeden oluşur. "Kısmen sıralı küme" POSET olarak kısaltılır.

Örnekler

İkili işlem altında $ (\ le) $ 'dan küçük veya ona eşit gerçek sayılar kümesi bir posettir.

$ S = \ lbrace 1, 2, 3 \ rbrace $ küme ve işlem $ \ le $ olsun

İlişkiler $ \ lbrace (1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3) \ rbrace $ olacaktır

Bu R ilişkisi, R $ 'da $ \ lbrace (1, 1), (2, 2), (3, 3) \ rbrace \ olarak refleksiftir

Bu R ilişkisi anti-simetriktir.

$ \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace \ in R \ ve \ \ lbrace (1, 2), (1, 3), (2, 3) \ rbrace ∉ R $

Bu R ilişkisi aynı zamanda R $ 'da $ \ lbrace (1,2), (2,3), (1,3) \ rbrace \ gibi geçişlidir.

Bu nedenle, bu bir poset.
'Ulaşılabilirlik' operasyonu altındaki yönlendirilmiş çevrimsiz grafiğin tepe noktası kümesi bir pozettir.

Hasse Diyagramı

Bir kümenin Hasse diyagramı, köşeleri o kümenin öğesi olan ve yaylar kümedeki çiftleri (x, y) kapsayan yönlendirilmiş grafiktir. $ X <y $ kümesinde ise, x noktası Hasse diyagramında y noktasından daha düşük görünür. Eğer konum kümesinde $ x <y <z $ ise, ok örtük olduğu için x ve z arasında gösterilmez.

Misal

$ \ Lbrace 1, 2, 3 \ rbrace = \ lbrace \ emptyset, \ lbrace 1 \ rbrace, \ lbrace 2 \ rbrace, \ lbrace 3 \ rbrace, \ lbrace 1, 2 \ rbrace, \ lbrace 1 alt kümelerinin kümesi , 3 \ rbrace, \ lbrace 2, 3 \ rbrace, \ lbrace 1, 2, 3 \ rbrace \ rbrace $ aşağıdaki Hasse diyagramında gösterilmektedir -

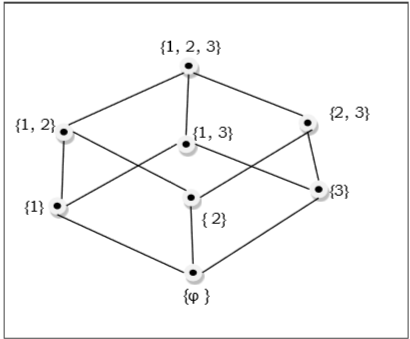
Doğrusal Sıralı Set

Doğrusal sıralı küme veya Toplam sıralı küme, her öğe çiftinin karşılaştırılabilir olduğu kısmi bir sıra kümesidir. $ A \ le b $ veya $ b \ le a $ tutarsa, S $ içindeki $ a, b \ öğelerinin karşılaştırılabilir olduğu söylenir. Trikotomi yasası, bu toplam sıralı seti tanımlar. Tamamen sıralı bir küme, S kümesindeki tüm a ve b değerleri için $ \ lbrace a \ lor b, a \ land b \ rbrace = \ lbrace a, b \ rbrace $ özelliğine sahip bir dağıtıcı kafes olarak tanımlanabilir.

Misal

\ Subseteq tarafından sıralanan $ \ lbrace a, b \ rbrace $ 'ın güç kümesi, $ P = \ lbrace \ emptyset, \ lbrace a \ rbrace, \ lbrace b \ rbrace, \ güç kümesinin tüm öğeleri olarak tamamen sıralı bir kümedir. lbrace a, b \ rbrace \ rbrace $ benzerdir.

Toplam olmayan sipariş seti örneği

X böler y işlemi altında bir $ S = \ lbrace 1, 2, 3, 4, 5, 6 \ rbrace $ kümesi toplam sıralı bir küme değildir.

Burada, S, x | içindeki tüm $ (x, y) \ için y $ tutmalı ama 2 | 3, çünkü 2, 3'ü bölmez veya 3, 2'yi bölmez. Dolayısıyla, toplam sıralı bir küme değildir.

Kafes

Bir kafes, L $ 'daki her $ \ lbrace a, b \ rbrace \ çiftinin en az üst sınıra ($ a \ lor b $ ile gösterilir) ve en büyük alt sınıra sahip olduğu bir $ (L, \ le) $ posetidir. $ a \ land b $ ile gösterilir). LUB $ (\ lbrace a, b \ rbrace) $, a ve b'nin birleşimi olarak adlandırılır. GLB $ (\ lbrace a, b \ rbrace) $, a ve b'nin buluşması olarak adlandırılır.

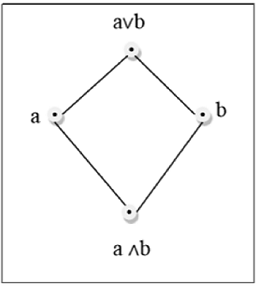
Misal

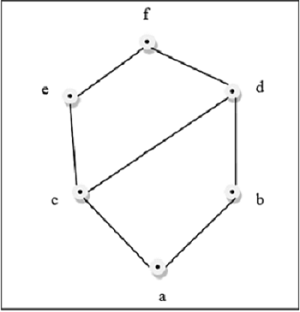
Yukarıdaki şekil bir kafestir çünkü L $ içindeki her $ \ lbrace a, b \ rbrace \ çifti için bir GLB ve bir LUB vardır.

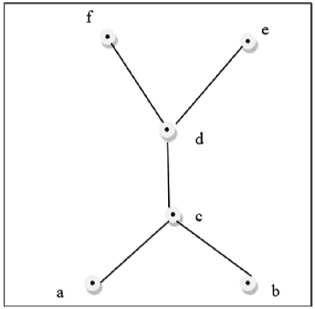
Yukarıdaki şekil bir kafes değildir çünkü $ GLB (a, b) $ ve $ LUB (e, f) $ yoktur.

Diğer bazı kafesler aşağıda tartışılmıştır -

Sınırlı Kafes

Bir L kafes, en büyük 1 ve en az 0 öğelerine sahipse sınırlı bir kafes haline gelir.

Tamamlanmış Kafes

Bir kafes L, sınırlı bir kafes ise ve kafesteki her elemanın bir tamamlayıcısı varsa, tamamlanmış bir kafes haline gelir. Bir x elemanının tamamlayıcısı x 'e sahiptir eğer $ \ varsa x (x \ land x' = 0 ve x \ lor x '= 1) $