Ayrık Matematik - Ağaçları Kapsayan
Bağlı bir yönsüz grafiğin ($ G $) yayılan ağacı, $ G $ 'ın tüm köşelerini minimum düzeyde içeren bir ağaçtır. Bir grafiğin birçok yayılan ağacı olabilir.
Misal
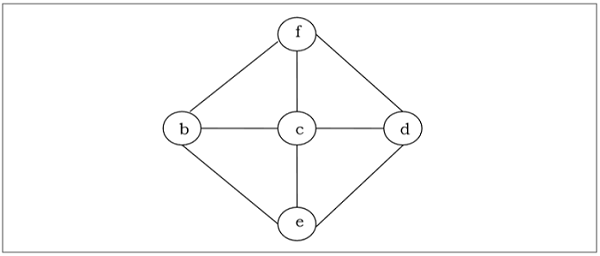
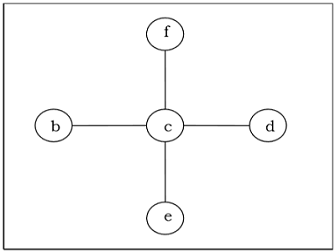
Az yer kaplayan ağaç
Ağırlıklı, bağlantılı ve yönlendirilmemiş bir grafiğin ($ G $) olası her kapsama ağacının ağırlığından daha az veya buna eşit ağırlık atanmış bir kapsayan ağaç, buna minimum kapsayan ağaç (MST) denir. Kapsayan bir ağacın ağırlığı, kapsayan ağacın her bir kenarına atanan tüm ağırlıkların toplamıdır.
Misal
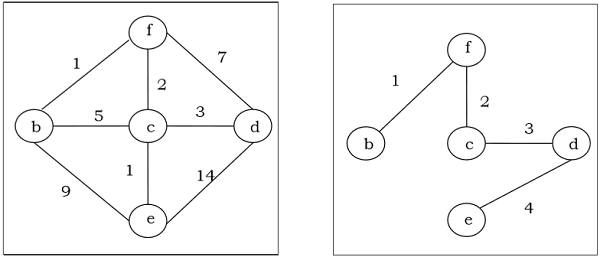
Kruskal Algoritması
Kruskal'ın algoritması, bağlantılı bir ağırlıklı grafik için minimum bir yayılma ağacı bulan açgözlü bir algoritmadır. Bu grafiğin her tepe noktasını içeren bir ağacı bulur ve ağaçtaki tüm kenarların toplam ağırlığı, olası her yayılma ağacından daha az veya ona eşittir.
Algoritma
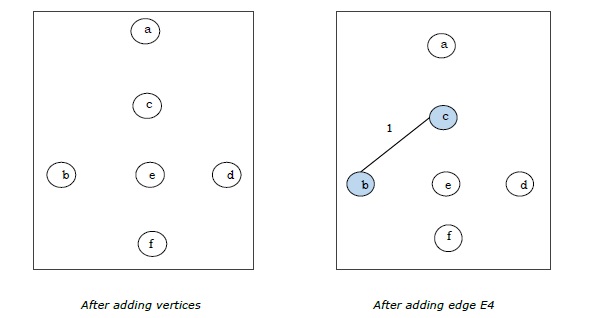
Step 1 - Verilen grafiğin tüm kenarlarını $ G (V, E) $ kenar ağırlıklarına göre artan sırada düzenleyin.
Step 2 - Grafikten en küçük ağırlıklı kenarı seçin ve şimdiye kadar oluşturulan kapsayan ağaçla bir döngü oluşturup oluşturmadığını kontrol edin.
Step 3 - Döngü yoksa, bu kenarı kapsayan ağaca dahil edin, yoksa atın.
Step 4 - Kapsayan ağaçta $ (V-1) $ sayıda kenar kalana kadar Adım 2 ve Adım 3'ü tekrarlayın.
Problem
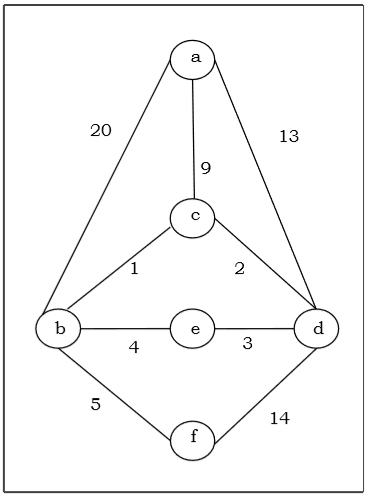
Kruskal algoritmasını kullanarak aşağıdaki G grafiği için minimum yayılma ağacını bulmak istediğimizi varsayalım.
Solution
Yukarıdaki grafikten aşağıdaki tabloyu oluşturuyoruz -
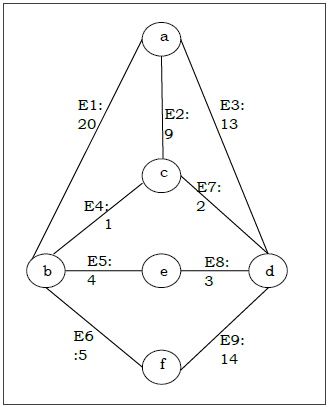
| Kenar No. | Köşe Çifti | Kenar Ağırlığı |
|---|---|---|
| E1 | (a, b) | 20 |
| E2 | (AC) | 9 |
| E3 | (a, d) | 13 |
| E 4 | (M.Ö) | 1 |
| E5 | (b, e) | 4 |
| E6 | (b, f) | 5 |
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E9 | (d, f) | 14 |
Şimdi tabloyu Kenar ağırlığına göre artan sırada yeniden düzenleyeceğiz -
| Kenar No. | Köşe Çifti | Kenar Ağırlığı |
|---|---|---|
| E 4 | (M.Ö) | 1 |
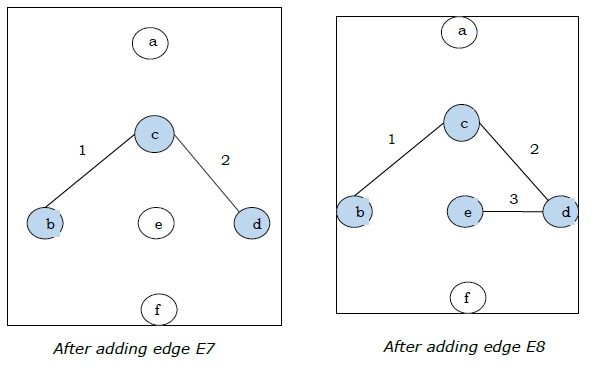
| E7 | (c, d) | 2 |
| E8 | (d, e) | 3 |
| E5 | (b, e) | 4 |
| E6 | (b, f) | 5 |
| E2 | (AC) | 9 |
| E3 | (a, d) | 13 |
| E9 | (d, f) | 14 |
| E1 | (a, b) | 20 |
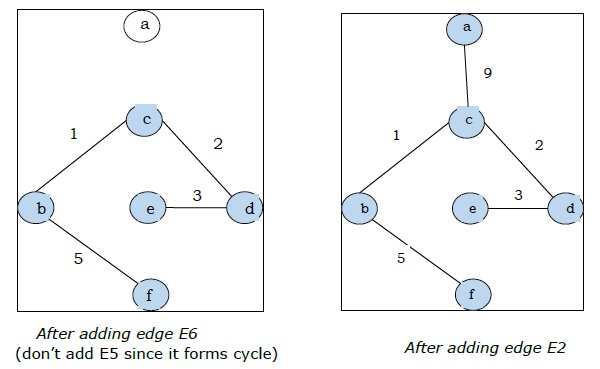
Son şekildeki 5 kenarın hepsini aldığımız için algoritmayı durdururuz ve bu minimum uzanan ağaç ve toplam ağırlığı $ (1 + 2 + 3 + 5 + 9) = 20 $.
Prim Algoritması
Prim'in matematikçiler, Vojtech Jarnik ve Robert C. Prim tarafından 1930'da keşfedilen algoritması, bağlantılı bir ağırlıklı grafik için minimum bir yayılma ağacı bulan açgözlü bir algoritmadır. Bu grafiğin her tepe noktasını içeren bir ağacı bulur ve ağaçtaki tüm kenarların toplam ağırlığı, olası her yayılma ağacından daha az veya ona eşittir. Prim'in algoritması yoğun grafiklerde daha hızlıdır.
Algoritma
Grafikten rastgele seçilen tek bir tepe noktasıyla minimal yayılma ağacını başlatın.
Tüm köşeler ağaca eklenene kadar 3. ve 4. adımları tekrarlayın.
Ağacı henüz ağaçta olmayan bir tepe noktasına bağlayan bir kenar seçin, böylece kenarın ağırlığı minimum olur ve kenarın dahil edilmesi bir döngü oluşturmaz.
Ağaca bağlandığı seçili kenarı ve tepe noktasını ekleyin.
Problem
Prim algoritmasını kullanarak aşağıdaki G grafiği için minimum yayılma ağacını bulmak istediğimizi varsayalım.
Solution
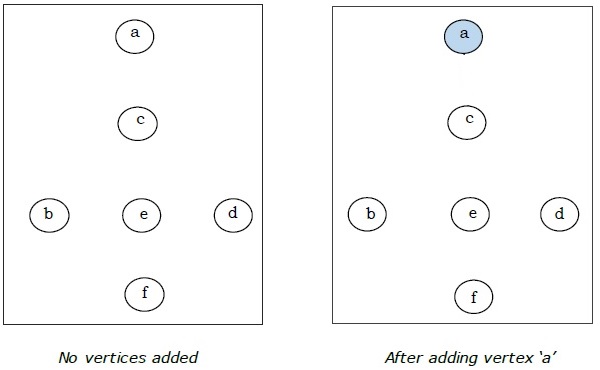
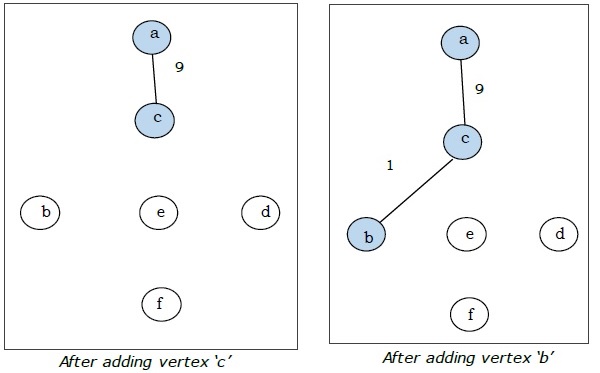
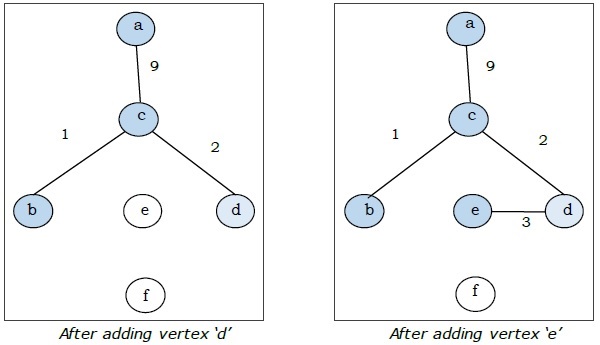
Burada 'a' tepe noktasıyla başlayıp ilerliyoruz.
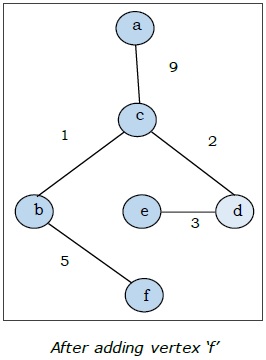
Bu minimum uzanan ağaçtır ve toplam ağırlığı $ (1 + 2 + 3 + 5 + 9) = 20 $ 'dır.