Boolean İşlevlerinin Basitleştirilmesi
Cebirsel Fonksiyonları Kullanarak Basitleştirme
Bu yaklaşımda, Boolean kimlikleri uygulanarak bir Boole ifadesi, eşdeğer bir ifadeye küçültülür.
Problem 1
Boole kimliklerini kullanarak aşağıdaki Boole ifadesini simge durumuna küçültün -
$$ F (A, B, C) = A'B + BC '+ BC + AB'C' $$
Çözüm
Göz önüne alındığında, $ F (A, B, C) = A'B + BC '+ B + AB'C' $
Veya $ F (A, B, C) = A'B + (BC '+ BC') + BC + AB'C '$
[İdempotent yasasına göre, BC '= BC' + BC ']
Veya $ F (A, B, C) = A'B + (BC '+ BC) + (BC' + AB'C ') $
Veya $ F (A, B, C) = A'B + B (C '+ C) + C' (B + AB ') $
[Dağıtım yasalarına göre]
Veya $ F (A, B, C) = A'B + B.1 + C '(B + A) $
[(C '+ C) = 1 ve soğurma kuralı (B + AB') = (B + A)]
Veya $ F (A, B, C) = A'B + B + C '(B + A) $
[B.1 = B]
Veya $ F (A, B, C) = B (A '+ 1) + C' (B + A) $
Veya $ F (A, B, C) = B.1 + C '(B + A) $
[(A '+ 1) = 1]
Veya $ F (A, B, C) = B + C '(B + A) $
[As, B.1 = B]
Veya $ F (A, B, C) = B + BC '+ AC' $
Veya $ F (A, B, C) = B (1 + C ') + AC' $
Veya $ F (A, B, C) = B.1 + AC '$
[As, (1 + C ') = 1]
Veya $ F (A, B, C) = B + AC '$
[As, B.1 = B]
Dolayısıyla, $ F (A, B, C) = B + AC '$ küçültülmüş formdur.
Problem 2
Boole kimliklerini kullanarak aşağıdaki Boole ifadesini simge durumuna küçültün -
$$ F (A, B, C) = (A + B) (A + C) $$
Çözüm
Verildiğinde, $ F (A, B, C) = (A + B) (A + C) $
Veya $ F (A, B, C) = AA + AC + BA + BC $ [Dağıtım Kuralı uygulanıyor]
Veya $ F (A, B, C) = A + AC + BA + BC $ [Belirsizlik Yasasının Uygulanması]
Veya $ F (A, B, C) = A (1 + C) + BA + BC $ [Dağıtım Yasasını Uygulama]
Veya $ F (A, B, C) = A + BA + BC $ [Hakimiyet Yasasını Uygulama]
Veya $ F (A, B, C) = (A + 1) .A + BC $ [Dağıtım Yasasının Uygulanması]
Veya $ F (A, B, C) = 1.A + BC $ [Hakimiyet Yasasını Uygulama]
Veya $ F (A, B, C) = A + BC $ [Hakimiyet Yasasını Uygulama]
Yani, $ F (A, B, C) = A + BC $ küçültülmüş formdur.
Karnaugh Haritaları
Maurice Karnaughin tarafından 1953'te sunulan Karnaugh haritası (K-haritası), boole cebri ifadelerini basitleştirmek için kullanılan bir doğruluk tablosunun ızgaraya benzer bir temsilidir. Bir Karnaugh haritasının farklı konumlarda sıfır ve bir girişi vardır. Boole ifadelerinin ortak faktörlerle birlikte gruplandırılmasını sağlar ve istenmeyen değişkenleri ifadeden çıkarır. Bir K-haritasında, dikey veya yatay bir hücre sınırını geçmek her zaman yalnızca bir değişkenin değişikliğidir.
örnek 1
Aşağıda keyfi bir doğruluk tablosu alınmıştır -
| Bir | B | A operasyonu B |
|---|---|---|
| 0 | 0 | w |
| 0 | 1 | x |
| 1 | 0 | y |
| 1 | 1 | z |
Şimdi yukarıdaki doğruluk tablosu için bir k-haritası yapacağız -

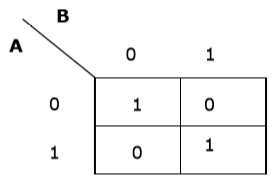
Örnek 2
Şimdi - AB + A'B 'ifadesi için bir K-haritası yapacağız.
K-map Kullanarak Basitleştirme
K-haritası, bitişik hücreleri tek bir terim halinde birleştirerek Boole ifadelerinin basitleştirilmesi için bazı kurallar kullanır. Kurallar aşağıda açıklanmıştır -
Rule 1 - Sıfır içeren hiçbir hücre gruplanamaz.
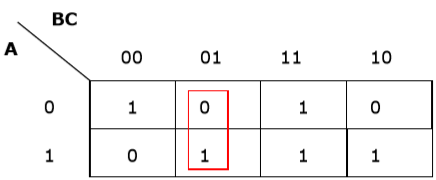
Yanlış gruplama
Rule 2 - Gruplar 2n hücre içermelidir (1'den başlayarak n).
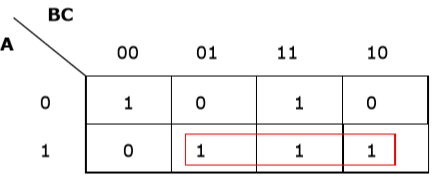
Yanlış gruplama
Rule 3 - Gruplama yatay veya dikey olmalı, ancak çapraz olmamalıdır.
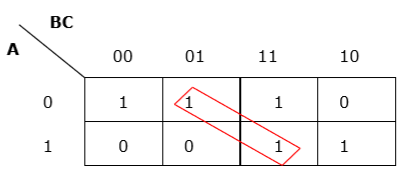
Yanlış çapraz gruplama
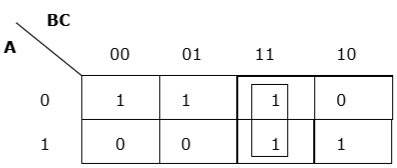
Uygun dikey gruplama
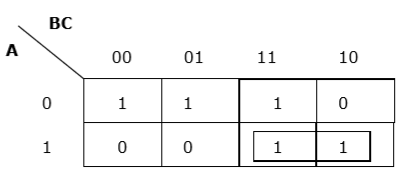
Uygun yatay gruplama
Rule 4 - Gruplar olabildiğince geniş kapsamlı olmalıdır.
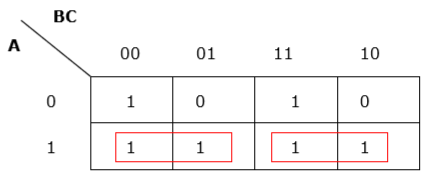
Yetersiz gruplama
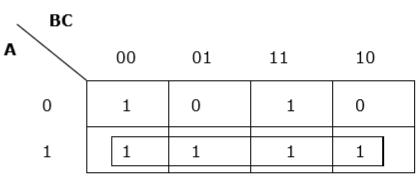
Doğru gruplama
Rule 5 - Herhangi bir hücreden 1 tanesi başka bir hücre ile gruplanamazsa, kendisi bir grup olarak hareket edecektir.
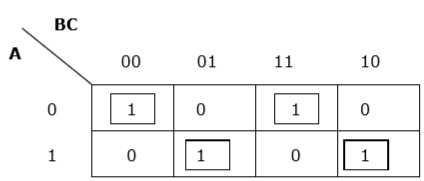
Doğru gruplama
Rule 6 - Gruplar çakışabilir, ancak mümkün olduğunca az grup olmalıdır.
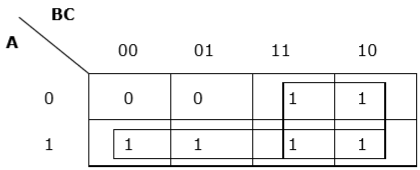
Doğru gruplama
Rule 7 - En soldaki hücre / hücreler, en sağdaki hücre / hücreler ile gruplanabilir ve en üstteki hücre / hücreler, en alttaki hücre / hücreler ile gruplanabilir.
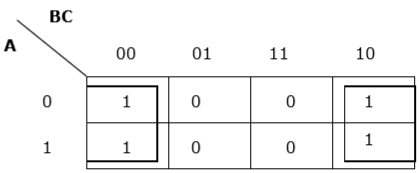
Doğru gruplama
Sorun
K-haritasını kullanarak aşağıdaki Boole ifadesini simge durumuna küçültün -
$$ F (A, B, C) = A'BC + A'BC '+ AB'C' + AB'C $$
Çözüm
Her terim k haritasına yerleştirilir ve aşağıdakileri elde ederiz -
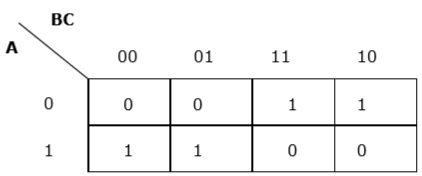
F (A, B, C) için K-haritası
Şimdi 1'in hücrelerini yukarıda belirtilen kurallara göre gruplayacağız -
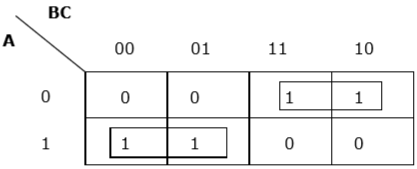
F (A, B, C) için K-haritası
$ A'B $ ve $ AB '$ olarak adlandırılan iki grubumuz var. Dolayısıyla, $ F (A, B, C) = A'B + AB '= A \ oplus B $. Küçültülmüş formdur.