Ayrık Matematik - Hızlı Kılavuz
Matematik genel olarak iki kategoriye ayrılabilir -
Continuous Mathematics- Sürekli sayı doğrusuna veya gerçek sayılara dayanır. Herhangi iki sayı arasında neredeyse her zaman sonsuz bir sayı kümesi olduğu gerçeğiyle karakterizedir. Örneğin, sürekli matematikteki bir fonksiyon, kesintisiz bir eğri ile çizilebilir.
Discrete Mathematics- Farklı değerler içerir; yani herhangi iki nokta arasında sayılabilir sayıda puan vardır. Örneğin, sonlu bir nesne kümesine sahipsek, işlev, bu nesnelere sahip sıralı çiftlerin bir listesi olarak tanımlanabilir ve bu çiftlerin tam bir listesi olarak sunulabilir.
Ayrık Matematikte Konular
Kesikli Matematiğin belirli bir dalı olmasa da, bu konuyla ilgili herhangi bir çalışmada aşağıdaki konular hemen hemen her zaman ele alınır -
- Kümeler, İlişkiler ve Fonksiyonlar
- Matematiksel Mantık
- Grup teorisi
- Sayma Teorisi
- Probability
- Matematiksel Tümevarım ve Tekrarlama İlişkileri
- Grafik teorisi
- Trees
- Boole Cebri
Bu eğitimin sonraki bölümlerinde bu kavramların her birini tartışacağız.
Alman matematikçi G. CantorKümeler kavramını tanıttı. Kümeyi, belirli kurallar veya tanımlarla seçilen belirli ve ayırt edilebilir nesnelerin bir koleksiyonu olarak tanımlamıştı.
Setteori, sayma teorisi, ilişkiler, grafik teorisi ve sonlu durum makineleri gibi diğer birçok çalışma alanının temelini oluşturur. Bu bölümde, farklı yönlerini ele alacağız.Set Theory.
Küme - Tanım
Küme, farklı öğelerin sıralanmamış bir koleksiyonudur. Bir küme, elemanları küme ayracı kullanılarak listelenerek açık bir şekilde yazılabilir. Elemanların sırası değiştirilirse veya bir kümenin herhangi bir elemanı tekrarlanırsa, kümede herhangi bir değişiklik yapmaz.
Bazı Set Örnekleri
- Tüm pozitif tam sayılar kümesi
- Güneş sistemindeki tüm gezegenlerin bir kümesi
- Hindistan'daki tüm eyaletler kümesi
- Alfabenin tüm küçük harflerinden oluşan bir set
Bir Kümenin Temsili
Kümeler iki şekilde temsil edilebilir -
- Kadro veya Tablo Form
- Oluşturucu Gösterimini Ayarla
Kadro veya Tablo Form
Set, onu oluşturan tüm unsurların listelenmesiyle temsil edilir. Öğeler kaşlı ayraç içine alınır ve virgülle ayrılır.
Example 1 - İngiliz alfabesinde sesli harf seti, $A = \lbrace a,e,i,o,u \rbrace$
Example 2 - 10'dan küçük tek sayılar kümesi, $B = \lbrace 1,3,5,7,9 \rbrace$
Oluşturucu Gösterimini Ayarla
Küme, kümenin elemanlarının ortak olarak sahip olduğu bir özellik belirtilerek tanımlanır. Set şu şekilde tanımlanmıştır:$A = \lbrace x : p(x) \rbrace$
Example 1 - Set $\lbrace a,e,i,o,u \rbrace$ şu şekilde yazılmıştır -
$A = \lbrace x : \text{x is a vowel in English alphabet} \rbrace$
Example 2 - Set $\lbrace 1,3,5,7,9 \rbrace$ şu şekilde yazılmıştır -
$B = \lbrace x : 1 \le x \lt 10 \ and\ (x \% 2) \ne 0 \rbrace$
Bir x öğesi herhangi bir S kümesinin üyesi ise, ile gösterilir $x \in S$ ve bir y öğesi S kümesinin bir üyesi değilse, ile gösterilir $y \notin S$.
Example- eğer$S = \lbrace1, 1.2, 1.7, 2\rbrace , 1 \in S$ fakat $1.5 \notin S$
Bazı Önemli Setler
N - tüm doğal sayılar kümesi = $\lbrace1, 2, 3, 4, .....\rbrace$
Z - tüm tam sayılar kümesi = $\lbrace....., -3, -2, -1, 0, 1, 2, 3, .....\rbrace$
Z+ - tüm pozitif tam sayılar kümesi
Q - tüm rasyonel sayılar kümesi
R - tüm gerçek sayılar kümesi
W - tüm tam sayılar kümesi
Bir Kümenin Asalitesi
Bir S kümesinin kardinalitesi ile gösterilen $|S|$, kümenin eleman sayısıdır. Sayı aynı zamanda kardinal sayı olarak da adlandırılır. Bir kümenin sonsuz sayıda öğesi varsa, önemi$\infty$.
Example - $|\lbrace 1, 4, 3, 5 \rbrace | = 4, | \lbrace 1, 2, 3, 4, 5, \dots \rbrace | = \infty$
X ve Y olmak üzere iki küme varsa,
$|X| = |Y|$aynı kardinaliteye sahip iki X ve Y kümesini belirtir. X'teki öğelerin sayısı Y'deki öğelerin sayısına tam olarak eşit olduğunda ortaya çıkar. Bu durumda, X'ten Y'ye bir "f" önyargılı işlevi vardır.
$|X| \le |Y|$, X'in kardinalitesinin Y'nin kardinalitesini ayarlamaktan küçük veya ona eşit olduğunu belirtir. X'teki elemanların sayısı Y'ninkinden az veya ona eşit olduğunda meydana gelir. Burada, X'ten Y'ye bir 'f' enjeksiyon fonksiyonu vardır.
$|X| \lt |Y|$, X'in kardinalitesinin, setin Y'nin kardinalitesinden daha az olduğunu belirtir. X'teki elemanların sayısı Y'ninkinden daha az olduğunda ortaya çıkar. Burada, X'ten Y'ye 'f' işlevi enjeksiyon işlevidir, ancak önyargılı değildir.
$If\ |X| \le |Y|$ ve $|X| \ge |Y|$ sonra $|X| = |Y|$. X ve Y kümeleri genellikle eşdeğer kümeler olarak adlandırılır.
Set Türleri
Setler birçok türe ayrılabilir. Bazıları sonlu, sonsuz, alt küme, evrensel, uygun, tekli küme vb.
Sınırlı set
Belirli sayıda eleman içeren bir küme, sonlu küme olarak adlandırılır.
Example - $S = \lbrace x \:| \:x \in N$ ve $70 \gt x \gt 50 \rbrace$
Sonsuz Küme
Sonsuz sayıda eleman içeren bir kümeye sonsuz küme denir.
Example - $S = \lbrace x \: | \: x \in N $ ve $ x \gt 10 \rbrace$
Alt küme
Bir X kümesi, Y kümesinin bir alt kümesidir ( $X \subseteq Y$) eğer X'in her öğesi Y kümesinin bir öğesiyse.
Example 1 - Bırak, $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ ve $Y = \lbrace 1, 2 \rbrace$. Burada Y kümesi, X kümesinin bir alt kümesidir, çünkü Y kümesinin tüm elemanları X kümesinde yer alır. Dolayısıyla yazabiliriz.$Y \subseteq X$.
Example 2 - Bırak, $X = \lbrace 1, 2, 3 \rbrace$ ve $Y = \lbrace 1, 2, 3 \rbrace$. Burada Y kümesi, X kümesinin bir alt kümesidir (uygun bir alt küme değildir), çünkü Y kümesinin tüm elemanları X kümesinde yer alır. Dolayısıyla yazabiliriz.$Y \subseteq X$.
Uygun altküme
"Uygun alt küme" terimi "alt küme" olarak tanımlanabilir ancak eşit değildir. Bir X Seti, Y kümesinin uygun bir alt kümesidir ($ X \subset Y $) eğer X'in her elemanı Y kümesinin bir elemanıysa ve $|X| \lt |Y|$.
Example - Bırak, $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ ve $Y = \lbrace 1, 2 \rbrace$. İşte set$Y \subset X$ çünkü tüm unsurlar $Y$ içinde yer almaktadır $X$ çok ve $X$ en az bir öğeye sahip olduğundan daha fazla $Y$.
Evrensel set
Belirli bir bağlam veya uygulamadaki tüm öğelerin bir koleksiyonudur. Bu bağlam veya uygulamadaki tüm kümeler, esasen bu evrensel kümenin alt kümeleridir. Evrensel kümeler şu şekilde temsil edilir:$U$.
Example - Tanımlayabiliriz $U$dünyadaki tüm hayvanların kümesi olarak. Bu durumda, tüm memeliler kümesi bir alt kümesidir$U$, tüm balıkların bir alt kümesidir $U$, tüm böceklerin bir alt kümesidir $U$, ve bunun gibi.
Boş Küme veya Boş Küme
Boş bir küme hiçbir öğe içermez. İle gösterilir$\emptyset$. Boş bir kümedeki eleman sayısı sonlu olduğundan, boş küme sonlu bir kümedir. Boş küme veya boş kümenin önem derecesi sıfırdır.
Example - $S = \lbrace x \:| \: x \in N$ ve $7 \lt x \lt 8 \rbrace = \emptyset$
Singleton Set veya Unit Set
Tekli set veya birim seti yalnızca bir öğe içerir. Tekil bir set şu şekilde gösterilir:$\lbrace s \rbrace$.
Example - $S = \lbrace x \:| \:x \in N,\ 7 \lt x \lt 9 \rbrace$ = $\lbrace 8 \rbrace$
Eşit Küme
İki set aynı öğeleri içeriyorsa, eşit oldukları söylenir.
Example - eğer $A = \lbrace 1, 2, 6 \rbrace$ ve $B = \lbrace 6, 1, 2 \rbrace$, A kümesinin her öğesi B kümesinin bir öğesi ve B kümesinin her öğesi A kümesinin bir öğesi olduğundan eşittirler.
Eşdeğer Set
İki kümenin kardinaliteleri aynıysa, bunlara eşdeğer kümeler denir.
Example - eğer $A = \lbrace 1, 2, 6 \rbrace$ ve $B = \lbrace 16, 17, 22 \rbrace$A'nın kardinalitesi B'nin kardinalitesine eşit olduğu için eşdeğerdirler. $|A| = |B| = 3$
Çakışan Küme
En az bir ortak öğesi olan iki kümeye örtüşen kümeler denir.
Örtüşen kümeler durumunda -
$n(A \cup B) = n(A) + n(B) - n(A \cap B)$
$n(A \cup B) = n(A - B) + n(B - A) + n(A \cap B)$
$n(A) = n(A - B) + n(A \cap B)$
$n(B) = n(B - A) + n(A \cap B)$
Example - Bırak, $A = \lbrace 1, 2, 6 \rbrace$ ve $B = \lbrace 6, 12, 42 \rbrace$. Ortak bir '6' öğesi vardır, bu nedenle bu kümeler örtüşen kümelerdir.
Ayrık Set
Ortak bir öğeye sahip değillerse, iki A ve B kümesine ayrık kümeler denir. Bu nedenle, ayrık kümeler aşağıdaki özelliklere sahiptir -
$n(A \cap B) = \emptyset$
$n(A \cup B) = n(A) + n(B)$
Example - Bırak, $A = \lbrace 1, 2, 6 \rbrace$ ve $B = \lbrace 7, 9, 14 \rbrace$tek bir ortak öğe yoktur, dolayısıyla bu kümeler örtüşen kümelerdir.
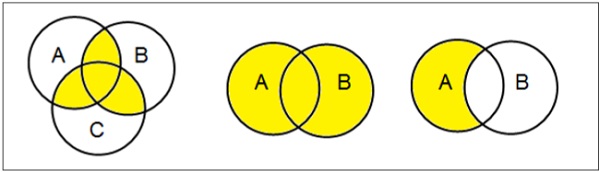
Venn şemaları
1880'de John Venn tarafından icat edilen Venn diyagramı, farklı matematiksel kümeler arasındaki tüm olası mantıksal ilişkileri gösteren şematik bir diyagramdır.
Examples
İşlemleri Ayarla
Set İşlemleri arasında Set Union, Set Intersection, Set Difference, Complement of Set ve Cartesian Product bulunur.
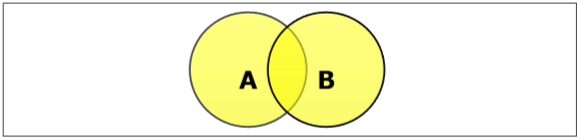
Birlik Ayarla
A ve B kümelerinin birleşimi (ile gösterilir $A \cup B$), A'da, B'de veya hem A hem de B'de bulunan öğeler kümesidir. Dolayısıyla, $A \cup B = \lbrace x \:| \: x \in A\ OR\ x \in B \rbrace$.
Example - eğer $A = \lbrace 10, 11, 12, 13 \rbrace$ ve B = $\lbrace 13, 14, 15 \rbrace$, sonra $A \cup B = \lbrace 10, 11, 12, 13, 14, 15 \rbrace$. (Ortak öğe yalnızca bir kez oluşur)
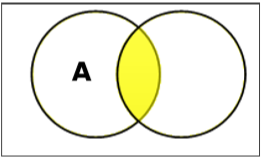
Kesişimi Ayarla
A ve B kümelerinin kesişimi (ile gösterilir $A \cap B$) hem A hem de B'de bulunan öğeler kümesidir. Dolayısıyla, $A \cap B = \lbrace x \:|\: x \in A\ AND\ x \in B \rbrace$.
Example - eğer $A = \lbrace 11, 12, 13 \rbrace$ ve $B = \lbrace 13, 14, 15 \rbrace$, sonra $A \cap B = \lbrace 13 \rbrace$.
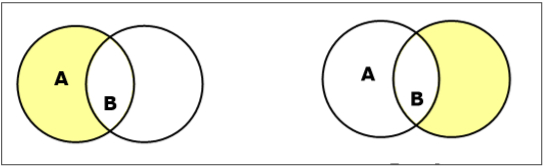
Farkı Ayarla / Göreli Tamamlayıcı
A ve B kümelerinin küme farkı (ile gösterilir $A – B$), yalnızca A'da bulunan ancak B'de olmayan öğeler kümesidir. Dolayısıyla, $A - B = \lbrace x \:| \: x \in A\ AND\ x \notin B \rbrace$.
Example - eğer $A = \lbrace 10, 11, 12, 13 \rbrace$ ve $B = \lbrace 13, 14, 15 \rbrace$, sonra $(A - B) = \lbrace 10, 11, 12 \rbrace$ ve $(B - A) = \lbrace 14, 15 \rbrace$. Burada görebiliriz$(A - B) \ne (B - A)$
Bir Setin Tamamlayıcısı
Bir A kümesinin tamamlayıcısı (ile gösterilir $A’$) A kümesinde bulunmayan öğeler kümesidir. Dolayısıyla, $A' = \lbrace x | x \notin A \rbrace$.
Daha spesifik olarak, $A'= (U - A)$ nerede $U$ tüm nesneleri içeren evrensel bir kümedir.
Example - eğer $A = \lbrace x \:| \: x\ \: {belongs\: to\: set\: of\: odd \:integers} \rbrace$ sonra $A' = \lbrace y\: | \: y\ \: {does\: not\: belong\: to\: set\: of\: odd\: integers } \rbrace$
Kartezyen Ürün / Çapraz Ürün
N sayıda kümenin kartezyen çarpımı $A_1, A_2, \dots A_n$ olarak belirtildi $A_1 \times A_2 \dots \times A_n$ olası tüm sıralı çiftler olarak tanımlanabilir $(x_1, x_2, \dots x_n)$ nerede $x_1 \in A_1, x_2 \in A_2, \dots x_n \in A_n$
Example - İki set alırsak $A = \lbrace a, b \rbrace$ ve $B = \lbrace 1, 2 \rbrace$,
A ve B'nin Kartezyen çarpımı şu şekilde yazılır - $A \times B = \lbrace (a, 1), (a, 2), (b, 1), (b, 2)\rbrace$
B ve A'nın Kartezyen çarpımı şu şekilde yazılır - $B \times A = \lbrace (1, a), (1, b), (2, a), (2, b)\rbrace$
Gücü ayarla
Bir S kümesinin güç kümesi, boş küme dahil tüm S alt kümelerinin kümesidir. Kardinalite n'nin bir S kümesinin bir güç kümesinin kardinalitesi,$2^n$. Güç seti şu şekilde gösterilir:$P(S)$.
Example −
Bir set için $S = \lbrace a, b, c, d \rbrace$ alt kümeleri hesaplayalım -
0 öğeli alt kümeler - $\lbrace \emptyset \rbrace$ (boş küme)
1 öğeli alt kümeler - $\lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace$
2 öğeli alt kümeler - $\lbrace a, b \rbrace, \lbrace a,c \rbrace, \lbrace a, d \rbrace, \lbrace b, c \rbrace, \lbrace b,d \rbrace,\lbrace c,d \rbrace$
3 öğeli alt kümeler - $\lbrace a ,b, c\rbrace,\lbrace a, b, d \rbrace, \lbrace a,c,d \rbrace,\lbrace b,c,d \rbrace$
4 öğeli alt kümeler - $\lbrace a, b, c, d \rbrace$
Dolayısıyla $P(S)=$
$\lbrace \quad \lbrace \emptyset \rbrace, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace, \lbrace a,b \rbrace, \lbrace a,c \rbrace, \lbrace a,d \rbrace, \lbrace b,c \rbrace, \lbrace b,d \rbrace, \lbrace c,d \rbrace, \lbrace a,b,c \rbrace, \lbrace a,b,d \rbrace, \lbrace a,c,d \rbrace, \lbrace b,c,d \rbrace, \lbrace a,b,c,d \rbrace \quad \rbrace$
$| P(S) | = 2^4 = 16$
Note - Boş bir setin güç seti de boş bir settir.
$| P (\lbrace \emptyset \rbrace) | = 2^0 = 1$
Bir Setin Bölümlenmesi
Bir kümenin bölümlenmesi, örneğin S , n ayrık alt kümeden oluşan bir koleksiyondur , diyelim ki$P_1, P_2, \dots P_n$ aşağıdaki üç koşulu karşılayan -
$P_i$ boş küme içermiyor.
$\lbrack P_i \ne \lbrace \emptyset \rbrace\ for\ all\ 0 \lt i \le n \rbrack$
Alt kümelerin birleşimi, orijinal kümenin tamamına eşit olmalıdır.
$\lbrack P_1 \cup P_2 \cup \dots \cup P_n = S \rbrack$
Herhangi iki farklı kümenin kesişimi boştur.
$\lbrack P_a \cap P_b = \lbrace \emptyset \rbrace,\ for\ a \ne b\ where\ n \ge a,\: b \ge 0 \rbrack$
Example
İzin Vermek $S = \lbrace a, b, c, d, e, f, g, h \rbrace$
Olası bir bölümleme $\lbrace a \rbrace, \lbrace b, c, d \rbrace, \lbrace e, f, g, h \rbrace$
Başka bir olası bölümleme $\lbrace a, b \rbrace, \lbrace c, d \rbrace, \lbrace e, f, g, h \rbrace$
Bell Numaraları
Çan sayıları, bir kümeyi bölümleme yollarının sayısını verir. İle gösterilirler$B_n$ burada n, kümenin önemidir.
Example -
İzin Vermek $S = \lbrace 1, 2, 3\rbrace$, $n = |S| = 3$
Alternatif bölümler -
1. $\emptyset , \lbrace 1, 2, 3 \rbrace$
2. $\lbrace 1 \rbrace , \lbrace 2, 3 \rbrace$
3. $\lbrace 1, 2 \rbrace , \lbrace 3 \rbrace$
4. $\lbrace 1, 3 \rbrace , \lbrace 2 \rbrace$
5. $\lbrace 1 \rbrace , \lbrace 2 \rbrace , \lbrace 3 \rbrace$
Bu nedenle $B_3 = 5$
Ne zaman setler tartışılırsa, setlerin unsurları arasındaki ilişki ortaya çıkan bir sonraki şeydir. Relations aynı kümedeki nesneler arasında veya iki veya daha fazla kümenin nesneleri arasında var olabilir.
Tanım ve Özellikler
X kümesinden y'ye ikili ilişki R (şu şekilde yazılır: $xRy$ veya $R(x,y)$), Kartezyen ürünün bir alt kümesidir $x \times y$. Sıralı G çifti tersine çevrilirse, ilişki de değişir.
Genellikle kümeler arasında n-ary ilişki R $A_1, \dots ,\ and\ A_n$ n-ary ürünün bir alt kümesidir $A_1 \times \dots \times A_n$. Bir R ilişkisinin minimum kardinalitesi Sıfırdır ve maksimum$n^2$ bu durumda.
Tek bir A kümesindeki bir ikili ilişki R, bir alt kümesidir $A \times A$.
Sırasıyla m ve n kardinalitelerine sahip iki ayrı küme için, A ve B için, A'dan B'ye bir R ilişkisinin maksimum kardinalitesi mn'dir .
Etki Alanı ve Aralık
İki A ve B kümesi varsa ve R ilişkisi sıra çiftine (x, y) sahipse, o zaman -
domain R, Dom (R), küme $\lbrace x \:| \: (x, y) \in R \:for\: some\: y\: in\: B \rbrace$
range R, Ran (R) kümesidir $\lbrace y\: |\: (x, y) \in R \:for\: some\: x\: in\: A\rbrace$
Örnekler
İzin Vermek, $A = \lbrace 1, 2, 9 \rbrace $ ve $ B = \lbrace 1, 3, 7 \rbrace$
Durum 1 - Eğer R ilişkisi 'eşitse' o zaman $R = \lbrace (1, 1), (3, 3) \rbrace$
Dom (R) = $\lbrace 1, 3 \rbrace , Ran(R) = \lbrace 1, 3 \rbrace$
Durum 2 - R ilişkisi 'küçüktür' ise o zaman $R = \lbrace (1, 3), (1, 7), (2, 3), (2, 7) \rbrace$
Dom (R) = $\lbrace 1, 2 \rbrace , Ran(R) = \lbrace 3, 7 \rbrace$
Durum 3 - R ilişkisi 'büyükse' o zaman $R = \lbrace (2, 1), (9, 1), (9, 3), (9, 7) \rbrace$
Dom (R) = $\lbrace 2, 9 \rbrace , Ran(R) = \lbrace 1, 3, 7 \rbrace$
İlişkilerin Grafik Kullanılarak Gösterimi
Bir ilişki, yönlendirilmiş bir grafik kullanılarak temsil edilebilir.
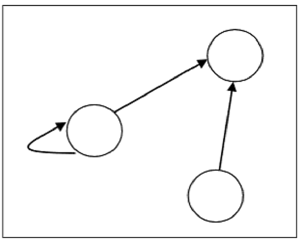
Grafikteki köşe sayısı, ilişkinin tanımlandığı kümedeki öğe sayısına eşittir. R ilişkisindeki her bir sıralı çift (x, y) için, 'x' tepe noktasından 'y' tepe noktasına yönlendirilmiş bir kenar olacaktır. Sıralı bir çift (x, x) varsa, 'x' tepe noktasında kendi kendine döngü olacaktır.
Varsayalım, bir ilişki var $R = \lbrace (1, 1), (1,2), (3, 2) \rbrace$ sette $S = \lbrace 1, 2, 3 \rbrace$aşağıdaki grafikle gösterilebilir -
İlişki Türleri
Empty Relation X ve Y kümeleri arasında veya E'de boş küme $\emptyset$
Full Relation X ve Y kümeleri arasında kümedir $X \times Y$
Identity Relation sette X settir $\lbrace (x, x) | x \in X \rbrace$
Bir R ilişkisinin Ters İlişkisi R 'şu şekilde tanımlanır - $R' = \lbrace (b, a) | (a, b) \in R \rbrace$
Example - eğer $R = \lbrace (1, 2), (2, 3) \rbrace$ sonra $R' $ olacak $\lbrace (2, 1), (3, 2) \rbrace$
A kümesinde bir R ilişkisi denir Reflexive Eğer $\forall a \in A$ a (aRa muhafazaları) ile ilgilidir
Example - İlişki $R = \lbrace (a, a), (b, b) \rbrace$ sette $X = \lbrace a, b \rbrace$ dönüşlüdür.
A kümesinde bir R ilişkisi denir Irreflexive Eğer hayırsa $a \in A$ a ile ilgilidir (aRa tutmaz).
Example - İlişki $R = \lbrace (a, b), (b, a) \rbrace$ sette $X = \lbrace a, b \rbrace$ yansımasızdır.
A kümesinde bir R ilişkisi denir Symmetric Eğer $xRy$ ima eder $yRx$, $\forall x \in A$ ve $\forall y \in A$.
Example - İlişki $R = \lbrace (1, 2), (2, 1), (3, 2), (2, 3) \rbrace$ sette $A = \lbrace 1, 2, 3 \rbrace$ simetriktir.
A kümesinde bir R ilişkisi denir Anti-Symmetric Eğer $xRy$ ve $yRx$ ima eder $x = y \: \forall x \in A$ ve $\forall y \in A$.
Example - İlişki $R = \lbrace (x, y)\to N |\:x \leq y \rbrace$ anti-simetriktir çünkü $x \leq y$ ve $y \leq x$ ima eder $x = y$.
A kümesinde bir R ilişkisi denir Transitive Eğer $xRy$ ve $yRz$ ima eder $xRz, \forall x,y,z \in A$.
Example - İlişki $R = \lbrace (1, 2), (2, 3), (1, 3) \rbrace$ sette $A = \lbrace 1, 2, 3 \rbrace$ geçişlidir.
Bir ilişki bir Equivalence Relation dönüşlü, simetrik ve geçişli ise.
Example - İlişki $R = \lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \rbrace$ sette $A = \lbrace 1, 2, 3 \rbrace$ dönüşlü, simetrik ve geçişli olduğu için bir eşdeğerlik ilişkisidir.
Bir Functionbir kümenin her bir öğesine, ilişkili bir kümenin tam olarak bir öğesini atar. Fonksiyonlar, uygulamalarını, algoritmaların hesaplama karmaşıklığının temsili, nesneleri sayma, dizilerin ve dizelerin incelenmesi gibi çeşitli alanlarda bulurlar. Bu bölümün üçüncü ve son bölümü, işlevlerin önemli yönlerini vurgulamaktadır.
İşlev - Tanım
Bir işlev veya eşleme ( $f: X \rightarrow Y$), bir X kümesinin öğelerinden başka bir Y kümesinin öğeleriyle bir ilişkidir (X ve Y, boş olmayan kümelerdir). X, Domain olarak adlandırılır ve Y, 'f' fonksiyonunun Codomain olarak adlandırılır.
'F' fonksiyonu, X ve Y üzerindeki bir ilişkidir, öyle ki her biri için $x \in X$benzersiz bir $y \in Y$ öyle ki $(x,y) \in R$. 'x' ön görüntü olarak adlandırılır ve 'y' f işlevinin görüntüsü olarak adlandırılır.
Bir işlev bire bir veya çoktan bire olabilir ancak birden çoğa olamaz.
Enjeksiyon / Bire bir işlev
Bir işlev $f: A \rightarrow B$ enjekte veya bire bir işlevdir. $b \in B$en fazla bir tane var $a \in A$ öyle ki $f(s) = t$.
Bu bir işlev anlamına gelir f eğer enjekte edicidir $a_1 \ne a_2$ ima eder $f(a1) \ne f(a2)$.
Misal
$f: N \rightarrow N, f(x) = 5x$ enjekte edici.
$f: N \rightarrow N, f(x) = x^2$ enjekte edici.
$f: R\rightarrow R, f(x) = x^2$ enjekte edici değil $(-x)^2 = x^2$
Surjective / Onto işlevi
Bir işlev $f: A \rightarrow B$f imgesi aralığına eşitse, örten (üzerine). Eşit olarak, her biri için$b \in B$, biraz var $a \in A$ öyle ki $f(a) = b$. Bu, B'deki herhangi bir y için, A'da bir miktar x olduğu anlamına gelir, öyle ki$y = f(x)$.
Misal
$f : N \rightarrow N, f(x) = x + 2$ örten.
$f : R \rightarrow R, f(x) = x^2$ karesi negatif olan bir gerçek sayı bulamadığımız için, örten değildir.
Bijective / Bire Bir Muhabir
Bir işlev $f: A \rightarrow B$ önyargılı veya bire bir muhabir ise, ancak ve ancak f hem enjekte edici hem de kuşatıcıdır.
Sorun
Bir işlev olduğunu kanıtlayın $f: R \rightarrow R$ tarafından tanımlandı $f(x) = 2x – 3$ önyargılı bir işlevdir.
Explanation - Bu işlevin hem aşılayıcı hem de kuşatıcı olduğunu kanıtlamalıyız.
Eğer $f(x_1) = f(x_2)$, sonra $2x_1 – 3 = 2x_2 – 3 $ ve bunu ima ediyor $x_1 = x_2$.
Dolayısıyla, f injective.
Buraya, $2x – 3= y$
Yani, $x = (y+5)/3$ hangisi R'ye ait ve $f(x) = y$.
Dolayısıyla, f surjective.
Dan beri f ikiside surjective ve injective, söyleyebiliriz f dır-dir bijective.
Bir Fonksiyonun Tersi
inverse bire bir karşılık gelen işlevin $f : A \rightarrow B$işlev $g : B \rightarrow A$, aşağıdaki mülke sahip olmak -
$f(x) = y \Leftrightarrow g(y) = x$
F fonksiyonu denir invertibleters fonksiyonu g varsa.
Misal
Bir işlev $f : Z \rightarrow Z, f(x)=x+5$ters işlevi olduğundan ters çevrilebilir $ g : Z \rightarrow Z, g(x)= x-5$.
Bir işlev $f : Z \rightarrow Z, f(x)=x^2$ tersine çevrilemez çünkü bu bire bir değildir, çünkü $(-x)^2=x^2$.
Fonksiyonların Bileşimi
İki fonksiyon $f: A \rightarrow B$ ve $g: B \rightarrow C$ bir kompozisyon vermek için bestelenebilir $g o f$. Bu, A'dan C'ye bir fonksiyondur.$(gof)(x) = g(f(x))$
Misal
İzin Vermek $f(x) = x + 2$ ve $g(x) = 2x + 1$bul $( f o g)(x)$ ve $( g o f)(x)$.
Çözüm
$(f o g)(x) = f (g(x)) = f(2x + 1) = 2x + 1 + 2 = 2x + 3$
$(g o f)(x) = g (f(x)) = g(x + 2) = 2 (x+2) + 1 = 2x + 5$
Dolayısıyla $(f o g)(x) \neq (g o f)(x)$
Kompozisyonla İlgili Bazı Gerçekler
F ve g bire bir ise, fonksiyon $(g o f)$ aynı zamanda bire bir.
F ve g üstündeyse, işlev $(g o f)$ ayrıca üzerindedir.
Kompozisyon her zaman birleşik özelliği taşır, ancak değişme özelliği taşımaz.
Matematiksel mantık kuralları, matematiksel ifadeleri akıl yürütme yöntemlerini belirtir. Yunan filozof Aristo, mantıksal akıl yürütmenin öncüsüydü. Mantıksal akıl yürütme, matematiğin ve dolayısıyla bilgisayar biliminin birçok alanı için teorik temel sağlar. Bilgisayar bilimlerinde, bilgi işlem makinelerinin tasarımı, yapay zeka, programlama dilleri için veri yapılarının tanımlanması gibi birçok pratik uygulamaya sahiptir.
Propositional Logicdoğruluk değerlerinin "doğru" ve "yanlış" atanabileceği ifadelerle ilgilenir. Amaç, bu ifadeleri tek tek veya bileşik bir şekilde analiz etmektir.
Edat Mantığı - Tanım
Bir önerme, bir doğruluk değeri "doğru" veya bir doğruluk değeri "yanlış" olan bildirimsel ifadelerin bir koleksiyonudur. Bir önerme, önermesel değişkenlerden ve bağlayıcılardan oluşur. Önerme değişkenlerini büyük harflerle (A, B, vb.) Gösteririz. Bağlayıcılar önermesel değişkenleri bağlar.
Bazı Önerme örnekleri aşağıda verilmiştir -
- "İnsan Ölümlüdür", "DOĞRU" gerçek değerini döndürür
- "12 + 9 = 3 - 2", "FALSE" doğruluk değerini döndürür
Aşağıdakiler bir Önerme değildir -
"A, 2'den küçüktür". Çünkü belirli bir A değeri vermedikçe, ifadenin doğru mu yanlış mı olduğunu söyleyemeyiz.
Bağlantılar
Önerme mantığında genellikle şu beş bağlantı kullanırız:
VEYA ($\lor$)
VE ($\land$)
Olumsuz / DEĞİL ($\lnot$)
Çıkarım / eğer-öyleyse ($\rightarrow$)
Ancak ve ancak ($\Leftrightarrow$).
OR ($\lor$) - A ve B önermelerinin OR işlemi (şu şekilde yazılır: $A \lor B$) önermesel değişken A veya B'nin en azından herhangi biri doğruysa doğrudur.
Doğruluk tablosu aşağıdaki gibidir -
| Bir | B | A ∨ B |
|---|---|---|
| Doğru | Doğru | Doğru |
| Doğru | Yanlış | Doğru |
| Yanlış | Doğru | Doğru |
| Yanlış | Yanlış | Yanlış |
AND ($\land$) - A ve B önermelerinin (şu şekilde yazılır) AND işlemi $A \land B$) hem önermesel değişken A hem de B doğruysa doğrudur.
Doğruluk tablosu aşağıdaki gibidir -
| Bir | B | A ∧ B |
|---|---|---|
| Doğru | Doğru | Doğru |
| Doğru | Yanlış | Yanlış |
| Yanlış | Doğru | Yanlış |
| Yanlış | Yanlış | Yanlış |
Negation ($\lnot$) - A önermesinin olumsuzlanması (şu şekilde yazılır: $\lnot A$), A doğru olduğunda yanlış ve A yanlış olduğunda doğrudur.
Doğruluk tablosu aşağıdaki gibidir -
| Bir | ¬ A |
|---|---|
| Doğru | Yanlış |
| Yanlış | Doğru |
Implication / if-then ($\rightarrow$) - Bir ima $A \rightarrow B$"eğer A ise, sonra B" önermesidir. A doğruysa ve B yanlışsa yanlıştır. Geri kalan durumlar doğrudur.
Doğruluk tablosu aşağıdaki gibidir -
| Bir | B | A → B |
|---|---|---|
| Doğru | Doğru | Doğru |
| Doğru | Yanlış | Yanlış |
| Yanlış | Doğru | Doğru |
| Yanlış | Yanlış | Doğru |
If and only if ($ \Leftrightarrow $) - $A \Leftrightarrow B$ p ve q aynı olduğunda, yani her ikisi de yanlış veya her ikisi de doğru olduğunda doğru olan iki koşullu mantıksal bağlayıcıdır.
Doğruluk tablosu aşağıdaki gibidir -
| Bir | B | A ⇔ B |
|---|---|---|
| Doğru | Doğru | Doğru |
| Doğru | Yanlış | Yanlış |
| Yanlış | Doğru | Yanlış |
| Yanlış | Yanlış | Doğru |
Totolojiler
Bir Totoloji, önerme değişkenlerinin her değeri için her zaman doğru olan bir formüldür.
Example - Kanıtla $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ bir totolojidir
Doğruluk tablosu aşağıdaki gibidir -
| Bir | B | A → B | (A → B) ∧ A | [(A → B) ∧ A] → B |
|---|---|---|---|---|
| Doğru | Doğru | Doğru | Doğru | Doğru |
| Doğru | Yanlış | Yanlış | Yanlış | Doğru |
| Yanlış | Doğru | Doğru | Yanlış | Doğru |
| Yanlış | Yanlış | Doğru | Yanlış | Doğru |
Her değerini görebildiğimiz gibi $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ "Doğru" ise bir totolojidir.
Çelişkiler
Bir Çelişki, önerme değişkenlerinin her değeri için her zaman yanlış olan bir formüldür.
Example - Kanıtla $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ bir çelişki
Doğruluk tablosu aşağıdaki gibidir -
| Bir | B | A ∨ B | ¬ A | ¬ B | (¬ A) ∧ (¬ B) | (A ∨ B) ∧ [(¬ A) ∧ (¬ B)] |
|---|---|---|---|---|---|---|
| Doğru | Doğru | Doğru | Yanlış | Yanlış | Yanlış | Yanlış |
| Doğru | Yanlış | Doğru | Yanlış | Doğru | Yanlış | Yanlış |
| Yanlış | Doğru | Doğru | Doğru | Yanlış | Yanlış | Yanlış |
| Yanlış | Yanlış | Yanlış | Doğru | Doğru | Doğru | Yanlış |
Her değerini görebildiğimiz gibi $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ "Yanlış", bir çelişkidir.
Olasılık
Olasılık, önerme değişkenlerinin her değeri için hem bazı doğru hem de bazı yanlış değerler içeren bir formüldür.
Example - Kanıtla $(A \lor B) \land (\lnot A)$ bir olasılık
Doğruluk tablosu aşağıdaki gibidir -
| Bir | B | A ∨ B | ¬ A | (A ∨ B) ∧ (¬ A) |
|---|---|---|---|---|
| Doğru | Doğru | Doğru | Yanlış | Yanlış |
| Doğru | Yanlış | Doğru | Yanlış | Yanlış |
| Yanlış | Doğru | Doğru | Doğru | Doğru |
| Yanlış | Yanlış | Yanlış | Doğru | Yanlış |
Her değerini görebildiğimiz gibi $(A \lor B) \land (\lnot A)$ hem "Doğru" hem de "Yanlış" var, bu bir olasılıktır.
Önerme Eşdeğerleri
Aşağıdaki iki koşuldan herhangi biri geçerliyse, X ve Y iki ifadesi mantıksal olarak eşdeğerdir -
Her bir ifadenin doğruluk tablosu aynı doğruluk değerlerine sahiptir.
İki koşullu ifade $X \Leftrightarrow Y$ bir totolojidir.
Example - Kanıtla $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ eşdeğerdir
1 ile test st yöntemi (Eşleştirme doğruluk tablosu)
| Bir | B | A ∨ B | ¬ (A ∨ B) | ¬ A | ¬ B | [(¬ A) ∧ (¬ B)] |
|---|---|---|---|---|---|---|
| Doğru | Doğru | Doğru | Yanlış | Yanlış | Yanlış | Yanlış |
| Doğru | Yanlış | Doğru | Yanlış | Yanlış | Doğru | Yanlış |
| Yanlış | Doğru | Doğru | Yanlış | Doğru | Yanlış | Yanlış |
| Yanlış | Yanlış | Yanlış | Doğru | Doğru | Doğru | Doğru |
Burada doğruluk değerlerini görebiliriz $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ aynıdır, dolayısıyla ifadeler eşdeğerdir.
2. yöntemle test etme (Çift koşullu)
| Bir | B | ¬ (A ∨ B) | [(¬ A) ∧ (¬ B)] | [¬ (A ∨ B)] ⇔ [(¬ A) ∧ (¬ B)] |
|---|---|---|---|---|
| Doğru | Doğru | Yanlış | Yanlış | Doğru |
| Doğru | Yanlış | Yanlış | Yanlış | Doğru |
| Yanlış | Doğru | Yanlış | Yanlış | Doğru |
| Yanlış | Yanlış | Doğru | Doğru | Doğru |
Gibi $\lbrack \lnot (A \lor B) \rbrack \Leftrightarrow \lbrack (\lnot A ) \land (\lnot B) \rbrack$ bir totolojidir, ifadeler eşdeğerdir.
Ters, Ters ve Kontra-pozitif
Çıkarım / eğer-öyleyse $(\rightarrow)$koşullu ifade olarak da adlandırılır. İki bölümü vardır -
- Hipotez, p
- Sonuç, q
Daha önce belirtildiği gibi, şu şekilde belirtilir: $p \rightarrow q$.
Example of Conditional Statement- "Ödevini yaparsan, cezalandırılmazsın." Burada "ödevini yap" hipotez, p ve "cezalandırılmayacaksın" sonuç, q.
Inverse- Koşullu önermenin tersi, hem hipotezin hem de sonucun olumsuzlanmasıdır. İfade “p ise, q” ise, tersi “p değilse, q değil” olacaktır. Böylece tersi$p \rightarrow q$ dır-dir $ \lnot p \rightarrow \lnot q$.
Example - "Ödevini yaparsan cezalandırılmazsın" ifadesinin tersi "Ödevini yapmazsan cezalandırılırsın" dır.
Converse- Koşullu önermenin tersi, hipotez ve sonucu birbiriyle değiştirerek hesaplanır. Eğer ifade "p ise, o zaman q" ise, tersi "Eğer q ise, sonra p" olacaktır. Tersi$p \rightarrow q$ dır-dir $q \rightarrow p$.
Example - "Ödevini yaparsan cezalandırılmazsın" ifadesinin anlamı "Cezalandırılmazsan ödevini yaparsın".
Contra-positive- Koşulun ters pozitifliği, hipotezin ve ters ifadenin sonucunun değiştirilmesiyle hesaplanır. İfade "p ise, o zaman q" ise, kontra-pozitif "q değilse, p değil" olacaktır. Kontra pozitif$p \rightarrow q$ dır-dir $\lnot q \rightarrow \lnot p$.
Example - "Ödevini yaparsan, cezalandırılmazsın" ın Kontra-pozitif "Cezalandırılırsan ödevini yapmadın" dır.
Dualite İlkesi
Dualite ilkesi, herhangi bir doğru ifade için, sendikaları kesişimlere (ve tersi) değiştirerek ve Evrensel kümeyi Null kümeye (ve tersi) değiştirerek elde edilen ikili ifadenin de doğru olduğunu belirtir. Herhangi bir ifadenin ikilisi ifadenin kendisiyse, söylenirself-dual Beyan.
Example - İkili $(A \cap B ) \cup C$ dır-dir $(A \cup B) \cap C$
Normal Formlar
Herhangi bir önermeyi iki normal forma dönüştürebiliriz -
- Birleşik normal form
- Ayrık normal form
Birleşik Normal Form
Bir bileşik ifade, OR'lerle bağlantılı değişkenler arasında (değişkenlerin olumsuzlanması dahil) VE'nin çalıştırılmasıyla elde edilirse, konjonktif normal formdadır. Küme işlemleri açısından, Birlikler ile bağlantılı değişkenler arasında Kesişim ile elde edilen bileşik bir ifadedir.
Examples
$(A \lor B) \land (A \lor C) \land (B \lor C \lor D)$
$(P \cup Q) \cap (Q \cup R)$
Ayrık Normal Form
VE'lerle bağlantılı değişkenler arasında (değişkenlerin olumsuzlanması dahil) VEYA'nın çalıştırılmasıyla elde edilen bir bileşik ifade, ayrık normal formdadır. Küme işlemleri açısından, Kesişimler ile bağlantılı değişkenler arasından Union tarafından elde edilen bileşik bir ifadedir.
Examples
$(A \land B) \lor (A \land C) \lor (B \land C \land D)$
$(P \cap Q) \cup (Q \cap R)$
Predicate Logic değişkenler içeren önermeler olan yüklemlerle ilgilenir.
Dayanak Mantığı - Tanım
Bir yüklem, belirli bir alanda tanımlanan bir veya daha fazla değişkenin ifadesidir. Değişkenleri olan bir yüklem, değişkene bir değer atayarak veya değişkeni ölçerek bir önerme yapılabilir.
Aşağıda bazı yüklem örnekleri verilmiştir -
- E (x, y) "x = y" göstersin
- X (a, b, c) "a + b + c = 0" göstersin
- M (x, y) "x, y ile evli" olsun.
İyi Şekillendirilmiş Formül
İyi Oluşturulmuş Formül (wff), aşağıdakilerden herhangi birini içeren bir yüklemdir -
Tüm önerme sabitleri ve önerme değişkenleri wffs
Eğer x bir değişkense ve Y bir wff ise, $\forall x Y$ ve $\exists x Y$ ayrıca wff
Gerçek değer ve yanlış değerler wffs
Her atomik formül bir wff
Wff'leri bağlayan tüm bağlantılar wff'lardır
Niceleyiciler
Öngörüler değişkeni, nicelik belirteçleri ile ölçülür. Yüklem mantığında iki tür niceleyici vardır - Evrensel Niceleyici ve Varoluşsal Niceleyici.
Evrensel Niceleyici
Evrensel niceleyici, kapsamı içindeki ifadelerin belirli değişkenin her değeri için doğru olduğunu belirtir. Sembolü ile gösterilir$\forall$.
$\forall x P(x)$ her x değerinde olduğu gibi okunur, P (x) doğrudur.
Example - "İnsan ölümlüdür" önerme biçimine dönüştürülebilir $\forall x P(x)$ burada P (x), x'in ölümlü olduğunu ve söylem evreninin tüm erkekler olduğunu gösteren yüklemdir.
Varoluşsal Niceleyici
Varoluşsal niceleyici, kapsamı içindeki ifadelerin belirli değişkenin bazı değerleri için doğru olduğunu belirtir. Sembolü ile gösterilir$\exists $.
$\exists x P(x)$ x'in bazı değerlerinde olduğu gibi okunur, P (x) doğrudur.
Example - "Bazı insanlar sahtekârdır" önerme biçimine dönüştürülebilir $\exists x P(x)$ burada P (x), x'in dürüst olmadığını ve söylem evreninin bazı insanlar olduğunu gösteren yüklemdir.
Yuvalanmış Niceleyiciler
Başka bir niceleyicinin kapsamında görünen bir nicelik belirteci kullanırsak, buna iç içe nicelik belirteci denir.
Example
$\forall\ a\: \exists b\: P (x, y)$ nerede $P (a, b)$ gösterir $a + b = 0$
$\forall\ a\: \forall\: b\: \forall\: c\: P (a, b, c)$ nerede $P (a, b)$ gösterir $a + (b + c) = (a + b) + c$
Note - $\forall\: a\: \exists b\: P (x, y) \ne \exists a\: \forall b\: P (x, y)$
Gerçeğini zaten bildiğimiz ifadelerden yeni ifadeler çıkarmak, Rules of Inference kullanılmış.
Çıkarım Kuralları ne içindir?
Matematiksel mantık genellikle mantıksal ispatlar için kullanılır. Kanıtlar, matematiksel ifadelerin doğruluk değerlerini belirleyen geçerli argümanlardır.
Bir argüman, bir dizi ifadedir. Son ifade, sonuçtur ve önceki tüm ifadeleri öncül (veya hipotez) olarak adlandırılır. Sembol "$\therefore$”, (Bu nedenle okuyun) sonucun önüne yerleştirilmiştir. Geçerli bir argüman, sonucun öncüllerin doğruluk değerlerinden çıktığı bir argümandır.
Çıkarım Kuralları, zaten sahip olduğumuz ifadelerden geçerli argümanlar oluşturmak için şablonlar veya yönergeler sağlar.
Çıkarım Kuralları Tablosu
| Çıkarım Kuralı | İsim | Çıkarım Kuralı | İsim |
|---|---|---|---|
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$ |
İlave |
$$\begin{matrix} P \lor Q \\ \lnot P \\ \hline \therefore Q \end{matrix}$$ |
Ayrık Hececilik |
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$ |
Bağlaç |
$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$ |
Varsayımsal Hececilik |
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$ |
Basitleştirme |
$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$ |
Yapıcı İkilem |
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$ |
Modus Ponens |
$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$ |
Yıkıcı İkilem |
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$ |
Modus Tollens |
İlave
P bir öncül ise, türetmek için Toplama kuralı kullanabiliriz $ P \lor Q $.
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$
Misal
P önermesi olsun, "Çok çalışıyor" doğru
Bu nedenle - "Ya çok çalışıyor ya da çok kötü bir öğrenci." Burada Q, “o çok kötü bir öğrenci” önermesidir.
Bağlaç
P ve Q iki öncül ise, birleşik kuralını türetmek için kullanabiliriz $ P \land Q $.
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$
Misal
Bırak P - "Çok çalışıyor"
Q - "O, sınıftaki en iyi çocuk"
Bu nedenle - "Çok çalışıyor ve sınıftaki en iyi çocuk"
Basitleştirme
Eğer $P \land Q$ bir önermedir, P'yi türetmek için Basitleştirme kuralını kullanabiliriz.
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$
Misal
"Çok çalışıyor ve sınıftaki en iyi çocuk", $P \land Q$
Bu nedenle - "Çok çalışıyor"
Modus Ponens
P ve $P \rightarrow Q$ iki öncül, Q türetmek için Modus Ponens kullanabiliriz.
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$
Misal
"Şifreniz varsa, facebook'a giriş yapabilirsiniz", $P \rightarrow Q$
"Şifreniz var", P
Bu nedenle - "Facebook'ta oturum açabilirsiniz"
Modus Tollens
Eğer $P \rightarrow Q$ ve $\lnot Q$ iki öncül, türetmek için Modus Tollens kullanabiliriz $\lnot P$.
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$
Misal
"Şifreniz varsa, facebook'a giriş yapabilirsiniz", $P \rightarrow Q$
"Facebook'a giriş yapamazsınız", $\lnot Q$
Bu nedenle - "Şifreniz yok"
Ayrık Hececilik
Eğer $\lnot P$ ve $P \lor Q$ iki öncül olduğundan, Q'yu türetmek için Ayırıcı Hececiliği kullanabiliriz.
$$\begin{matrix} \lnot P \\ P \lor Q \\ \hline \therefore Q \end{matrix}$$
Misal
"Dondurma vanilya aromalı değil", $\lnot P$
"Dondurma vanilya aromalıdır veya çikolata aromalıdır", $P \lor Q$
Bu nedenle - "Dondurma çikolata aromalıdır"
Varsayımsal Hececilik
Eğer $P \rightarrow Q$ ve $Q \rightarrow R$ iki öncül, varsayımsal Syllogism'i kullanarak $P \rightarrow R$
$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$
Misal
"Yağmur yağarsa okula gitmem", $P \rightarrow Q$
"Okula gitmezsem, ödev yapmama gerek kalmaz", $Q \rightarrow R$
Therefore − "If it rains, I won't need to do homework"
Constructive Dilemma
If $( P \rightarrow Q ) \land (R \rightarrow S)$ and $P \lor R$ are two premises, we can use constructive dilemma to derive $Q \lor S$.
$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$
Example
“If it rains, I will take a leave”, $( P \rightarrow Q )$
“If it is hot outside, I will go for a shower”, $(R \rightarrow S)$
“Either it will rain or it is hot outside”, $P \lor R$
Therefore − "I will take a leave or I will go for a shower"
Destructive Dilemma
If $(P \rightarrow Q) \land (R \rightarrow S)$ and $ \lnot Q \lor \lnot S $ are two premises, we can use destructive dilemma to derive $\lnot P \lor \lnot R$.
$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$
Example
“If it rains, I will take a leave”, $(P \rightarrow Q )$
“If it is hot outside, I will go for a shower”, $(R \rightarrow S)$
“Either I will not take a leave or I will not go for a shower”, $\lnot Q \lor \lnot S$
Therefore − "Either it does not rain or it is not hot outside"
Group Theory is a branch of mathematics and abstract algebra that defines an algebraic structure named as group. Generally, a group comprises of a set of elements and an operation over any two elements on that set to form a third element also in that set.
In 1854, Arthur Cayley, the British Mathematician, gave the modern definition of group for the first time −
“A set of symbols all of them different, and such that the product of any two of them (no matter in what order), or the product of any one of them into itself, belongs to the set, is said to be a group. These symbols are not in general convertible [commutative], but are associative.”
In this chapter, we will know about operators and postulates that form the basics of set theory, group theory and Boolean algebra.
Any set of elements in a mathematical system may be defined with a set of operators and a number of postulates.
A binary operator defined on a set of elements is a rule that assigns to each pair of elements a unique element from that set. For example, given the set $ A = \lbrace 1, 2, 3, 4, 5 \rbrace $, we can say $\otimes$ is a binary operator for the operation $c = a \otimes b$, if it specifies a rule for finding c for the pair of $(a,b)$, such that $a,b,c \in A$.
The postulates of a mathematical system form the basic assumptions from which rules can be deduced. The postulates are −
Closure
A set is closed with respect to a binary operator if for every pair of elements in the set, the operator finds a unique element from that set.
Example
Let $A = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
This set is closed under binary operator into $(\ast)$, because for the operation $c = a \ast b$, for any $a, b \in A$, the product $c \in A$.
The set is not closed under binary operator divide $(\div)$, because, for the operation $c = a \div b$, for any $a, b \in A$, the product c may not be in the set A. If $a = 7, b = 2$, then $c = 3.5$. Here $a,b \in A$ but $c \notin A$.
Associative Laws
A binary operator $\otimes$ on a set A is associative when it holds the following property −
$(x \otimes y) \otimes z = x \otimes (y \otimes z)$, where $x, y, z \in A $
Example
Let $A = \lbrace 1, 2, 3, 4 \rbrace$
The operator plus $( + )$ is associative because for any three elements, $x,y,z \in A$, the property $(x + y) + z = x + ( y + z )$ holds.
The operator minus $( - )$ is not associative since
$$( x - y ) - z \ne x - ( y - z )$$
Commutative Laws
A binary operator $\otimes$ on a set A is commutative when it holds the following property −
$x \otimes y = y \otimes x$, nerede $x, y \in A$
Misal
İzin Vermek $A = \lbrace 1, 2, 3, 4 \rbrace$
Operatör artı $( + )$ değişmeli çünkü herhangi iki öğe için $x,y \in A$, özellikler $x + y = y + x$ tutar.
Operatör eksi $( - )$ beri çağrışımlı değil
$$x - y \ne y - x$$
Dağıtım Kanunları
İki ikili operatör $\otimes$ ve $\circledast$ A kümesinde, operatöre dağıtılır $\circledast$ aşağıdaki mülk geçerli olduğunda -
$x \otimes (y \circledast z) = (x \otimes y) \circledast (x \otimes z)$, nerede $x, y, z \in A $
Misal
İzin Vermek $A = \lbrace 1, 2, 3, 4 \rbrace$
Operatörleri $( * )$ ve artı $( + )$ operatör + üzerinden dağıtılır çünkü herhangi üç öğe için $x,y,z \in A$, özellikler $x * ( y + z ) = ( x * y ) + ( x * z )$ tutar.
Ancak, bu operatörler dağıtım yapmaz $*$ dan beri
$$x + ( y * z ) \ne ( x + y ) * ( x + z )$$
Kimlik Öğesi
A kümesi, ikili işleme göre bir kimlik elemanına sahiptir. $\otimes$ A üzerinde, eğer bir eleman varsa $e \in A$, aşağıdaki mülk geçerli olacak şekilde -
$e \otimes x = x \otimes e$, nerede $x \in A$
Misal
İzin Vermek $Z = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$
Öğe 1, işlem açısından bir kimlik öğesidir $*$ çünkü herhangi bir unsur için $x \in Z$,
$$1 * x = x * 1$$
Öte yandan, eksi işlem için kimlik öğesi yoktur. $( - )$
Ters
Bir A kümesinin bir kimlik öğesi varsa $e$ ikili operatöre göre $\otimes $, her element için her zaman bir tersi olduğu söylenir $x \in A$başka bir unsur var $y \in A$, aşağıdaki mülk geçerli olacak şekilde -
$$x \otimes y = e$$
Misal
İzin Vermek $A = \lbrace \dots -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, \dots \rbrace$
Operasyon artı göz önüne alındığında $( + )$ ve $e = 0$, herhangi bir x elemanının tersi $(-x)$ dan beri $x + (x) = 0$
De Morgan Yasası
De Morgan Yasaları, tamamlayıcıları açısından iki (veya daha fazla) kümenin birleşimi ve kesişimi arasında bir çift dönüşüm verir. Kanunlar -
$$(A \cup B)' = A' \cap B'$$
$$(A \cap B)' = A' \cup B'$$
Misal
İzin Vermek $A = \lbrace 1, 2, 3, 4 \rbrace ,B = \lbrace 1, 3, 5, 7 \rbrace$, ve
Evrensel set $U = \lbrace 1, 2, 3, \dots, 9, 10 \rbrace$
$A' = \lbrace 5, 6, 7, 8, 9, 10 \rbrace$
$B' = \lbrace 2, 4, 6, 8, 9, 10 \rbrace$
$A \cup B = \lbrace 1, 2, 3, 4, 5, 7 \rbrace$
$A \cap B = \lbrace 1, 3 \rbrace $
$(A \cup B)' = \lbrace 6, 8, 9, 10 \rbrace$
$A' \cap B' = \lbrace 6, 8, 9, 10 \rbrace$
Böylece görüyoruz ki $(A \cup B)' = A' \cap B'$
$(A \cap B)' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
$A' \cup B' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$
Böylece görüyoruz ki $(A \cap B)' = A' \cup B'$
Yarıgrup
Sonlu veya sonsuz bir küme $‘S’$ ikili işlem ile $‘\omicron’$ (Kompozisyon), iki koşulu aynı anda tutuyorsa yarı grup olarak adlandırılır -
Closure - Her çift için $(a, b) \in S, \:(a \omicron b)$ sette bulunmalı $S$.
Associative - Her öğe için $a, b, c \in S, (a \omicron b) \omicron c = a \omicron (b \omicron c)$ tutmalıdır.
Misal
Toplama işlemi ile pozitif tamsayılar kümesi (sıfır hariç) bir yarı gruptur. Örneğin,$ S = \lbrace 1, 2, 3, \dots \rbrace $
Burada kapatma özelliği her çift için geçerli $(a, b) \in S, (a + b)$ S kümesinde mevcuttur. Örneğin, $1 + 2 = 3 \in S]$
İlişkili mülkiyet ayrıca her öğe için de geçerlidir $a, b, c \in S, (a + b) + c = a + (b + c)$. Örneğin,$(1 + 2) + 3 = 1 + (2 + 3) = 5$
Monoid
Monoid, kimlik öğesi olan bir yarı gruptur. Kimlik öğesi (ile gösterilir$e$ veya E) bir S kümesinin bir öğesidir, öyle ki $(a \omicron e) = a$her öğe için $a \in S$. Bir kimlik unsuru aynı zamandaunit element. Yani, bir monoid aynı anda üç özelliğe sahiptir -Closure, Associative, Identity element.
Misal
Çarpma işlemi ile pozitif tamsayılar kümesi (sıfır hariç) bir monoiddir. $S = \lbrace 1, 2, 3, \dots \rbrace $
Burada kapatma özelliği her çift için geçerli $(a, b) \in S, (a \times b)$ S kümesinde mevcuttur [Örneğin, $1 \times 2 = 2 \in S$ ve bunun gibi]
İlişkili mülkiyet ayrıca her öğe için de geçerlidir $a, b, c \in S, (a \times b) \times c = a \times (b \times c)$ [Örneğin, $(1 \times 2) \times 3 = 1 \times (2 \times 3) = 6$ ve bunun gibi]
Kimlik özelliği ayrıca her öğe için de geçerlidir $a \in S, (a \times e) = a$ [Örneğin, $(2 \times 1) = 2, (3 \times 1) = 3$ve bunun gibi]. Burada kimlik öğesi 1'dir.
Grup
Bir grup, ters elemanlı bir monoiddir. Bir S kümesinin ters elemanı (I ile gösterilir) öyle bir elemandır ki$(a \omicron I) = (I \omicron a) = a$, her öğe için $a \in S$. Bu nedenle, bir grup aynı anda dört özelliğe sahiptir - i) Kapanış, ii) İlişkilendirici, iii) Kimlik öğesi, iv) Ters öğe. Bir G grubunun sırası, G'deki elemanların sayısıdır ve bir gruptaki bir elemanın sırası, en az pozitif tamsayıdır n, öyle ki an, bu G grubunun kimlik elemanıdır.
Örnekler
Kümesi $N \times N$ tekil olmayan matrisler, matris çarpım işlemi altında bir grup oluşturur.
İkisinin ürünü $N \times N$ tekil olmayan matrisler de bir $N \times N$ kapanma özelliğini tutan tekil olmayan matris.
Matris çarpımının kendisi ilişkiseldir. Bu nedenle, ilişkisel mülkiyet hakları vardır.
Kümesi $N \times N$ tekil olmayan matrisler, kimlik öğesi özelliğini tutan kimlik matrisini içerir.
Tüm matrisler tekil olmadığından, hepsinin aynı zamanda tekil olmayan matrisler olan ters elemanları vardır. Dolayısıyla, ters mülkiyet de geçerlidir.
Abelian Grubu
Değişken grup G, eleman çiftinin olduğu bir gruptur. $(a,b) \in G$her zaman değişmeli yasaya sahiptir. Dolayısıyla, bir grup aynı anda beş özelliğe sahiptir - i) Kapanış, ii) İlişkisel, iii) Kimlik öğesi, iv) Ters öğe, v) Değişmeli.
Misal
Toplama işlemi ile pozitif tamsayılar kümesi (sıfır dahil) değişmeli bir gruptur. $G = \lbrace 0, 1, 2, 3, \dots \rbrace$
Burada kapatma özelliği her çift için geçerli $(a, b) \in S, (a + b)$ S kümesinde mevcuttur [Örneğin, $1 + 2 = 2 \in S$ ve bunun gibi]
İlişkili mülkiyet ayrıca her öğe için de geçerlidir $a, b, c \in S, (a + b) + c = a + (b + c)$ [Örneğin, $(1 +2) + 3 = 1 + (2 + 3) = 6$ ve bunun gibi]
Kimlik özelliği ayrıca her öğe için de geçerlidir $a \in S, (a \times e) = a$ [Örneğin, $(2 \times 1) = 2, (3 \times 1) = 3$ve bunun gibi]. Burada kimlik öğesi 1'dir.
Değişmeli özellik ayrıca her öğe için de geçerlidir $a \in S, (a \times b) = (b \times a)$ [Örneğin, $(2 \times 3) = (3 \times 2) = 3$ ve bunun gibi]
Döngüsel Grup ve Alt Grup
Bir cyclic grouptek bir eleman tarafından oluşturulabilen bir gruptur. Döngüsel bir grubun her elemanı, bir jeneratör adı verilen belirli bir elemanın gücüdür. Döngüsel bir grup, bir jeneratör 'g' tarafından üretilebilir, öyle ki grubun diğer her elemanı, jeneratör 'g' gücü olarak yazılabilir.
Misal
Karmaşık sayılar kümesi $\lbrace 1,-1, i, -i \rbrace$ çarpma işlemi altında döngüsel bir gruptur.
İki jeneratör var - $i$ ve $–i$ gibi $i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1$ ve ayrıca $(–i)^1 = -i, (–i)^2 = -1, (–i)^3 = i, (–i)^4 = 1$grubun tüm unsurlarını kapsar. Dolayısıyla, döngüsel bir gruptur.
Note - bir cyclic groupher zaman değişmeli bir gruptur, ancak her değişmeli grup bir döngüsel grup değildir. Toplanan rasyonel sayılar döngüsel değildir, değişkendir.
Bir subgroup H, G grubunun bir alt kümesidir ( $H ≤ G$) aynı anda dört özelliği karşılarsa - Closure, Associative, Identity element, ve Inverse.
G grubunun tamamını içermeyen bir G grubunun bir H alt grubuna uygun bir alt grup denir ( $H < G$). Bir siklik grubun bir alt grubu döngüseldir ve bir değişmeli alt grup da değişmeli.
Misal
Bir grup olsun $G = \lbrace 1, i, -1, -i \rbrace$
Sonra bazı alt gruplar $H_1 = \lbrace 1 \rbrace, H_2 = \lbrace 1,-1 \rbrace$,
Bu bir alt grup değil - $H_3 = \lbrace 1, i \rbrace$ cünkü bu $(i)^{-1} = -i$ içinde değil $H_3$
Kısmen Sipariş Edilmiş Set (POSET)
Kısmen sıralı bir küme, dönüşlü, antisimetrik ve geçişli bir ikili ilişkiye sahip bir kümeden oluşur. "Kısmen sıralı küme" POSET olarak kısaltılır.
Örnekler
İkili işlem altında gerçek sayılar kümesi küçük veya eşittir $(\le)$ bir poset.
Set edelim $S = \lbrace 1, 2, 3 \rbrace$ ve operasyon $\le$
İlişkiler olacak $\lbrace(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)\rbrace$
Bu R ilişkisi refleksiftir $\lbrace (1, 1), (2, 2), (3, 3)\rbrace \in R$
Bu R ilişkisi anti-simetriktir.
$\lbrace (1, 2), (1, 3), (2, 3) \rbrace \in R\ and\ \lbrace (1, 2), (1, 3), (2, 3) \rbrace ∉ R$
Bu ilişki R aynı zamanda geçişlidir $\lbrace (1,2), (2,3), (1,3)\rbrace \in R$.
Bu nedenle, bu bir poset.
'Ulaşılabilirlik' operasyonu altındaki yönlendirilmiş çevrimsiz grafiğin tepe noktası kümesi bir pozettir.
Hasse Diyagramı
Bir kümenin Hasse diyagramı, köşeleri bu kümenin öğesi olan ve yaylar kümedeki çiftleri (x, y) kapsayan yönlendirilmiş grafiktir. Eğer poset içinde ise$x < y$, sonra x noktası Hasse diyagramında y noktasından daha aşağıda görünür. Eğer$x<y<z$ poset içinde ok, örtük olduğu için x ve z arasında gösterilmez.
Misal
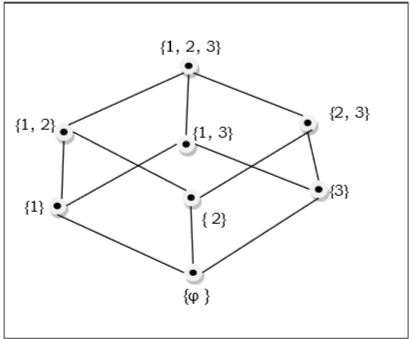
Alt kümelerinin poz kümesi $\lbrace 1, 2, 3 \rbrace = \lbrace \emptyset, \lbrace 1 \rbrace, \lbrace 2 \rbrace, \lbrace 3 \rbrace, \lbrace 1, 2 \rbrace, \lbrace 1, 3 \rbrace, \lbrace 2, 3 \rbrace, \lbrace 1, 2, 3 \rbrace \rbrace$ aşağıdaki Hasse diyagramı ile gösterilmiştir -
Doğrusal Sıralı Set
Doğrusal sıralı küme veya Toplam sıralı küme, her öğe çiftinin karşılaştırılabilir olduğu kısmi bir sıra kümesidir. Elementler$a, b \in S$ karşılaştırılabilir olduğu söyleniyor $a \le b$ veya $b \le a$tutar. Trikotomi yasası, bu toplam sıralı seti tanımlar. Tamamen sıralı bir küme, özelliğe sahip bir dağıtım kafes olarak tanımlanabilir$\lbrace a \lor b, a \land b \rbrace = \lbrace a, b \rbrace$ S kümesindeki tüm a ve b değerleri için
Misal
Güç kümesi $\lbrace a, b \rbrace$ \ subseteq tarafından sıralanan, güç kümesinin tüm öğeleri olarak tamamen sıralı bir kümedir $P = \lbrace \emptyset, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace a, b\rbrace \rbrace$ karşılaştırılabilir.
Toplam olmayan sipariş seti örneği
Bir set $S = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ x işlemi altında y'yi böler, toplam sıralı bir küme değildir.
Burada herkes için $(x, y) \in S, x | y$tutmalı ama 2 | 3, çünkü 2, 3'ü bölmez veya 3, 2'yi bölmez. Dolayısıyla, toplam sıralı bir küme değildir.
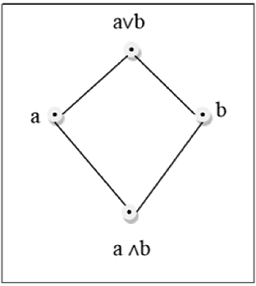
Kafes
Kafes bir posettir $(L, \le)$ her çift için $\lbrace a, b \rbrace \in L$ en az üst sınıra sahiptir (ile gösterilir $a \lor b$) ve en büyük alt sınır (ile gösterilir $a \land b$). YAĞLAMA$(\lbrace a,b \rbrace)$a ve b'nin birleşimi denir. GLB$(\lbrace a,b \rbrace )$ a ve b'nin buluşması denir.
Misal
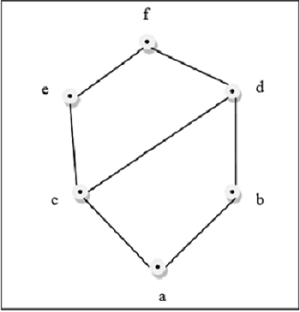
Yukarıdaki şekil bir kafestir çünkü her çift için $\lbrace a, b \rbrace \in L$, bir GLB ve bir LUB mevcuttur.
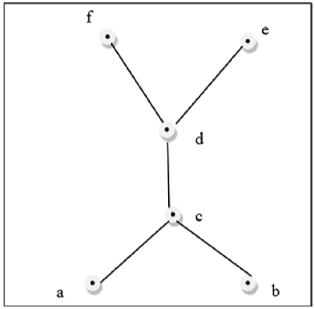
Yukarıdaki şekil bir kafes değildir çünkü $GLB (a, b)$ ve $LUB (e, f)$ mevcut değil.
Diğer bazı kafesler aşağıda tartışılmıştır -
Sınırlı Kafes
Bir L kafes, en büyük öğesi 1 ve en az öğesi 0 ise sınırlı bir kafes haline gelir.
Tamamlanmış Kafes
Bir kafes L, sınırlı bir kafes ise ve kafesteki her elemanın bir tamamlayıcısı varsa, tamamlanmış bir kafes haline gelir. Bir x elemanının x 'tamamlayıcısı vardır eğer$\exists x(x \land x’=0 and x \lor x’ = 1)$
Dağıtıcı Kafes
Bir kafes aşağıdaki iki dağılım özelliğini karşılarsa, buna bir dağıtım kafesi denir.
$a \lor (b \land c) = (a \lor b) \land (a \lor c)$
$a \land (b \lor c) = (a \land b) \lor (a \land c)$
Modüler Kafes
Bir kafes aşağıdaki özelliği karşılarsa, buna modüler kafes denir.
$a \land( b \lor (a \land d)) = (a \land b) \lor (a \land d)$
Kafeslerin Özellikleri
Idempotent Özellikleri
$a \lor a = a$
$a \land a = a$
Soğurma Özellikleri
$a \lor (a \land b) = a$
$a \land (a \lor b) = a$
Değişmeli Özellikler
$a \lor b = b \lor a$
$a \land b = b \land a$
İlişkili Özellikler
$a \lor (b \lor c) = (a \lor b) \lor c$
$a \land (b \land c) = (a \land b) \land c$
Bir Kafesin İkili
Bir kafesin ikilisi, '$\lor$' ve '$\land$' operasyonlar.
Misal
İkili $\lbrack a \lor (b \land c) \rbrack\ is\ \lbrack a \land (b \lor c) \rbrack$
Günlük yaşamda, çoğu kez, bir dizi olay için olası tüm sonuçların sayısını bulmak gerekir. Örneğin, 6 erkek ve 4 kadından oluşan bir yargıçlar kurulu 50 erkek ve 38 kadın arasından kaç şekilde seçilebilir? İlk beş harf büyük harf, sonraki dördü rakam ve sonuncusu yine büyük harf olacak şekilde kaç farklı 10 harfli PAN numarası üretilebilir. Bu problemleri çözmek için matematiksel sayma teorisi kullanılır.Counting esas olarak temel sayma kuralını, permütasyon kuralını ve kombinasyon kuralını kapsar.
Toplam ve Çarpım Kuralları
Rule of Sum ve Rule of Product zor sayma problemlerini basit problemlere ayırmak için kullanılır.
The Rule of Sum - Bir dizi görev varsa $T_1, T_2, \dots, T_m$ yapılabilir $w_1, w_2, \dots w_m$ sırasıyla yollar (koşul, hiçbir görevin aynı anda gerçekleştirilememesidir), bu durumda bu görevlerden birini yapmanın yollarının sayısı $w_1 + w_2 + \dots +w_m$. Ayrık olan iki görevi A ve B olarak ele alırsak (ör.$A \cap B = \emptyset$), sonra matematiksel olarak $|A \cup B| = |A| + |B|$
The Rule of Product - Bir dizi görev varsa $T_1, T_2, \dots, T_m$ yapılabilir $w_1, w_2, \dots w_m$ sırasıyla yollar ve her görev bir önceki görevin gerçekleşmesinden sonra gelirse, $w_1 \times w_2 \times \dots \times w_m$görevleri gerçekleştirmenin yolları. Matematiksel olarak, eğer bir B görevi bir A görevinden sonra gelirse, o zaman$|A \times B| = |A|\times|B|$
Misal
Question- X'te bir erkek çocuk yaşıyor ve Z'deki Okula gitmek istiyor. X'teki evinden önce Y'ye, sonra Y'den Z'ye varması gerekiyor. X'den Y'ye ya 3 otobüs güzergahı ya da 2 tren yolu ile gidebilir. Oradan Z'ye ulaşmak için 4 otobüs güzergahı veya 5 tren güzergahı seçebilir. X'den Z'ye gitmek için kaç yol vardır?
Solution - X'ten Y'ye, içeri girebilir $3 + 2 = 5$yollar (Toplam Kuralı). Daha sonra Y'den Z'ye gidebilir$4 + 5 = 9$yollar (Toplam Kuralı). Dolayısıyla X'den Z'ye girebilir$5 \times 9 = 45$ yollar (Ürün Kuralı).
Permütasyonlar
Bir permutationsıranın önemli olduğu bazı unsurların bir düzenlemesidir. Başka bir deyişle, bir Permütasyon, öğelerin sıralı bir Kombinasyonudur.
Örnekler
Bir seferde iki alarak S = {x, y, z} kümesinden tüm permütasyonlar -
$ xy, yx, xz, zx, yz, zy $.
Bir dizi sayıdan üç basamaklı bir sayının permütasyonunu oluşturmalıyız $S = \lbrace 1, 2, 3 \rbrace$. Basamakları düzenlediğimizde farklı üç basamaklı sayılar oluşacaktır. Permütasyon = 123, 132, 213, 231, 312, 321 olacaktır.
Permütasyon Sayısı
Bir seferde 'r' alınan 'n' farklı şeylerin permütasyonlarının sayısı ile gösterilir $n_{P_{r}}$
$$n_{P_{r}} = \frac{n!}{(n - r)!}$$
nerede $n! = 1.2.3. \dots (n - 1).n$
Proof - "N" farklı öğe olmasına izin verin.
İlk sırayı doldurmanın n sayıda yolu vardır. İlk sırayı doldurduktan sonra (n-1) eleman sayısı kalır. Dolayısıyla, ikinci sırayı doldurmanın (n-1) yolları vardır. Birinci ve ikinci sırayı doldurduktan sonra (n-2) eleman sayısı kalır. Dolayısıyla, üçüncü sırayı doldurmanın (n-2) yolları vardır. Şimdi r'inci yeri doldurmanın yollarının sayısını [n - (r – 1)] = n – r + 1 şeklinde genelleyebiliriz
Yani, toplam hayır. birinci sıradan ikinci sıraya kadar doldurmanın yolları -
$n_{ P_{ r } } = n (n-1) (n-2)..... (n-r + 1)$
$= [n(n-1)(n-2) ... (n-r + 1)] [(n-r)(n-r-1) \dots 3.2.1] / [(n-r)(n-r-1) \dots 3.2.1]$
Dolayısıyla
$n_{ P_{ r } } = n! / (n-r)!$
Bazı önemli permütasyon formülleri
N tane element varsa$a_1$ bir çeşit benzer $a_2$ başka türden benzer; $a_3$ üçüncü tür ve benzerleri ve $a_r$ olan $r^{th}$ nazik, nerede $(a_1 + a_2 + ... a_r) = n$.
O halde, bu n nesnenin permütasyon sayısı = $n! / [(a_1!(a_2!) \dots (a_r!)]$.
Bir seferde n eleman alan n farklı elemanın permütasyon sayısı = $n_{P_n} = n!$
X belirli şeyler her zaman belirli yerleri işgal ettiğinde, bir seferde r element alan n farklı elementin permütasyonlarının sayısı = $n-x_{p_{r-x}}$
The number of permutations of n dissimilar elements when r specified things always come together is − $r! (n−r+1)!$
The number of permutations of n dissimilar elements when r specified things never come together is − $n!–[r! (n−r+1)!]$
The number of circular permutations of n different elements taken x elements at time = $^np_{x}/x$
The number of circular permutations of n different things = $^np_{n}/n$
Some Problems
Problem 1 − From a bunch of 6 different cards, how many ways we can permute it?
Solution − As we are taking 6 cards at a time from a deck of 6 cards, the permutation will be $^6P_{6} = 6! = 720$
Problem 2 − In how many ways can the letters of the word 'READER' be arranged?
Solution − There are 6 letters word (2 E, 1 A, 1D and 2R.) in the word 'READER'.
The permutation will be $= 6! /\: [(2!) (1!)(1!)(2!)] = 180.$
Problem 3 − In how ways can the letters of the word 'ORANGE' be arranged so that the consonants occupy only the even positions?
Solution − There are 3 vowels and 3 consonants in the word 'ORANGE'. Number of ways of arranging the consonants among themselves $= ^3P_{3} = 3! = 6$. The remaining 3 vacant places will be filled up by 3 vowels in $^3P_{3} = 3! = 6$ ways. Hence, the total number of permutation is $6 \times 6 = 36$
Combinations
A combination is selection of some given elements in which order does not matter.
The number of all combinations of n things, taken r at a time is −
$$^nC_{ { r } } = \frac { n! } { r!(n-r)! }$$
Problem 1
Find the number of subsets of the set $\lbrace1, 2, 3, 4, 5, 6\rbrace$ having 3 elements.
Solution
The cardinality of the set is 6 and we have to choose 3 elements from the set. Here, the ordering does not matter. Hence, the number of subsets will be $^6C_{3} = 20$.
Problem 2
There are 6 men and 5 women in a room. In how many ways we can choose 3 men and 2 women from the room?
Solution
The number of ways to choose 3 men from 6 men is $^6C_{3}$ and the number of ways to choose 2 women from 5 women is $^5C_{2}$
Hence, the total number of ways is − $^6C_{3} \times ^5C_{2} = 20 \times 10 = 200$
Problem 3
How many ways can you choose 3 distinct groups of 3 students from total 9 students?
Solution
Let us number the groups as 1, 2 and 3
For choosing 3 students for 1st group, the number of ways − $^9C_{3}$
The number of ways for choosing 3 students for 2nd group after choosing 1st group − $^6C_{3}$
The number of ways for choosing 3 students for 3rd group after choosing 1st and 2nd group − $^3C_{3}$
Hence, the total number of ways $= ^9C_{3} \times ^6C_{3} \times ^3C_{3} = 84 \times 20 \times 1 = 1680$
Pascal's Identity
Pascal's identity, first derived by Blaise Pascal in 17th century, states that the number of ways to choose k elements from n elements is equal to the summation of number of ways to choose (k-1) elements from (n-1) elements and the number of ways to choose elements from n-1 elements.
Mathematically, for any positive integers k and n: $^nC_{k} = ^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$
Proof −
$$^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$$
$= \frac{ (n-1)! } { (k-1)!(n-k)! } + \frac{ (n-1)! } { k!(n-k-1)! }$
$= (n-1)!(\frac{ k } { k!(n-k)! } + \frac{ n-k } { k!(n-k)! } )$
$= (n-1)! \frac{ n } { k!(n-k)! }$
$= \frac{ n! } { k!(n-k)! }$
$= n_{ C_{ k } }$
Pigeonhole Principle
In 1834, German mathematician, Peter Gustav Lejeune Dirichlet, stated a principle which he called the drawer principle. Now, it is known as the pigeonhole principle.
Pigeonhole Principle states that if there are fewer pigeon holes than total number of pigeons and each pigeon is put in a pigeon hole, then there must be at least one pigeon hole with more than one pigeon. If n pigeons are put into m pigeonholes where n > m, there's a hole with more than one pigeon.
Examples
Ten men are in a room and they are taking part in handshakes. If each person shakes hands at least once and no man shakes the same man’s hand more than once then two men took part in the same number of handshakes.
There must be at least two people in a class of 30 whose names start with the same alphabet.
The Inclusion-Exclusion principle
The Inclusion-exclusion principle computes the cardinal number of the union of multiple non-disjoint sets. For two sets A and B, the principle states −
$|A \cup B| = |A| + |B| - |A \cap B|$
For three sets A, B and C, the principle states −
$|A \cup B \cup C | = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C |$
The generalized formula -
$|\bigcup_{i=1}^{n}A_i|=\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j|+\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k|- \dots +(-1)^{\pi-1}|A_1 \cap \dots \cap A_2|$
Problem 1
How many integers from 1 to 50 are multiples of 2 or 3 but not both?
Solution
From 1 to 100, there are $50/2 = 25$ numbers which are multiples of 2.
There are $50/3 = 16$ numbers which are multiples of 3.
There are $50/6 = 8$ numbers which are multiples of both 2 and 3.
So, $|A|=25$, $|B|=16$ and $|A \cap B|= 8$.
$|A \cup B| = |A| + |B| - |A \cap B| = 25 + 16 - 8 = 33$
Problem 2
In a group of 50 students 24 like cold drinks and 36 like hot drinks and each student likes at least one of the two drinks. How many like both coffee and tea?
Solution
Let X be the set of students who like cold drinks and Y be the set of people who like hot drinks.
So, $| X \cup Y | = 50$, $|X| = 24$, $|Y| = 36$
$|X \cap Y| = |X| + |Y| - |X \cup Y| = 24 + 36 - 50 = 60 - 50 = 10$
Hence, there are 10 students who like both tea and coffee.
Closely related to the concepts of counting is Probability. We often try to guess the results of games of chance, like card games, slot machines, and lotteries; i.e. we try to find the likelihood or probability that a particular result with be obtained.
Probability can be conceptualized as finding the chance of occurrence of an event. Mathematically, it is the study of random processes and their outcomes. The laws of probability have a wide applicability in a variety of fields like genetics, weather forecasting, opinion polls, stock markets etc.
Basic Concepts
Probability theory was invented in the 17th century by two French mathematicians, Blaise Pascal and Pierre de Fermat, who were dealing with mathematical problems regarding of chance.
Before proceeding to details of probability, let us get the concept of some definitions.
Random Experiment − An experiment in which all possible outcomes are known and the exact output cannot be predicted in advance is called a random experiment. Tossing a fair coin is an example of random experiment.
Sample Space − When we perform an experiment, then the set S of all possible outcomes is called the sample space. If we toss a coin, the sample space $S = \left \{ H, T \right \}$
Event − Any subset of a sample space is called an event. After tossing a coin, getting Head on the top is an event.
The word "probability" means the chance of occurrence of a particular event. The best we can say is how likely they are to happen, using the idea of probability.
$Probability\:of\:occurence\:of\:an\:event = \frac{Total\:number\:of\:favourable \: outcome}{Total\:number\:of\:Outcomes}$
As the occurrence of any event varies between 0% and 100%, the probability varies between 0 and 1.
Steps to find the probability
Step 1 − Calculate all possible outcomes of the experiment.
Step 2 − Calculate the number of favorable outcomes of the experiment.
Step 3 − Apply the corresponding probability formula.
Tossing a Coin
If a coin is tossed, there are two possible outcomes − Heads $(H)$ or Tails $(T)$
So, Total number of outcomes = 2
Hence, the probability of getting a Head $(H)$ on top is 1/2 and the probability of getting a Tails $(T)$ on top is 1/2
Throwing a Dice
When a dice is thrown, six possible outcomes can be on the top − $1, 2, 3, 4, 5, 6$.
The probability of any one of the numbers is 1/6
The probability of getting even numbers is 3/6 = 1/2
The probability of getting odd numbers is 3/6 = 1/2
Taking Cards From a Deck
From a deck of 52 cards, if one card is picked find the probability of an ace being drawn and also find the probability of a diamond being drawn.
Total number of possible outcomes − 52
Outcomes of being an ace − 4
Probability of being an ace = 4/52 = 1/13
Probability of being a diamond = 13/52 = 1/4
Probability Axioms
The probability of an event always varies from 0 to 1. $[0 \leq P(x) \leq 1]$
For an impossible event the probability is 0 and for a certain event the probability is 1.
If the occurrence of one event is not influenced by another event, they are called mutually exclusive or disjoint.
If $A_1, A_2....A_n$ are mutually exclusive/disjoint events, then $P(A_i \cap A_j) = \emptyset $ for $i \ne j$ and $P(A_1 \cup A_2 \cup.... A_n) = P(A_1) + P(A_2)+..... P(A_n)$
Properties of Probability
If there are two events $x$ and $\overline{x}$which are complementary, then the probability of the complementary event is −
$$p(\overline{x}) = 1-p(x)$$
For two non-disjoint events A and B, the probability of the union of two events −
$P(A \cup B) = P(A) + P(B)$
If an event A is a subset of another event B (i.e. $A \subset B$), then the probability of A is less than or equal to the probability of B. Hence, $A \subset B$ implies $P(A) \leq p(B)$
Conditional Probability
The conditional probability of an event B is the probability that the event will occur given an event A has already occurred. This is written as $P(B|A)$.
Mathematically − $ P(B|A) = P(A \cap B)/ P(A)$
If event A and B are mutually exclusive, then the conditional probability of event B after the event A will be the probability of event B that is $P(B)$.
Problem 1
In a country 50% of all teenagers own a cycle and 30% of all teenagers own a bike and cycle. What is the probability that a teenager owns bike given that the teenager owns a cycle?
Solution
Let us assume A is the event of teenagers owning only a cycle and B is the event of teenagers owning only a bike.
So, $P(A) = 50/100 = 0.5$ and $P(A \cap B) = 30/100 = 0.3$ from the given problem.
$P(B|A) = P(A \cap B)/ P(A) = 0.3/ 0.5 = 0.6$
Hence, the probability that a teenager owns bike given that the teenager owns a cycle is 60%.
Problem 2
In a class, 50% of all students play cricket and 25% of all students play cricket and volleyball. What is the probability that a student plays volleyball given that the student plays cricket?
Solution
Let us assume A is the event of students playing only cricket and B is the event of students playing only volleyball.
So, $P(A) = 50/100 =0.5$ and $P(A \cap B) = 25/ 100 =0.25$ from the given problem.
$P\lgroup B\rvert A \rgroup= P\lgroup A\cap B\rgroup/P\lgroup A \rgroup =0.25/0.5=0.5$
Hence, the probability that a student plays volleyball given that the student plays cricket is 50%.
Problem 3
Six good laptops and three defective laptops are mixed up. To find the defective laptops all of them are tested one-by-one at random. What is the probability to find both of the defective laptops in the first two pick?
Solution
Let A be the event that we find a defective laptop in the first test and B be the event that we find a defective laptop in the second test.
Hence, $P(A \cap B) = P(A)P(B|A) =3/9 \times 2/8 = 1/12$
Bayes' Theorem
Theorem − If A and B are two mutually exclusive events, where $P(A)$ is the probability of A and $P(B)$ is the probability of B, $P(A | B)$ is the probability of A given that B is true. $P(B | A)$ is the probability of B given that A is true, then Bayes’ Theorem states −
$$P(A|B) = \frac{P(B|A) P(A)}{\sum_{i = 1}^{n}P(B|Ai)P(Ai)}$$
Application of Bayes' Theorem
In situations where all the events of sample space are mutually exclusive events.
In situations where either $P( A_i \cap B )$ for each $A_i$ or $P( A_i )$ and $P(B|A_i)$ for each $A_i$ is known.
Problem
Consider three pen-stands. The first pen-stand contains 2 red pens and 3 blue pens; the second one has 3 red pens and 2 blue pens; and the third one has 4 red pens and 1 blue pen. There is equal probability of each pen-stand to be selected. If one pen is drawn at random, what is the probability that it is a red pen?
Solution
Let $A_i$ be the event that ith pen-stand is selected.
Here, i = 1,2,3.
Since probability for choosing a pen-stand is equal, $P(A_i) = 1/3$
Let B be the event that a red pen is drawn.
The probability that a red pen is chosen among the five pens of the first pen-stand,
$P(B|A_1) = 2/5$
The probability that a red pen is chosen among the five pens of the second pen-stand,
$P(B|A_2) = 3/5$
The probability that a red pen is chosen among the five pens of the third pen-stand,
$P(B|A_3) = 4/5$
According to Bayes' Theorem,
$P(B) = P(A_1).P(B|A_1) + P(A_2).P(B|A_2) + P(A_3).P(B|A_3)$
$= 1/3 . 2/5\: +\: 1/3 . 3/5\: +\: 1/3 . 4/5$
$= 3/5$
Mathematical induction, is a technique for proving results or establishing statements for natural numbers. This part illustrates the method through a variety of examples.
Definition
Mathematical Induction is a mathematical technique which is used to prove a statement, a formula or a theorem is true for every natural number.
The technique involves two steps to prove a statement, as stated below −
Step 1(Base step) − It proves that a statement is true for the initial value.
Step 2(Inductive step) − It proves that if the statement is true for the nth iteration (or number n), then it is also true for (n+1)th iteration ( or number n+1).
How to Do It
Step 1 − Consider an initial value for which the statement is true. It is to be shown that the statement is true for n = initial value.
Step 2 − Assume the statement is true for any value of n = k. Then prove the statement is true for n = k+1. We actually break n = k+1 into two parts, one part is n = k (which is already proved) and try to prove the other part.
Problem 1
$3^n-1$ is a multiple of 2 for n = 1, 2, ...
Solution
Step 1 − For $n = 1, 3^1-1 = 3-1 = 2$ which is a multiple of 2
Step 2 − Let us assume $3^n-1$ is true for $n=k$, Hence, $3^k -1$ is true (It is an assumption)
We have to prove that $3^{k+1}-1$ is also a multiple of 2
$3^{k+1} - 1 = 3 \times 3^k - 1 = (2 \times 3^k) + (3^k - 1)$
The first part $(2 \times 3k)$ is certain to be a multiple of 2 and the second part $(3k -1)$ is also true as our previous assumption.
Hence, $3^{k+1} – 1$ is a multiple of 2.
So, it is proved that $3^n – 1$ is a multiple of 2.
Problem 2
$1 + 3 + 5 + ... + (2n-1) = n^2$ for $n = 1, 2, \dots $
Solution
Step 1 − For $n=1, 1 = 1^2$, Hence, step 1 is satisfied.
Step 2 − Let us assume the statement is true for $n=k$.
Hence, $1 + 3 + 5 + \dots + (2k-1) = k^2$ is true (It is an assumption)
We have to prove that $1 + 3 + 5 + ... + (2(k+1)-1) = (k+1)^2$ also holds
$1 + 3 + 5 + \dots + (2(k+1) - 1)$
$= 1 + 3 + 5 + \dots + (2k+2 - 1)$
$= 1 + 3 + 5 + \dots + (2k + 1)$
$= 1 + 3 + 5 + \dots + (2k - 1) + (2k + 1)$
$= k^2 + (2k + 1)$
$= (k + 1)^2$
So, $1 + 3 + 5 + \dots + (2(k+1) - 1) = (k+1)^2$ hold which satisfies the step 2.
Hence, $1 + 3 + 5 + \dots + (2n - 1) = n^2$ is proved.
Problem 3
Prove that $(ab)^n = a^nb^n$ is true for every natural number $n$
Solution
Step 1 − For $n=1, (ab)^1 = a^1b^1 = ab$, Hence, step 1 is satisfied.
Step 2 − Let us assume the statement is true for $n=k$, Hence, $(ab)^k = a^kb^k$ is true (It is an assumption).
We have to prove that $(ab)^{k+1} = a^{k+1}b^{k+1}$ also hold
Given, $(ab)^k = a^k b^k$
Or, $(ab)^k (ab) = (a^k b^k ) (ab)$ [Multiplying both side by 'ab']
Or, $(ab)^{k+1} = (aa^k) ( bb^k)$
Or, $(ab)^{k+1} = (a^{k+1}b^{k+1})$
Hence, step 2 is proved.
So, $(ab)^n = a^nb^n$ is true for every natural number n.
Strong Induction
Strong Induction is another form of mathematical induction. Through this induction technique, we can prove that a propositional function, $P(n)$ is true for all positive integers, $n$, using the following steps −
Step 1(Base step) − It proves that the initial proposition $P(1)$ true.
Step 2(Inductive step) − It proves that the conditional statement $[P(1) \land P(2) \land P(3) \land \dots \land P(k)] → P(k + 1)$ is true for positive integers $k$.
In this chapter, we will discuss how recursive techniques can derive sequences and be used for solving counting problems. The procedure for finding the terms of a sequence in a recursive manner is called recurrence relation. We study the theory of linear recurrence relations and their solutions. Finally, we introduce generating functions for solving recurrence relations.
Definition
A recurrence relation is an equation that recursively defines a sequence where the next term is a function of the previous terms (Expressing $F_n$ as some combination of $F_i$ with $i < n$).
Example − Fibonacci series − $F_n = F_{n-1} + F_{n-2}$, Tower of Hanoi − $F_n = 2F_{n-1} + 1$
Linear Recurrence Relations
A linear recurrence equation of degree k or order k is a recurrence equation which is in the format $x_n= A_1 x_{n-1}+ A_2 x_{n-1}+ A_3 x_{n-1}+ \dots A_k x_{n-k} $($A_n$ is a constant and $A_k \neq 0$) on a sequence of numbers as a first-degree polynomial.
These are some examples of linear recurrence equations −
| Recurrence relations | Initial values | Solutions |
|---|---|---|
| Fn = Fn-1 + Fn-2 | a1 = a2 = 1 | Fibonacci number |
| Fn = Fn-1 + Fn-2 | a1 = 1, a2 = 3 | Lucas Number |
| Fn = Fn-2 + Fn-3 | a1 = a2 = a3 = 1 | Padovan sequence |
| Fn = 2Fn-1 + Fn-2 | a1 = 0, a2 = 1 | Pell number |
How to solve linear recurrence relation
Suppose, a two ordered linear recurrence relation is − $F_n = AF_{n-1} +BF_{n-2}$ where A and B are real numbers.
The characteristic equation for the above recurrence relation is −
$$x^2 - Ax - B = 0$$
Three cases may occur while finding the roots −
Case 1 − If this equation factors as $(x- x_1)(x- x_1) = 0$ and it produces two distinct real roots $x_1$ and $x_2$, then $F_n = ax_1^n+ bx_2^n$ is the solution. [Here, a and b are constants]
Case 2 − If this equation factors as $(x- x_1)^2 = 0$ and it produces single real root $x_1$, then $F_n = a x_1^n+ bn x_1^n$ is the solution.
Case 3 − If the equation produces two distinct complex roots, $x_1$ and $x_2$ in polar form $x_1 = r \angle \theta$ and $x_2 = r \angle(- \theta)$, then $F_n = r^n (a cos(n\theta)+ b sin(n\theta))$ is the solution.
Problem 1
Solve the recurrence relation $F_n = 5F_{n-1} - 6F_{n-2}$ where $F_0 = 1$ and $F_1 = 4$
Solution
The characteristic equation of the recurrence relation is −
$$x^2 - 5x + 6 = 0,$$
So, $(x - 3) (x - 2) = 0$
Hence, the roots are −
$x_1 = 3$ and $x_2 = 2$
The roots are real and distinct. So, this is in the form of case 1
Hence, the solution is −
$$F_n = ax_1^n + bx_2^n$$
Here, $F_n = a3^n + b2^n\ (As\ x_1 = 3\ and\ x_2 = 2)$
Therefore,
$1 = F_0 = a3^0 + b2^0 = a+b$
$4 = F_1 = a3^1 + b2^1 = 3a+2b$
Solving these two equations, we get $ a = 2$ and $b = -1$
Hence, the final solution is −
$$F_n = 2.3^n + (-1) . 2^n = 2.3^n - 2^n $$
Problem 2
Solve the recurrence relation − $F_n = 10F_{n-1} - 25F_{n-2}$ where $F_0 = 3$ and $F_1 = 17$
Solution
The characteristic equation of the recurrence relation is −
$$ x^2 - 10x -25 = 0$$
So $(x - 5)^2 = 0$
Hence, there is single real root $x_1 = 5$
As there is single real valued root, this is in the form of case 2
Hence, the solution is −
$F_n = ax_1^n + bnx_1^n$
$3 = F_0 = a.5^0 +(b)(0.5)^0 = a$
$17 = F_1 = a.5^1 + b.1.5^1 = 5a+5b$
Solving these two equations, we get $a = 3$ and $b = 2/5$
Hence, the final solution is − $F_n = 3.5^n +( 2/5) .n.2^n $
Problem 3
Solve the recurrence relation $F_n = 2F_{n-1} - 2F_{n-2}$ where $F_0 = 1$ and $F_1 = 3$
Solution
The characteristic equation of the recurrence relation is −
$$x^2 -2x -2 = 0$$
Hence, the roots are −
$x_1 = 1 + i$ and $x_2 = 1 - i$
In polar form,
$x_1 = r \angle \theta$ and $x_2 = r \angle(- \theta),$ where $r = \sqrt 2$ and $\theta = \frac{\pi}{4}$
The roots are imaginary. So, this is in the form of case 3.
Hence, the solution is −
$F_n = (\sqrt 2 )^n (a cos(n .\sqcap /4) + b sin(n .\sqcap /4))$
$1 = F_0 = (\sqrt 2 )^0 (a cos(0 .\sqcap /4) + b sin(0 .\sqcap /4) ) = a$
$3 = F_1 = (\sqrt 2 )^1 (a cos(1 .\sqcap /4) + b sin(1 . \sqcap /4) ) = \sqrt 2 ( a/ \sqrt 2 + b/ \sqrt 2)$
Solving these two equations we get $a = 1$ and $b = 2$
Hence, the final solution is −
$F_n = (\sqrt 2 )^n (cos(n .\pi /4 ) + 2 sin(n .\pi /4 ))$
Non-Homogeneous Recurrence Relation and Particular Solutions
A recurrence relation is called non-homogeneous if it is in the form
$F_n = AF_{n-1} + BF_{n-2} + f(n)$ where $f(n) \ne 0$
Its associated homogeneous recurrence relation is $F_n = AF_{n–1} + BF_{n-2}$
The solution $(a_n)$ of a non-homogeneous recurrence relation has two parts.
First part is the solution $(a_h)$ of the associated homogeneous recurrence relation and the second part is the particular solution $(a_t)$.
$$a_n=a_h+a_t$$
Solution to the first part is done using the procedures discussed in the previous section.
To find the particular solution, we find an appropriate trial solution.
Let $f(n) = cx^n$ ; let $x^2 = Ax + B$ be the characteristic equation of the associated homogeneous recurrence relation and let $x_1$ and $x_2$ be its roots.
If $x \ne x_1$ and $x \ne x_2$, then $a_t = Ax^n$
If $x = x_1$, $x \ne x_2$, then $a_t = Anx^n$
If $x = x_1 = x_2$, then $a_t = An^2x^n$
Example
Let a non-homogeneous recurrence relation be $F_n = AF_{n–1} + BF_{n-2} + f(n)$ with characteristic roots $x_1 = 2$ and $x_2 = 5$. Trial solutions for different possible values of $f(n)$ are as follows −