Ayrık Matematik - Grafikler Hakkında Daha Fazla Bilgi
Grafik Renklendirme
Grafik renklendirme, bitişik köşelerden hiçbirinin aynı rengi almaması için bir G grafiğinin her bir köşesine renk atama prosedürüdür. Amaç, bir grafiği renklendirirken renk sayısını en aza indirmektir. Bir G grafiğini renklendirmek için gereken en küçük renk sayısına, o grafiğin kromatik sayısı denir. Grafik renklendirme problemi bir NP Complete problemidir.
Bir Grafiği Renklendirme Yöntemi
Bir G grafiğini n sayıda köşeyle renklendirmek için gereken adımlar aşağıdaki gibidir -
Step 1 - Grafiğin köşelerini bir sırayla düzenleyin.
Step 2 - İlk tepe noktasını seçin ve onu ilk renkle renklendirin.
Step 3- Bir sonraki tepe noktasını seçin ve ona bitişik herhangi bir tepe noktasında renklendirilmemiş en düşük numaralı renkle renklendirin. Tüm bitişik köşeler bu renkle renklendirilmişse, ona yeni bir renk atayın. Tüm köşeler renklenene kadar bu adımı tekrarlayın.
Example
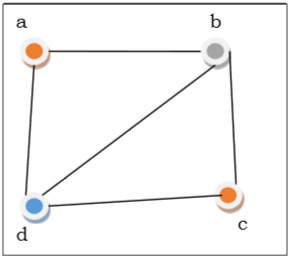
Yukarıdaki şekilde, ilk tepe noktasında $ a $ kırmızı renktedir. Köşe a'nın bitişik köşeleri yine bitişik olduğundan, köşe $ b $ ve köşe $ d $ sırasıyla farklı renk, yeşil ve mavi ile renklendirilir. Daha sonra, $ c $ 'ın komşu köşesi kırmızı renkte olmadığından, köşe $ c $ kırmızı renkte olur. Dolayısıyla grafiği 3 renge göre renklendirebiliriz. Dolayısıyla grafiğin kromatik sayısı 3'tür.
Grafik Renklendirme Uygulamaları
Bazı grafik renklendirme uygulamaları şunları içerir:
- Tahsis Kaydı
- Harita Boyama
- İki Taraflı Grafik Kontrolü
- Mobil Radyo Frekansı Ataması
- Zaman tablosu vb. Yapmak
Grafik Geçişi
Grafik geçişi, bir grafiğin tüm köşelerini sistematik bir sırayla ziyaret etme sorunudur. Bir grafikte gezinmenin başlıca iki yolu vardır.
- Kapsamlı İlk Arama
- Derinlik öncelikli arama
Kapsamlı İlk Arama
Kapsamlı İlk Arama (BFS), $ G $ grafiğinin 0. düzey tepe noktası $ X $ başlangıcında başlar. Sonra $ X $ 'ın komşuları olan tüm köşeleri ziyaret ediyoruz. Ziyaret ettikten sonra, köşeleri "ziyaret edilmiş" olarak işaretler ve 1. seviyeye yerleştiririz. Daha sonra 1. seviye köşelerden başlayıp aynı yöntemi 1. seviye köşe noktalarına vb. Uyguluyoruz. BFS geçişi, grafiğin her köşesi ziyaret edildiğinde sona erer.
BFS Algorithm
Konsept, komşu köşelerin diğer komşu köşelerini ziyaret etmeden önce tüm komşu köşeleri ziyaret etmektir.
Tüm düğümlerin durumunu "Hazır" olarak başlatın.
Kaynak köşe noktasını bir sıraya koyun ve durumunu "Bekliyor" olarak değiştirin.
Sıra boşalana kadar aşağıdaki iki adımı tekrarlayın -
Kuyruktan ilk tepe noktasını çıkarın ve "Ziyaret edildi" olarak işaretleyin.
Sıranın arkasına, durumu "Hazır" olan kaldırılan tepe noktasının tüm komşularını ekleyin. Durumlarını "Bekliyor" olarak işaretleyin.
Problem
Bir grafik alalım (Kaynak tepe noktası 'a'dır) ve geçiş sırasını bulmak için BFS algoritmasını uygulayalım.
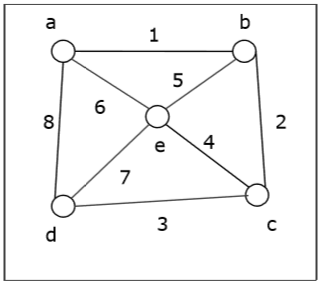
Solution -
Tüm köşelerin durumunu "Hazır" olarak başlatın.
Put bir kuyrukta ve “Waiting” duruma geçmeyecek.
Bir kuyruktan çıkarın , "Ziyaret edildi" olarak işaretleyin.
Ekle bir ‘hazır’ devlet içinde ‘ın komşuları b d ve e kuyruğunun bitirmek ve‘bekleme’olarak işaretlemek için.
Kaldır b kuyruğundan, “ziyaret etti” olarak işaretleyin, onun “hazır” komşu koymak c kuyrukta ve işareti sonunda c “bekleme” olarak.
Kaldır d kuyruktan ve “ziyaret etti” olarak işaretleyin. "Hazır" durumunda komşusu yoktur.
Kaldır e kuyruktan ve “ziyaret etti” olarak işaretleyin. "Hazır" durumunda komşusu yoktur.
Kaldır c kuyruktan ve “ziyaret etti” olarak işaretleyin. "Hazır" durumunda komşusu yoktur.
Sıra boş, bu yüzden durun.
Yani geçiş sırası -
$ a \ rightarrow b \ rightarrow d \ rightarrow e \ rightarrow c $
Alternatif geçiş sıraları şunlardır:
$ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $
Veya $ a \ rightarrow d \ rightarrow b \ rightarrow e \ rightarrow c $
Veya $ a \ rightarrow e \ rightarrow b \ rightarrow d \ rightarrow c $
Veya $ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $
Veya $ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $
Application of BFS
- En kısa yolu bulmak
- Ağırlıksız grafik için minimum kapsayan ağaç
- GPS navigasyon sistemi
- Yönlendirilmemiş bir grafikte döngüleri algılama
- Tek bir bağlı bileşen içindeki tüm düğümleri bulma
Complexity Analysis
$ G (V, E) $, $ | V | $ köşe sayısı ve $ | E | $ kenar sayısı olan bir grafik olsun. Genişlik ilk arama algoritması grafikteki her köşeyi ziyaret ederse ve her kenarı kontrol ederse, zaman karmaşıklığı -
$$ O (| V | + | E |). O (| E |) $$
$ O (1) $ ile $ O (| V2 |) $ arasında değişebilir
Derinlik öncelikli arama
Derinlik İlk Arama (DFS) algoritması bir köşe $ v $ 'dan başlar, daha sonra daha önce ziyaret edilmemiş olan bitişik köşesine (örneğin x) gider ve "ziyaret edilmiş" olarak işaretlenir ve $ x $' ın bitişiğindeki köşe ile devam eder ve yakında.
Herhangi bir tepe noktasında, tüm bitişik köşelerin ziyaret edildiğini görürse, daha önce geçilmemiş bitişik bir köşeye sahip olan ilk köşeyi bulana kadar geriye doğru izler. Daha sonra, bu tepe noktasından geçer, ziyaret edilen tüm köşeleri geçene kadar bitişik köşeleriyle devam eder ve tekrar geri gitmek zorunda kalır. Bu şekilde, ilk tepe noktasından $ v $ ulaşılabilen tüm köşeleri geçecektir.
DFS Algorithm
Kavram, diğer komşu köşeleri ziyaret etmeden önce bir komşu köşenin tüm komşu köşelerini ziyaret etmektir.
Tüm düğümlerin durumunu "Hazır" olarak başlatın
Kaynak köşe noktasını bir yığına koyun ve durumunu "Bekliyor" olarak değiştirin
Yığın boşalana kadar aşağıdaki iki adımı tekrarlayın -
Yığının üst köşesini açın ve "Ziyaret edildi" olarak işaretleyin
Durumu "Hazır" olan çıkarılan tepe noktasının tüm komşularını yığının üstüne itin. Durumlarını "Bekliyor" olarak işaretleyin.
Problem
Bir grafik alalım (Kaynak tepe noktası 'a'dır) ve geçiş sırasını bulmak için DFS algoritmasını uygulayalım.
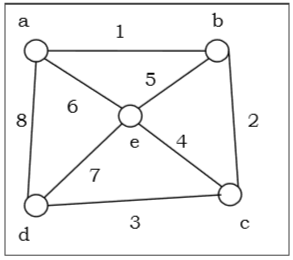
Solution
Tüm köşelerin durumunu "Hazır" olarak başlatın.
İtin bir yığınında ve “Waiting” duruma geçmeyecek.
Pop bir ve “ziyaret etti” olarak işaretleyin.
İtin bir ‘hazır’ devlet içinde bireyin komşuları e d ve b yığının üstüne ve ‘bekleme’ olarak işaretleyin.
Pop b yığından, onun “hazır” komşu itmek “ziyaret etti” olarak işaretleyin c stack'ına.
Pop c yığınından ve “ziyaret etti” olarak işaretlemek. "Hazır" komşusu yoktur.
Pop d yığınından ve “ziyaret etti” olarak işaretlemek. "Hazır" komşusu yoktur.
Pop e yığınından ve “ziyaret etti” olarak işaretlemek. "Hazır" komşusu yoktur.
Yığın boş. Bu yüzden dur.
Yani geçiş sırası -
$ a \ rightarrow b \ rightarrow c \ rightarrow d \ rightarrow e $
Alternatif geçiş sıraları şunlardır:
$ a \ rightarrow e \ rightarrow b \ rightarrow c \ rightarrow d $
Veya $ a \ rightarrow b \ rightarrow e \ rightarrow c \ rightarrow d $
Veya $ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $
Veya $ a \ rightarrow d \ rightarrow c \ rightarrow e \ rightarrow b $
Veya $ a \ rightarrow d \ rightarrow c \ rightarrow b \ rightarrow e $
Complexity Analysis
$ G (V, E) $, $ | V | $ köşe sayısı ve $ | E | $ kenar sayısı olan bir grafik olsun. DFS algoritması grafikteki her tepe noktasını ziyaret eder ve her kenarı kontrol ederse, zaman karmaşıklığı -
$$ \ circleddash (| V | + | E |) $$
Applications
- Döngüyü bir grafikte algılama
- Topolojik sıralamayı bulmak için
- Bir grafiğin iki taraflı olup olmadığını test etmek için
- Bağlı bileşenleri bulma
- Bir grafiğin köprülerini bulmak
- Grafiklerde ikili bağlantı bulma
- Knight's Tour problemini çözme
- Tek bir çözümle bulmacaları çözmek