Ağaçlara Giriş

Treetek tek öğeler veya düğümler arasındaki hiyerarşik ilişkileri temsil eden ayrı bir yapıdır. Bir ebeveynin ikiden fazla çocuğu olmadığı bir ağaca ikili ağaç denir.

Ağaç ve Özellikleri

Definition- Ağaç, bağlantılı, döngüsel olmayan, yönlendirilmemiş bir grafiktir. $ G $ 'daki her köşe çifti arasında benzersiz bir yol vardır. N sayıda köşeye sahip bir ağaç, $ (N-1) $ sayıda kenar içerir. 0 derecelik tepe noktasına ağacın kökü denir. 1 derecelik tepe noktası ağacın yaprak düğümü olarak adlandırılır ve bir iç düğümün derecesi en az 2'dir.

Example - Aşağıdaki bir ağaç örneğidir -

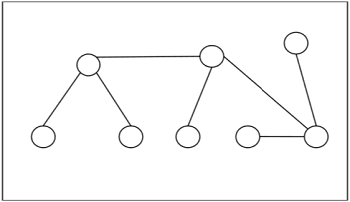
Bir Ağacın Merkezleri ve Bi-Merkezleri

Bir ağacın merkezi, minimum eksantrikliğe sahip bir tepe noktasıdır. Bir $ G $ ağacındaki bir $ X $ tepe noktasının eksantrikliği, $ X $ tepe noktası ile ağacın diğer herhangi bir tepe noktası arasındaki maksimum mesafedir. Maksimum eksantriklik ağaç çapıdır. Bir ağacın sadece bir merkezi varsa, buna Merkez Ağaç, bir ağacın birden fazla merkezi varsa, buna Bi-Merkez Ağaç denir. Her ağaç ya merkezi ya da iki merkezlidir.

Bir ağacın merkezlerini ve iki merkezlerini bulmaya yönelik algoritma

Step 1 - Verilen ağaçtan derece 1'in tüm köşelerini kaldırın ve ayrıca olay kenarlarını kaldırın.

Step 2- Tek bir tepe noktası veya bir kenarla birleştirilen iki köşe kalana kadar 1. adımı tekrarlayın. Tek bir tepe bırakılırsa, o zaman ağacın merkezidir ve bir kenarla birleştirilen iki köşe bırakılırsa, o zaman ağacın iki merkezidir.

Problem 1

Aşağıdaki ağacın ortasını / iki merkezini bulun -

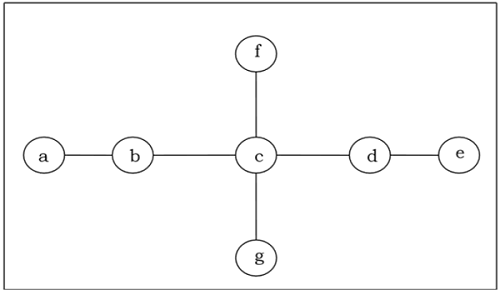
Solution

İlk önce, 1. derecenin tüm köşelerini kaldıracağız ve ayrıca olay kenarlarını kaldıracağız ve aşağıdaki ağacı alacağız -

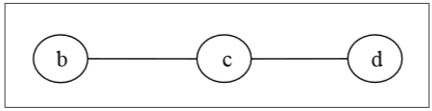
Yine, 1. derecenin tüm köşelerini kaldıracağız ve ayrıca olay kenarlarını kaldıracağız ve aşağıdaki ağacı alacağız -

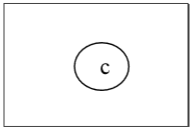
Sonunda tek bir köşe 'c' elde ettik ve algoritmayı durdurduk. Tek tepe noktası olduğundan, bu ağacın bir merkezi 'c' vardır ve ağaç merkezi bir ağaçtır.

Problem 2

Aşağıdaki ağacın ortasını / iki merkezini bulun -

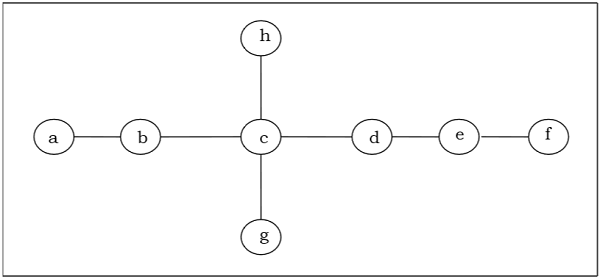
Solution

İlk önce, 1. derecenin tüm köşelerini kaldıracağız ve ayrıca olay kenarlarını kaldıracağız ve aşağıdaki ağacı alacağız -

Yine, 1. derecenin tüm köşelerini kaldıracağız ve ayrıca olay kenarlarını kaldıracağız ve aşağıdaki ağacı alacağız -

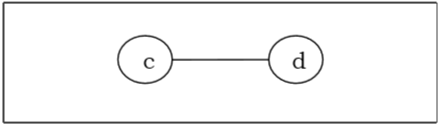
Son olarak, 'c' ve 'd' olmak üzere iki köşemiz kaldı, dolayısıyla algoritmayı durduruyoruz. Bir kenarla birleştirilmiş iki köşe kaldığı için, bu ağaç iki merkezli 'cd'ye sahiptir ve ağaç iki merkezlidir.

Etiketli Ağaçlar

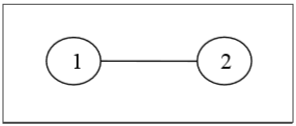
Definition- Etiketli ağaç, köşelerine 1'den n'ye kadar benzersiz sayılar atanan bir ağaçtır. Genel bir formül varsaymak için bu tür ağaçları küçük n değerleri için elle sayabiliriz. N sayıda köşenin etiketli ağaç sayısı $ n ^ {n-2} $ 'dır. Etiketli iki ağaç, grafikleri izomorfikse ve iki ağacın karşılık gelen noktaları aynı etiketlere sahipse izomorfiktir.

Misal

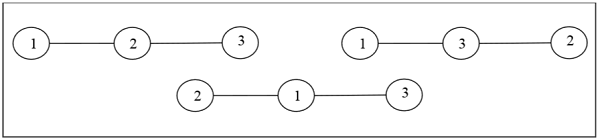
Etiketsiz Ağaçlar

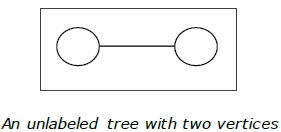
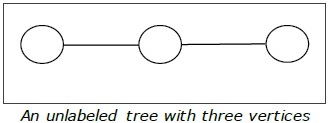
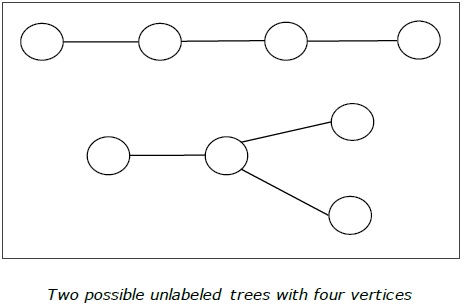
Definition- Etiketsiz ağaç, köşelerine herhangi bir numara atanmamış bir ağaçtır. N sayıda köşenin etiketli ağaç sayısı $ \ frac {(2n)!} {(N + 1)! N! } $ (n ^inci Katalan sayısı)

Misal

Köklü Ağaç

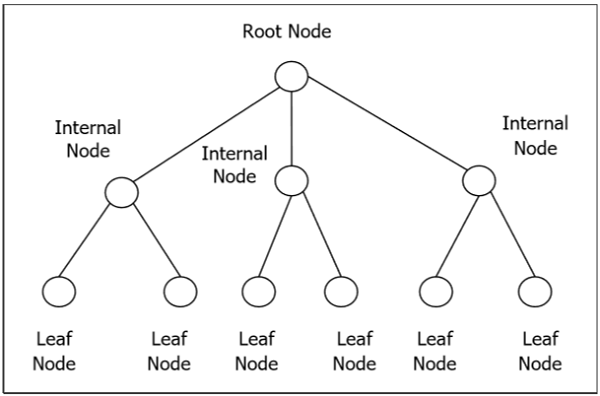
Köklü bir ağaç $ G $, ağacın kökü olarak adlandırılan ve her kenar doğrudan veya dolaylı olarak kökten kaynaklanan özel bir düğüme sahip, çevrimsiz bir grafiktir. Sıralı bir köklü ağaç, her iç tepe noktasının çocuklarının sıralandığı köklü bir ağaçtır. Köklü bir ağacın her iç tepe noktasında m'den fazla çocuk yoksa, buna m-ary ağacı denir. Köklü bir ağacın her iç tepe noktasının tam olarak m çocuğu varsa, buna tam m-ary ağaç denir. $ M = 2 $ ise, köklü ağaca ikili ağaç denir.

İkili Arama Ağacı

İkili Arama ağacı, aşağıdaki özelliği sağlayan bir ikili ağaçtır -

$ V köşenin sol alt ağacında $ X $, Değer (X) \ le Değer (V) $
$ V köşesinin sağ alt ağacında $ Y $, Değer (Y) \ ge Değer (V) $

Dolayısıyla, bir dahili düğüm $ V $ 'ın sol alt ağacının tüm köşelerinin değeri $ V $' dan küçük veya ona eşit ve $ V $ dahili düğümünün sağ alt ağacının tüm köşelerinin değeri $ V $ 'dan büyük veya ona eşit. Kök düğümden en derin düğüme olan bağlantıların sayısı İkili Arama Ağacının yüksekliğidir.

Misal

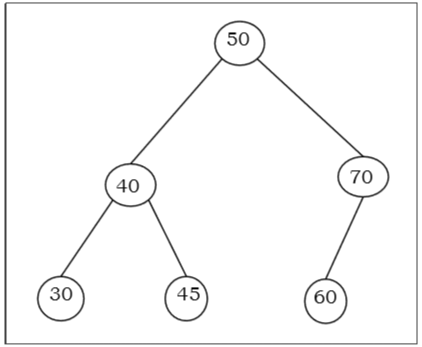
BST'de anahtar aramak için algoritma

BST_Search(x, k) 
if ( x = NIL or k = Value[x] ) 
   return x; 
if ( k < Value[x]) 
   return BST_Search (left[x], k); 
else  
   return BST_Search (right[x], k)

İkili arama ağacının karmaşıklığı

	Ortalama Vaka	En kötü durumda
Uzay Karmaşıklığı	O (n)	O (n)
Arama Karmaşıklığı	O (log n)	O (n)
Ekleme Karmaşıklığı	O (log n)	O (n)
Silme Karmaşıklığı	O (log n)	O (n)