Tối ưu hóa lồi - Hướng dẫn nhanh

Khóa học này hữu ích cho những sinh viên muốn giải quyết các vấn đề tối ưu hóa phi tuyến tính nảy sinh trong các ứng dụng kỹ thuật và khoa học khác nhau. Khóa học này bắt đầu với lý thuyết cơ bản của lập trình tuyến tính và sẽ giới thiệu các khái niệm về tập hợp lồi và hàm và các thuật ngữ liên quan để giải thích các định lý khác nhau được yêu cầu để giải quyết các vấn đề lập trình phi tuyến tính. Khóa học này sẽ giới thiệu các thuật toán khác nhau được sử dụng để giải quyết các vấn đề như vậy. Loại bài toán này nảy sinh trong các ứng dụng khác nhau bao gồm máy học, các bài toán tối ưu hóa trong kỹ thuật điện, v.v. Nó đòi hỏi học sinh phải có kiến ​​thức trước về các khái niệm và giải tích toán học phổ thông.

Trong khóa học này, sinh viên sẽ học cách giải các bài toán tối ưu hóa như $ min f \ left (x \ right) $ theo một số ràng buộc.

Những vấn đề này có thể giải quyết dễ dàng nếu hàm $ f \ left (x \ right) $ là một hàm tuyến tính và nếu các ràng buộc là tuyến tính. Khi đó nó được gọi là bài toán lập trình tuyến tính (LPP). Nhưng nếu các ràng buộc là phi tuyến tính thì khó có thể giải được bài toán trên. Trừ khi chúng ta có thể vẽ các hàm trong biểu đồ, thì việc cố gắng phân tích tối ưu hóa có thể là một cách, nhưng chúng ta không thể vẽ một hàm nếu nó vượt quá ba chiều. Do đó xuất hiện các kỹ thuật lập trình phi tuyến tính hoặc lập trình lồi để giải quyết các vấn đề như vậy. Trong hướng dẫn này, chúng tôi sẽ tập trung vào việc học các kỹ thuật như vậy và cuối cùng là một vài thuật toán để giải quyết các vấn đề như vậy. đầu tiên chúng ta sẽ đưa ra khái niệm về tập lồi là cơ sở của các bài toán lập trình lồi. Sau đó, với sự ra đời của các hàm lồi, chúng ta sẽ có một số định lý quan trọng để giải các bài toán này và một số thuật toán dựa trên các định lý này.

Thuật ngữ

• Không gian $ \ mathbb {R} ^ n $ - Nó là một vectơ n chiều với các số thực, được định nghĩa như sau - $ \ mathbb {R} ^ n = \ left \ {\ left (x_1, x_2, ... , x_n \ right) ^ {\ tau}: x_1, x_2, ...., x_n \ in \ mathbb {R} \ right \} $

• Không gian $ \ mathbb {R} ^ {mXn} $ - Nó là một tập hợp tất cả các ma trận giá trị thực có thứ tự $ mXn $.

Phương pháp luận

Lập trình tuyến tính còn được gọi là Tối ưu hóa tuyến tính, là một kỹ thuật được sử dụng để giải quyết các vấn đề toán học trong đó các mối quan hệ là tuyến tính. bản chất cơ bản của Lập trình tuyến tính là tối đa hóa hoặc giảm thiểuobjective function với chủ đề của một số constraints. Hàm mục tiêu là một hàm tuyến tính nhận được từ mô hình toán học của bài toán. Các ràng buộc là các điều kiện được áp dụng cho mô hình và cũng là tuyến tính.

• Từ câu hỏi đã cho, hãy tìm hàm mục tiêu.
• tìm các ràng buộc.
• Vẽ các ràng buộc trên đồ thị.
• tìm vùng khả thi, vùng này được hình thành bởi giao điểm của tất cả các ràng buộc.
• tìm các đỉnh của vùng khả thi.
• tìm giá trị của hàm mục tiêu tại các đỉnh này.
• Câu trả lời là cực đại hoặc cực tiểu của hàm mục tiêu (theo câu hỏi).

Ví dụ

Step 1 - Tối đa hóa $ 5x + 3y $ tùy theo

$ x + y \ leq 2 $,

$ 3x + y \ leq 3 $,

$ x \ geq 0 \: và \: y \ geq 0 $

Solution -

Bước đầu tiên là tìm vùng khả thi trên đồ thị.

Rõ ràng từ biểu đồ, các đỉnh của vùng khả thi là

$ \ left (0, 0 \ right) \ left (0, 2 \ right) \ left (1, 0 \ right) \ left (\ frac {1} {2}, \ frac {3} {2} \ right ) $

Cho $ f \ left (x, y \ right) = 5x + 3y $

Đặt các giá trị này vào hàm mục tiêu, chúng ta nhận được -

$ f \ left (0, 0 \ right) $ = 0

$ f \ left (0, 2 \ right) $ = 6

$ f \ left (1, 0 \ right) $ = 5

$ f \ left (\ frac {1} {2}, \ frac {3} {2} \ right) $ = 7

Do đó, hàm đạt cực đại tại $ \ left (\ frac {1} {2}, \ frac {3} {2} \ right) $

Step 2- Một công ty đồng hồ sản xuất đồng hồ kỹ thuật số và đồng hồ cơ. Các dự báo dài hạn cho thấy nhu cầu dự kiến ​​của ít nhất 100 đồng hồ kỹ thuật số và 80 đồng hồ cơ mỗi ngày. Do hạn chế về năng lực sản xuất, không quá 200 đồng hồ kỹ thuật số và 170 đồng hồ cơ có thể được sản xuất hàng ngày. Để đáp ứng hợp đồng vận chuyển, tổng cộng ít nhất 200 chiếc đồng hồ được vận chuyển mỗi ngày.

Nếu mỗi chiếc đồng hồ kỹ thuật số được bán dẫn đến lỗ $ \ $ 2 $, nhưng mỗi chiếc đồng hồ cơ khí lại tạo ra lợi nhuận $ \ $ 5 $, thì mỗi loại phải được sản xuất bao nhiêu chiếc hàng ngày để tối đa hóa lợi nhuận ròng?

Solution -

Gọi $ x $ là số lượng đồng hồ kỹ thuật số được sản xuất

$ y $ là số lượng đồng hồ cơ được sản xuất

Theo câu hỏi, ít nhất 100 đồng hồ kỹ thuật số sẽ được sản xuất hàng ngày và tối đa 200 đồng hồ kỹ thuật số có thể được sản xuất.

$ \ Rightarrow 100 \ leq \: x \ leq 200 $

Tương tự, ít nhất 80 đồng hồ cơ phải được sản xuất hàng ngày và tối đa 170 đồng hồ cơ có thể được sản xuất.

$ \ Rightarrow 80 \ leq \: y \ leq 170 $

Vì có ít nhất 200 chiếc đồng hồ được sản xuất mỗi ngày.

$ \ Mũi tên phải x + y \ leq 200 $

Vì mỗi chiếc đồng hồ kỹ thuật số bán ra dẫn đến lỗ $ \ $ 2 $, nhưng mỗi chiếc đồng hồ cơ khí lại tạo ra lợi nhuận $ \ $ 5 $,

Tổng lợi nhuận có thể được tính là

$ Lợi nhuận = -2x + 5y $

Và chúng tôi phải tối đa hóa lợi nhuận, Do đó, câu hỏi có thể được hình thành như:

Tối đa hóa $ -2x + 5y $ tùy theo

$ 100 \: \ leq x \: \ leq 200 $

$ 80 \: \ leq y \: \ leq 170 $

$ x + y \: \ leq 200 $

Vẽ các phương trình trên dưới dạng đồ thị, chúng ta nhận được,

Các đỉnh của vùng khả thi là

$ \ left (100, 170 \ right) \ left (200, 170 \ right) \ left (200, 180 \ right) \ left (120, 80 \ right) và \ left (100, 100 \ right) $

Giá trị lớn nhất của hàm mục tiêu nhận được là $ \ left (100, 170 \ right) $ Do đó, để tối đa hóa lợi nhuận ròng, nên sản xuất 100 đơn vị đồng hồ kỹ thuật số và 170 đơn vị đồng hồ cơ.

Chuẩn là một hàm cung cấp giá trị dương cho một vectơ hoặc một biến.

Định mức là một hàm $ f: \ mathbb {R} ^ n \ rightarrow \ mathbb {R} $

Các đặc điểm cơ bản của quy phạm là -

Gọi $ X $ là một vectơ sao cho $ X \ in \ mathbb {R} ^ n $

• $ \ left \ | x \ right \ | \ geq 0 $

• $ \ left \ | x \ right \ | = 0 \ Left rightarrow x = 0 \ forall x \ in X $

• $ \ left \ | \ alpha x \ right \ | = \ left | \ alpha \ right | \ left \ | x \ right \ | \ forall \: x \ in X và \: \ alpha \: is \: a \: vô hướng $

• $ \ left \ | x + y \ right \ | \ leq \ left \ | x \ right \ | + \ left \ | y \ right \ | \ forall x, y \ in X $

• $ \ left \ | xy \ right \ | \ geq \ left \ | \ left \ | x \ right \ | - \ left \ | y \ right \ | \ right \ | $

Theo định nghĩa, định mức được tính như sau:

• $ \ left \ | x \ right \ | _1 = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ left | x_i \ right | $

• $ \ left \ | x \ right \ | _2 = \ left (\ displaystyle \ sum \ limit_ {i = 1} ^ n \ left | x_i \ right | ^ 2 \ right) ^ {\ frac {1} {2}} $

• $ \ left \ | x \ right \ | _p = \ left (\ displaystyle \ sum \ limit_ {i = 1} ^ n \ left | x_i \ right | ^ p \ right) ^ {\ frac {1} {p}}, 1 \ leq p \ leq \ infty $

Định mức là một hàm liên tục.

Bằng chứng

Theo định nghĩa, nếu $ x_n \ rightarrow x $ trong $ X \ Rightarrow f \ left (x_n \ right) \ rightarrow f \ left (x \ right) $ thì $ f \ left (x \ right) $ là một hàm hằng.

Cho $ f \ left (x \ right) = \ left \ | x \ right \ | $

Do đó, $ \ left | f \ left (x_n \ right) -f \ left (x \ right) \ right | = \ left | \ left \ | x_n \ right \ | - \ trái \ | x \ right \ | \ right | \ leq \ left | \ trái | x_n-x \ right | \: \ right | $

Vì $ x_n \ rightarrow x $ nên $ \ left \ | x_n-x \ right \ | \ rightarrow 0 $

Do đó $ \ left | f \ left (x_n \ right) -f \ left (x \ right) \ right | \ leq 0 \ Rightarrow \ left | f \ left (x_n \ right) -f \ left (x \ right) \ right | = 0 \ Rightarrow f \ left (x_n \ right) \ rightarrow f \ left (x \ right) $

Do đó, định mức là một hàm liên tục.

Tích bên trong là một hàm cung cấp giá trị vô hướng cho một cặp vectơ.

Sản phẩm bên trong - $ f: \ mathbb {R} ^ n \ times \ mathbb {R} ^ n \ rightarrow \ kappa $ trong đó $ \ kappa $ là một đại lượng vô hướng.

Các đặc điểm cơ bản của sản phẩm bên trong như sau:

Cho $ X \ trong \ mathbb {R} ^ n $

• $ \ left \ langle x, x \ right \ rangle \ geq 0, \ forall x \ in X $

• $ \ left \ langle x, x \ right \ rangle = 0 \ Leftrightarrow x = 0, \ forall x \ in X $

• $ \ left \ langle \ alpha x, y \ right \ rangle = \ alpha \ left \ langle x, y \ right \ rangle, \ forall \ alpha \ in \ kappa \: và \: \ forall x, y \ in X $

• $ \ left \ langle x + y, z \ right \ rangle = \ left \ langle x, z \ right \ rangle + \ left \ langle y, z \ right \ rangle, \ forall x, y, z \ in X $

• $ \ left \ langle \ overline {y, x} \ right \ rangle = \ left (x, y \ right), \ forall x, y \ in X $

Note -

• Mối quan hệ giữa định mức và sản phẩm bên trong: $ \ left \ | x \ right \ | = \ sqrt {\ left (x, x \ right)} $

• $ \ forall x, y \ in \ mathbb {R} ^ n, \ left \ langle x, y \ right \ rangle = x_1y_1 + x_2y_2 + ... + x_ny_n $

Ví dụ

1. tìm tích bên trong của $ x = \ left (1,2,1 \ right) \: và \: y = \ left (3, -1,3 \ right) $

Giải pháp

$ \ left \ langle x, y \ right \ rangle = x_1y_1 + x_2y_2 + x_3y_3 $

$ \ left \ langle x, y \ right \ rangle = \ left (1 \ times3 \ right) + \ left (2 \ times-1 \ right) + \ left (1 \ times3 \ right) $

$ \ left \ langle x, y \ right \ rangle = 3 + \ left (-2 \ right) + 3 $

$ \ left \ langle x, y \ right \ rangle = 4 $

2. Nếu $ x = \ left (4,9,1 \ right), y = \ left (-3,5,1 \ right) $ và $ z = \ left (2,4,1 \ right) $, tìm $ \ left (x + y, z \ right) $

Giải pháp

Như chúng ta đã biết, $ \ left \ langle x + y, z \ right \ rangle = \ left \ langle x, z \ right \ rangle + \ left \ langle y, z \ right \ rangle $

$ \ left \ langle x + y, z \ right \ rangle = \ left (x_1z_1 + x_2z_2 + x_3z_3 \ right) + \ left (y_1z_1 + y_2z_2 + y_3z_3 \ right) $

$ \ left \ langle x + y, z \ right \ rangle = \ left \ {\ left (4 \ times 2 \ right) + \ left (9 \ times 4 \ right) + \ left (1 \ times1 \ right) \ right \} + $

$ \ left \ {\ left (-3 \ times2 \ right) + \ left (5 \ times4 \ right) + \ left (1 \ times 1 \ right) \ right \} $

$ \ left \ langle x + y, z \ right \ rangle = \ left (8 + 36 + 1 \ right) + \ left (-6 + 20 + 1 \ right) $

$ \ left \ langle x + y, z \ right \ rangle = 45 + 15 $

$ \ left \ langle x + y, z \ right \ rangle = 60 $

Thu nhỏ cục bộ hoặc Thu nhỏ

$ \ bar {x} \ in \: S $ được cho là cực tiểu cục bộ của hàm $ f $ if $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ trong đó $ N_ \ varepsilon \ left (\ bar {x} \ right) $ có nghĩa là vùng lân cận của $ \ bar {x} $, tức là $ N_ \ varepsilon \ left (\ bar {x} \ right) $ có nghĩa là $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $

Cực đại địa phương hoặc Bộ thu cực đại

$ \ bar {x} \ in \: S $ được cho là cực đại cục bộ của hàm $ f $ if $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ bar {x} \ right) $ trong đó $ N_ \ varepsilon \ left (\ bar {x} \ right) $ có nghĩa là vùng lân cận của $ \ bar {x} $, tức là $ N_ \ varepsilon \ left (\ bar {x} \ right) $ có nghĩa là $ \ left \ | x- \ bar {x} \ right \ | <\ varepsilon $

Cực tiểu toàn cầu

$ \ bar {x} \ in \: S $ được cho là cực tiểu toàn cục của một hàm $ f $ if $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ trong S $

Cực đại toàn cầu

$ \ bar {x} \ in \: S $ được cho là cực đại toàn cục của một hàm $ f $ if $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ forall x \ trong S $

Ví dụ

Step 1- tìm cực tiểu và cực đại cục bộ của $ f \ left (\ bar {x} \ right) = \ left | x ^ 2-4 \ phải | $

Solution -

Từ đồ thị của hàm trên, rõ ràng là cực tiểu cục bộ xảy ra tại $ x = \ pm 2 $ và cực đại cục bộ tại $ x = 0 $

Step 2- tìm cực tiểu toàn cục af của hàm $ f \ left (x \ right) = \ left | 4x ^ 3-3x ^ 2 + 7 \ right | $

Solution -

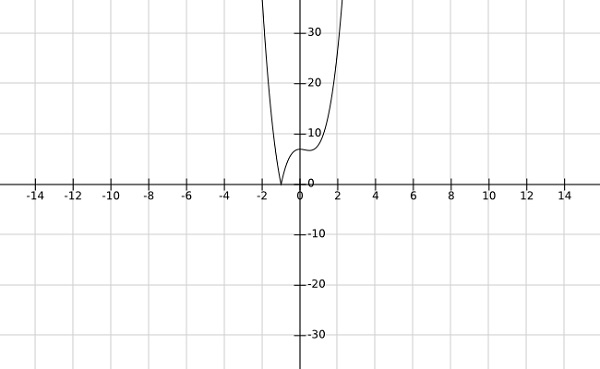
Từ đồ thị của hàm số trên, rõ ràng rằng cực tiểu toàn cục xảy ra tại $ x = -1 $.

Cho $ S \ subseteq \ mathbb {R} ^ n $ Một tập hợp S được cho là lồi nếu đoạn thẳng nối hai điểm bất kỳ của tập hợp S cũng thuộc S, tức là nếu $ x_1, x_2 \ in S $ rồi đến $ \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S $ trong đó $ \ lambda \ in \ left (0,1 \ right) $.

Note -

• Hợp của hai tập lồi có thể lồi hoặc không lồi.
• Giao của hai tập lồi luôn lồi.

Proof

Cho $ S_1 $ và $ S_2 $ là hai tập lồi.

Cho $ S_3 = S_1 \ cap S_2 $

Cho $ x_1, x_2 \ trong S_3 $

Vì $ S_3 = S_1 \ cap S_2 $ nên $ x_1, x_2 \ in S_1 $ và $ x_1, x_2 \ in S_2 $

Vì $ S_i $ là tập lồi nên $ \ forall $ $ i \ in 1,2, $

Do đó $ \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S_i $ trong đó $ \ lambda \ in \ left (0,1 \ right) $

Trước đó, $ \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ trong S_1 \ cap S_2 $

$ \ Rightarrow \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ trong S_3 $

Do đó, $ S_3 $ là một tập hợp lồi.

• Trung bình có trọng số của dạng $ \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i $, trong đó $ \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_i = 1 $ và $ \ lambda_i \ geq 0 , \ forall i \ in \ left [1, k \ right] $ được gọi là kết hợp conic của $ x_1, x_2, .... x_k. $

• Trung bình có trọng số của dạng $ \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i $, trong đó $ \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_i = 1 $ được gọi là kết hợp liên kết của $ x_1 , x_2, .... x_k. $

• Trung bình có trọng số của dạng $ \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i $ được gọi là kết hợp tuyến tính của $ x_1, x_2, .... x_k. $

Ví dụ

Step 1 - Chứng minh rằng tập hợp $ S = \ left \ {x \ in \ mathbb {R} ^ n: Cx \ leq \ alpha \ right \} $ là một tập hợp lồi.

Giải pháp

Cho $ x_1 $ và $ x_2 \ trong S $

$ \ Rightarrow Cx_1 \ leq \ alpha $ và $ \: và \: Cx_2 \ leq \ alpha $

Để hiển thị: $ \: \: y = \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ trong S \: \ forall \: \ lambda \ in \ left (0,1 \ đúng) $

$ Cy = C \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) = \ lambda Cx_1 + \ left (1- \ lambda \ right) Cx_2 $

$ \ Rightarrow Cy \ leq \ lambda \ alpha + \ left (1- \ lambda \ right) \ alpha $

$ \ Rightarrow Cy \ leq \ alpha $

$ \ Rightarrow y \ trong S $

Do đó, $ S $ là một tập lồi.

Step 2 - Chứng minh rằng tập hợp $ S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_ {1} ^ {2} \ leq 8x_2 \ right \} $ là một tập lồi bộ.

Giải pháp

Cho $ x, y \ trong S $

Cho $ x = \ left (x_1, x_2 \ right) $ và $ y = \ left (y_1, y_2 \ right) $

$ \ Rightarrow x_ {1} ^ {2} \ leq 8x_2 $ và $ y_ {1} ^ {2} \ leq 8y_2 $

Để hiển thị - $ \ lambda x + \ left (1- \ lambda \ right) y \ in S \ Rightarrow \ lambda \ left (x_1, x_2 \ right) + \ left (1- \ lambda \ right) \ left (y_1, y_2 \ right) \ trong S \ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda) y_2] \ trong S \ right) \ right] $

$ Now, \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} = \ lambda ^ 2x_ {1} ^ {2} + \ left (1- \ lambda \ right) ^ 2y_ {1} ^ {2} +2 \ lambda \ left (1- \ lambda \ right) x_1y_1 $

Nhưng $ 2x_1y_1 \ leq x_ {1} ^ {2} + y_ {1} ^ {2} $

Vì thế,

$ \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq \ lambda ^ 2x_ {1} ^ {2} + \ left (1- \ lambda \ right) ^ 2y_ {1} ^ {2} +2 \ lambda \ left (1- \ lambda \ right) \ left (x_ {1} ^ {2} + y_ {1} ^ {2} \ right) $

$ \ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq \ lambda x_ {1} ^ {2} + \ left (1- \ lambda \ right) y_ {1} ^ {2} $

$ \ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq 8 \ lambda x_2 + 8 \ left (1- \ lambda \ right) y_2 $

$ \ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda \ right) y_1 \ right] ^ {2} \ leq 8 \ left [\ lambda x_2 + \ left (1- \ lambda \ right) y_2 \ right] $

$ \ Rightarrow \ lambda x + \ left (1- \ lambda \ right) y \ trong S $

Step 3 - Chứng tỏ rằng một tập hợp $ S \ in \ mathbb {R} ^ n $ là lồi khi và chỉ khi với mỗi số nguyên k, mọi tổ hợp lồi của k điểm bất kỳ của $ S $ đều bằng $ S $.

Giải pháp

Cho $ S $ là một tập lồi. sau đó, để hiển thị;

$ c_1x_1 + c_2x_2 + ..... + c_kx_k \ in S, \ displaystyle \ sum \ limit_ {1} ^ k c_i = 1, c_i \ geq 0, \ forall i \ in 1,2, ...., k $

Chứng minh bằng quy nạp

Với $ k = 1, x_1 \ in S, c_1 = 1 \ Rightarrow c_1x_1 \ in S $

Với $ k = 2, x_1, x_2 \ in S, c_1 + c_2 = 1 $ và Vì S là một tập lồi

$ \ Rightarrow c_1x_1 + c_2x_2 \ in S. $

Gọi tổ hợp lồi của m điểm của S thuộc S tức là

$ c_1x_1 + c_2x_2 + ... + c_mx_m \ in S, \ displaystyle \ sum \ limit_ {1} ^ m c_i = 1, c_i \ geq 0, \ forall i \ in 1,2, ..., m $

Bây giờ, cho $ x_1, x_2 ...., x_m, x_ {m + 1} \ trong S $

Cho $ x = \ mu_1x_1 + \ mu_2x_2 + ... + \ mu_mx_m + \ mu_ {m + 1} x_ {m + 1} $

Cho $ x = \ left (\ mu_1 + \ mu_2 + ... + \ mu_m \ right) \ frac {\ mu_1x_1 + \ mu_2x_2 + \ mu_mx_m} {\ mu_1 + \ mu_2 + ......... + \ mu_m} + \ mu_ {m + 1} x_ {m + 1} $

Cho $ y = \ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_mx_m} {\ mu_1 + \ mu_2 + ......... + \ mu_m} $

$ \ Rightarrow x = \ left (\ mu_1 + \ mu_2 + ... + \ mu_m \ right) y + \ mu_ {m + 1} x_ {m + 1} $

Bây giờ $ y \ tính bằng S $ vì tổng các hệ số là 1.

$ \ Mũi tên phải x \ trong S $ vì S là tập lồi và $ y, x_ {m + 1} \ trong S $

Do đó được chứng minh bằng quy nạp.

Tập hợp $ A $ được cho là tập hợp liên kết nếu đối với bất kỳ hai điểm phân biệt nào, đường thẳng đi qua các điểm này nằm trong tập hợp $ A $.

Note -

• $ S $ là một tập hợp liên kết nếu và chỉ khi nó chứa mọi tổ hợp liên kết các điểm của nó.

• Tập rỗng và tập đơn đều là tập hợp affine và tập lồi.

  Ví dụ, nghiệm của một phương trình tuyến tính là một tập hợp affine.

Bằng chứng

Gọi S là nghiệm của một phương trình tuyến tính.

Theo định nghĩa, $ S = \ left \ {x \ in \ mathbb {R} ^ n: Ax = b \ right \} $

Cho $ x_1, x_2 \ trong S \ Rightarrow Ax_1 = b $ và $ Ax_2 = b $

Để chứng minh: $ A \ left [\ theta x_1 + \ left (1- \ theta \ right) x_2 \ right] = b, \ forall \ theta \ in \ left (0,1 \ right) $

$ A \ left [\ theta x_1 + \ left (1- \ theta \ right) x_2 \ right] = \ theta Ax_1 + \ left (1- \ theta \ right) Ax_2 = \ theta b + \ left (1- \ theta \ right ) b = b $

Do đó S là một tập hợp affine.

Định lý

Nếu $ C $ là một tập hợp liên kết và $ x_0 \ trong C $, thì tập hợp $ V = C-x_0 = \ left \ {x-x_0: x \ in C \ right \} $ là một không gian con của C.

Bằng chứng

Cho $ x_1, x_2 \ trong V $

Để hiển thị: $ \ alpha x_1 + \ beta x_2 \ in V $ cho một số $ \ alpha, \ beta $

Bây giờ, $ x_1 + x_0 \ trong C $ và $ x_2 + x_0 \ trong C $ theo định nghĩa của V

Bây giờ, $ \ alpha x_1 + \ beta x_2 + x_0 = \ alpha \ left (x_1 + x_0 \ right) + \ beta \ left (x_2 + x_0 \ right) + \ left (1- \ alpha - \ beta \ right) x_0 $

Nhưng $ \ alpha \ left (x_1 + x_0 \ right) + \ beta \ left (x_2 + x_0 \ right) + \ left (1- \ alpha - \ beta \ right) x_0 \ trong C $ vì C là một tập hợp liên kết .

Do đó, $ \ alpha x_1 + \ beta x_2 \ trong V $

Do đó đã chứng minh.

Phần lồi của một tập hợp các điểm trong S là biên của vùng lồi nhỏ nhất chứa tất cả các điểm của S bên trong nó hoặc trên biên của nó.

HOẶC LÀ

Cho $ S \ subseteq \ mathbb {R} ^ n $ Phần lồi của S, ký hiệu là $ Co \ left (S \ right) $ by là tập hợp tất cả các tổ hợp lồi của S, tức là $ x \ trong Co \ left (S \ right) $ nếu và chỉ khi $ x \ in \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_ix_i $, trong đó $ \ displaystyle \ sum \ limit_ {1} ^ n \ lambda_i = 1 $ và $ \ lambda_i \ geq 0 \ forall x_i \ bằng S $

Remark - Tập hợp các điểm thuộc S trong mặt phẳng xác định một đa giác lồi và các điểm của S trên biên của đa giác xác định các đỉnh của đa giác.

Theorem $ Co \ left (S \ right) = \ left \ {x: x = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_ix_i, x_i \ in S, \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_i = 1, \ lambda_i \ geq 0 \ right \} $ Chứng tỏ rằng một vỏ lồi là một tập lồi.

Bằng chứng

Đặt $ x_1, x_2 \ trong Co \ left (S \ right) $, sau đó $ x_1 = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_ix_i $ và $ x_2 = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_ \ gamma x_i $ trong đó $ \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_i = 1, \ lambda_i \ geq 0 $ và $ \ displaystyle \ sum \ limit_ {i = 1} ^ n \ gamma_i = 1, \ gamma_i \ geq0 $

Đối với $ \ theta \ in \ left (0,1 \ right), \ theta x_1 + \ left (1- \ theta \ right) x_2 = \ theta \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_ix_i + \ left (1- \ theta \ right) \ displaystyle \ sum \ limit_ {i = 1} ^ n \ gamma_ix_i $

$ \ theta x_1 + \ left (1- \ theta \ right) x_2 = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ lambda_i \ theta x_i + \ displaystyle \ sum \ limit_ {i = 1} ^ n \ gamma_i \ left (1- \ theta \ right) x_i $

$ \ theta x_1 + \ left (1- \ theta \ right) x_2 = \ displaystyle \ sum \ limit_ {i = 1} ^ n \ left [\ lambda_i \ theta + \ gamma_i \ left (1- \ theta \ right) \ phải] x_i $

Xem xét các hệ số,

$ \ displaystyle \ sum \ limit_ {i = 1} ^ n \ left [\ lambda_i \ theta + \ gamma_i \ left (1- \ theta \ right) \ right] = \ theta \ displaystyle \ sum \ limit_ {i = 1 } ^ n \ lambda_i + \ left (1- \ theta \ right) \ displaystyle \ sum \ limit_ {i = 1} ^ n \ gamma_i = \ theta + \ left (1- \ theta \ right) = 1 $

Do đó, $ \ theta x_1 + \ left (1- \ theta \ right) x_2 \ in Co \ left (S \ right) $

Do đó, một vỏ tàu lồi là một tập hợp lồi.

Gọi S là một tập tùy ý trong $ \ mathbb {R} ^ n $. Nếu $ x \ in Co \ left (S \ right) $, thì $ x \ in Co \ left (x_1, x_2, ...., x_n, x_ {n + 1} \ right) $.

Bằng chứng

Vì $ x \ in Co \ left (S \ right) $ nên $ x $ được biểu diễn bằng tổ hợp lồi của một số hữu hạn các điểm trong S, tức là

$ x = \ displaystyle \ sum \ limit_ {j = 1} ^ k \ lambda_jx_j, \ displaystyle \ sum \ limit_ {j = 1} ^ k \ lambda_j = 1, \ lambda_j \ geq 0 $ và $ x_j \ in S, \ forall j \ in \ left (1, k \ right) $

Nếu $ k \ leq n + 1 $, kết quả nhận được hiển nhiên là true.

Nếu $ k \ geq n + 1 $ thì $ \ left (x_2-x_1 \ right) \ left (x_3-x_1 \ right), ....., \ left (x_k-x_1 \ right) $ phụ thuộc tuyến tính .

$ \ Rightarrow \ tồn tại \ mu _j \ in \ mathbb {R}, 2 \ leq j \ leq k $ (không phải tất cả bằng 0) sao cho $ \ displaystyle \ sum \ limit_ {j = 2} ^ k \ mu _j \ left (x_j-x_1 \ right) = 0 $

Xác định $ \ mu_1 = - \ displaystyle \ sum \ limit_ {j = 2} ^ k \ mu _j $, rồi đến $ \ displaystyle \ sum \ limit_ {j = 1} ^ k \ mu_j x_j = 0, \ displaystyle \ sum \ giới hạn_ {j = 1} ^ k \ mu_j = 0 $

trong đó không phải tất cả $ \ mu_j's $ đều bằng 0. Vì $ \ displaystyle \ sum \ limit_ {j = 1} ^ k \ mu_j = 0 $, nên ít nhất một trong các $ \ mu_j> 0,1 \ leq j \ leq k $

Sau đó, $ x = \ displaystyle \ sum \ limit_ {1} ^ k \ lambda_j x_j + 0 $

$ x = \ displaystyle \ sum \ limit_ {1} ^ k \ lambda_j x_j- \ alpha \ displaystyle \ sum \ limit_ {1} ^ k \ mu_j x_j $

$ x = \ displaystyle \ sum \ limit_ {1} ^ k \ left (\ lambda_j- \ alpha \ mu_j \ right) x_j $

Chọn $ \ alpha $ sao cho $ \ alpha = min \ left \ {\ frac {\ lambda_j} {\ mu_j}, \ mu_j \ geq 0 \ right \} = \ frac {\ lambda_j} {\ mu _j}, $ cho một số $ i = 1,2, ..., k $

Nếu $ \ mu_j \ leq 0, \ lambda_j- \ alpha \ mu_j \ geq 0 $

Nếu $ \ mu_j> 0 thì \: \ frac {\ lambda _j} {\ mu_j} \ geq \ frac {\ lambda_i} {\ mu _i} = \ alpha \ Rightarrow \ lambda_j- \ alpha \ mu_j \ geq 0, j = 1,2, ... k $

Cụ thể, $ \ lambda_i- \ alpha \ mu_i = 0 $, theo định nghĩa của $ \ alpha $

$ x = \ displaystyle \ sum \ limit_ {j = 1} ^ k \ left (\ lambda_j- \ alpha \ mu_j \ right) x_j $, ở đâu

$ \ lambda_j- \ alpha \ mu_j \ geq0 $ và $ \ displaystyle \ sum \ limit_ {j = 1} ^ k \ left (\ lambda_j- \ alpha \ mu_j \ right) = 1 $ và $ \ lambda_i- \ alpha \ mu_i = 0 $

Do đó, x có thể được biểu diễn dưới dạng tổ hợp lồi của nhiều nhất (k-1) điểm.

Quá trình rút gọn này có thể được lặp lại cho đến khi x được biểu diễn dưới dạng tổ hợp lồi của (n + 1) phần tử.

Đặt S là một tập không rỗng, đóng và có giới hạn (còn được gọi là tập compact) trong $ \ mathbb {R} ^ n $ và đặt $ f: S \ rightarrow \ mathbb {R} $ là một hàm liên tục trên S, thì vấn đề tối thiểu $ \ left \ {f \ left (x \ right): x \ in S \ right \} $ đạt mức tối thiểu.

Bằng chứng

Vì S không rỗng và có giới hạn nên tồn tại một giới hạn dưới.

$ \ alpha = Inf \ left \ {f \ left (x \ right): x \ in S \ right \} $

Bây giờ hãy để $ S_j = \ left \ {x \ trong S: \ alpha \ leq f \ left (x \ right) \ leq \ alpha + \ delta ^ j \ right \} \ forall j = 1,2, ... $ và $ \ delta \ in \ left (0,1 \ right) $

Theo định nghĩa của infimium, $ S_j $ là không rỗng, cho mỗi $ j $.

Chọn một số $ x_j \ trong S_j $ để nhận một chuỗi $ \ left \ {x_j \ right \} $ với $ j = 1,2, ... $

Vì S bị giới hạn nên dãy cũng bị giới hạn và có một dãy con hội tụ $ \ left \ {y_j \ right \} $, hội tụ thành $ \ hat {x} $. Do đó $ \ hat {x} $ là điểm giới hạn và S bị đóng, do đó, $ \ hat {x} \ tính bằng S $. Vì f liên tục nên $ f \ left (y_i \ right) \ rightarrow f \ left (\ hat {x} \ right) $.

Vì $ \ alpha \ leq f \ left (y_i \ right) \ leq \ alpha + \ delta ^ k, \ alpha = \ displaystyle \ lim_ {k \ rightarrow \ infty} f \ left (y_i \ right) = f \ left ( \ hat {x} \ right) $

Do đó, $ \ hat {x} $ là giải pháp tối thiểu hóa.

Nhận xét

Có hai điều kiện cần thiết quan trọng để Định lý Weierstrass duy trì. Những điều này như sau:

• Step 1 - Tập hợp S nên là một tập có giới hạn.

  Xét hàm f \ left (x \ right) = x $.

  Nó là một tập hợp không bị ràng buộc và nó có cực tiểu tại bất kỳ điểm nào trong miền của nó.

  Do đó, để cực tiểu thu được, S phải có giới hạn.

• Step 2 - Tập hợp S nên đóng.

  Hãy xem xét hàm $ f \ left (x \ right) = \ frac {1} {x} $ trong miền \ left (0,1 \ right).

  Hàm này không được đóng trong miền đã cho và cực tiểu của nó cũng không tồn tại.

  Do đó, để thu được cực tiểu, S nên đóng.

Gọi S là một tập lồi đóng không rỗng trong $ \ mathbb {R} ^ n $ và đặt $ y \ notin S $, thì $ \ tồn tại $ a point $ \ bar {x} \ in S $ với khoảng cách nhỏ nhất từ y, tức là, $ \ left \ | y- \ bar {x} \ right \ | \ leq \ left \ | yx \ right \ | \ forall x \ in S. $

Hơn nữa, $ \ bar {x} $ là điểm thu nhỏ nếu và chỉ khi $ \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq 0 $ hoặc $ \ left (y- \ hat {x}, x- \ hat {x} \ right) \ leq 0 $

Bằng chứng

Sự tồn tại của điểm gần nhất

Vì $ S \ ne \ phi, \ tồn tại $ a point $ \ hat {x} \ trong S $ sao cho khoảng cách tối thiểu của S từ y nhỏ hơn hoặc bằng $ \ left \ | y- \ hat {x} \ right \ | $.

Xác định $ \ hat {S} = S \ cap \ left \ {x: \ left \ | yx \ right \ | \ leq \ left \ | y- \ hat {x} \ right \ | \ right \} $

Vì $ \ hat {S} $ là đóng và có giới hạn, và vì chuẩn là một hàm liên tục, nên theo định lý Weierstrass, tồn tại một điểm nhỏ nhất $ \ hat {x} \ trong S $ sao cho $ \ left \ | y- \ hat {x} \ right \ | = Inf \ left \ {\ left \ | yx \ right \ |, x \ trong S \ right \} $

Tính độc đáo

Giả sử $ \ bar {x} \ trong S $ sao cho $ \ left \ | y- \ hat {x} \ right \ | = \ left \ | y- \ hat {x} \ right \ | = \ alpha $

Vì S là lồi nên $ \ frac {\ hat {x} + \ bar {x}} {2} \ in S $

Nhưng, $ \ left \ | y- \ frac {\ hat {x} - \ bar {x}} {2} \ right \ | \ leq \ frac {1} {2} \ left \ | y- \ hat {x} \ right \ | + \ frac {1} {2} \ left \ | y- \ bar {x} \ right \ | = \ alpha $

Nó không thể là bất đẳng thức nghiêm ngặt vì $ \ hat {x} $ gần nhất với y.

Do đó, $ \ left \ | y- \ hat {x} \ right \ | = \ mu \ left \ | y- \ hat {x} \ right \ | $, với một số $ \ mu $

Bây giờ $ \ left \ | \ mu \ right \ | = 1. $ Nếu $ \ mu = -1 $ thì $ \ left (y- \ hat {x} \ right) = - \ left (y- \ hat {x} \ right) \ Rightarrow y = \ frac {\ hat {x} + \ bar {x}} {2} \ in S $

Nhưng $ y \ bằng S $. Do đó mâu thuẫn. Do đó $ \ mu = 1 \ Rightarrow \ hat {x} = \ bar {x} $

Do đó, điểm tối thiểu là duy nhất.

Đối với phần thứ hai của bằng chứng, giả sử $ \ left (y- \ hat {x} \ right) ^ {\ tau} \ left (x- \ bar {x} \ right) \ leq 0 $ cho tất cả $ x \ bằng S $

Hiện nay,

$ \ left \ | yx \ right \ | ^ {2} = \ left \ | y- \ hat {x} + \ hat {x} -x \ right \ | ^ {2} = \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ left \ | \ hat {x} -x \ right \ | ^ {2} +2 \ left (\ hat {x} -x \ right) ^ {\ tau} \ left (y- \ hat {x} \ right) $

$ \ Rightarrow \ left \ | yx \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ {2} $ vì $ \ left \ | \ hat {x} -x \ right \ | ^ {2} \ geq 0 $ và $ \ left (\ hat {x} - x \ right) ^ {T} \ left (y- \ hat {x} \ right ) \ geq 0 $

Do đó, $ \ hat {x} $ là điểm cực tiểu.

Ngược lại, giả sử $ \ hat {x} $ là điểm cực tiểu.

$ \ Rightarrow \ left \ | yx \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ 2 \ forall x \ in S $

Vì S là tập lồi.

$ \ Rightarrow \ lambda x + \ left (1- \ lambda \ right) \ hat {x} = \ hat {x} + \ lambda \ left (x- \ hat {x} \ right) \ in S $ với giá $ x \ in S $ và $ \ lambda \ in \ left (0,1 \ right) $

Bây giờ, $ \ left \ | y- \ hat {x} - \ lambda \ left (x- \ hat {x} \ right) \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ 2 $

Và

$ \ left \ | y- \ hat {x} - \ lambda \ left (x- \ hat {x} \ right) \ right \ | ^ {2} = \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ lambda ^ 2 \ left \ | x- \ hat {x} \ right \ | ^ {2} -2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) $

$ \ Rightarrow \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ lambda ^ {2} \ left \ | x- \ hat {x} \ right \ | -2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ geq \ left \ | y- \ hat {x} \ right \ | ^ {2} $

$ \ Rightarrow 2 \ lambda \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq \ lambda ^ 2 \ left \ | x- \ hat {x} \ right \ | ^ 2 $

$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ {T} \ left (x- \ hat {x} \ right) \ leq 0 $

Do đó đã được chứng minh.

Cho S là một tập lồi, đóng, không rỗng trong $ \ mathbb {R} ^ n $ và $ y \ notin S $. Sau đó, tồn tại một vectơ khác 0 $ p $ và vô hướng $ \ beta $ sao cho $ p ^ T y> \ beta $ và $ p ^ T x <\ beta $ cho mỗi $ x \ trong S $

Bằng chứng

Vì S là tập lồi đóng không rỗng và $ y \ notin S $ nên theo định lý điểm gần nhất, tồn tại một điểm cực tiểu duy nhất $ \ hat {x} \ trong S $ sao cho

$ \ left (x- \ hat {x} \ right) ^ T \ left (y- \ hat {x} \ right) \ leq 0 \ forall x \ in S $

Cho $ p = \ left (y- \ hat {x} \ right) \ neq 0 $ và $ \ beta = \ hat {x} ^ T \ left (y- \ hat {x} \ right) = p ^ T \ hat {x} $.

Sau đó $ \ left (x- \ hat {x} \ right) ^ T \ left (y- \ hat {x} \ right) \ leq 0 $

$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ T \ left (x- \ hat {x} \ right) \ leq 0 $

$ \ Rightarrow \ left (y- \ hat {x} \ right) ^ Tx \ leq \ left (y- \ hat {x} \ right) ^ T \ hat {x} = \ hat {x} ^ T \ left (y- \ hat {x} \ right) $ i, e., $ p ^ Tx \ leq \ beta $

Ngoài ra, $ p ^ Ty- \ beta = \ left (y- \ hat {x} \ right) ^ Ty- \ hat {x} ^ T \ left (y- \ hat {x} \ right) $

$ = \ left (y- \ hat {x} \ right) ^ T \ left (yx \ right) = \ left \ | y- \ hat {x} \ right \ | ^ {2}> 0 $

$ \ Rightarrow p ^ Ty> \ beta $

Định lý này dẫn đến việc phân tách các siêu mặt phẳng. Các siêu mặt phẳng dựa trên định lý trên có thể được định nghĩa như sau:

Gọi $ S_1 $ và $ S_2 $ là các tập con không rỗng của $ \ mathbb {R} $ và $ H = \ left \ {X: A ^ TX = b \ right \} $ là một siêu phẳng.

• Siêu phẳng H được cho là phân tách $ S_1 $ và $ S_2 $ nếu $ A ^ TX \ leq b \ forall X \ in S_1 $ và $ A_TX \ geq b \ forall X \ trong S_2 $

• Siêu phẳng H được cho là phân tách chặt chẽ $ S_1 $ và $ S_2 $ nếu $ A ^ TX <b \ forall X \ in S_1 $ và $ A_TX> b \ forall X \ trong S_2 $

• Siêu phẳng H được cho là phân tách rõ ràng $ S_1 $ và $ S_2 $ nếu $ A ^ TX \ leq b \ forall X \ in S_1 $ và $ A_TX \ geq b + \ varepsilon \ forall X \ in S_2 $, trong đó $ \ varepsilon $ là một đại lượng vô hướng dương.

Tập hợp C khác rỗng trong $ \ mathbb {R} ^ n $ được cho là hình nón với đỉnh 0 nếu $ x \ trong C \ Rightarrow \ lambda x \ trong C \ forall \ lambda \ geq 0 $.

Tập hợp C là một hình nón lồi nếu nó lồi cũng như hình nón.

Ví dụ: $ y = \ left | x \ right | $ không phải là hình nón lồi vì nó không lồi.

Nhưng, $ y \ geq \ left | x \ right | $ là một hình nón lồi vì nó lồi cũng như hình nón.

Note - Một hình nón C lồi khi và chỉ khi với bất kỳ $ x, y \ trong C, x + y \ trong C $.

Bằng chứng

Vì C là hình nón, cho $ x, y \ in C \ Rightarrow \ lambda x \ in C $ và $ \ mu y \ in C \: \ forall \: \ lambda, \ mu \ geq 0 $

C là lồi nếu $ \ lambda x + \ left (1- \ lambda \ right) y \ in C \: \ forall \: \ lambda \ in \ left (0, 1 \ right) $

Vì C là hình nón nên $ \ lambda x \ trong C $ và $ \ left (1- \ lambda \ right) y \ trong C \ Leftrightarrow x, y \ in C $

Do đó C là lồi nếu $ x + y \ in C $

Nói chung, nếu $ x_1, x_2 \ in C $, thì $ \ lambda_1x_1 + \ lambda_2x_2 \ in C, \ forall \ lambda_1, \ lambda_2 \ geq 0 $

Ví dụ

• Hợp số conic của tập vectơ vô hạn trong $ \ mathbb {R} ^ n $ là một hình nón lồi.

• Mọi tập hợp rỗng đều là một hình nón lồi.

• Bất kỳ hàm tuyến tính nào là một hình nón lồi.

• Vì một siêu phẳng là tuyến tính, nó cũng là một hình nón lồi.

• Các nửa không gian đóng cũng là hình nón lồi.

Note - Giao của hai hình nón lồi là một hình nón lồi nhưng hợp của chúng có thể là một hình nón lồi.

Gọi S là một tập khác rỗng trong $ \ mathbb {R} ^ n $ Khi đó, hình nón cực của S ký hiệu là $ S ^ * $ được cho bởi $ S ^ * = \ left \ {p \ in \ mathbb {R } ^ n, p ^ Tx \ leq 0 \: \ forall x \ in S \ right \} $.

Nhận xét

• Hình nón có cực luôn lồi ngay cả khi S không lồi.

• Nếu S là tập trống, $ S ^ * = \ mathbb {R} ^ n $.

• Sự phân cực có thể được coi là sự tổng quát của tính trực giao.

Đặt $ C \ subseteq \ mathbb {R} ^ n $ khi đó là không gian trực giao của C, ký hiệu là $ C ^ \ perp = \ left \ {y \ in \ mathbb {R} ^ n: \ left \ langle x, y \ right \ rangle = 0 \ forall x \ in C \ right \} $.

Bổ đề

Đặt $ S, S_1 $ và $ S_2 $ là các tập không rỗng trong $ \ mathbb {R} ^ n $ thì các câu sau là đúng:

• $ S ^ * $ là một hình nón lồi kín.

• $ S \ subseteq S ^ {**} $ trong đó $ S ^ {**} $ là một hình nón cực của $ S ^ * $.

• $ S_1 \ subseteq S_2 \ Rightarrow S_ {2} ^ {*} \ subseteq S_ {1} ^ {*} $.

Bằng chứng

Step 1 - $ S ^ * = \ left \ {p \ in \ mathbb {R} ^ n, p ^ Tx \ leq 0 \: \ forall \: x \ in S \ right \} $

• Cho $ x_1, x_2 \ in S ^ * \ Rightarrow x_ {1} ^ {T} x \ leq 0 $ và $ x_ {2} ^ {T} x \ leq 0, \ forall x \ in S $

  Đối với $ \ lambda \ in \ left (0, 1 \ right), \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right] ^ Tx = \ left [\ left (\ lambda x_1 \ right ) ^ T + \ left \ {\ left (1- \ lambda \ right) x_ {2} \ right \} ^ {T} \ right] x, \ forall x \ in S $

  $ = \ left [\ lambda x_ {1} ^ {T} + \ left (1- \ lambda \ right) x_ {2} ^ {T} \ right] x = \ lambda x_ {1} ^ {T} x + \ left (1- \ lambda \ right) x_ {2} ^ {T} \ leq 0 $

  Do đó $ \ lambda x_1 + \ left (1- \ lambda \ right) x_ {2} \ trong S ^ * $

  Do đó $ S ^ * $ là một tập lồi.

• Đối với $ \ lambda \ geq 0, p ^ {T} x \ leq 0, \ forall \: x \ in S $

  Do đó, $ \ lambda p ^ T x \ leq 0, $

  $ \ Rightarrow \ left (\ lambda p \ right) ^ T x \ leq 0 $

  $ \ Rightarrow \ lambda p \ trong S ^ * $

  Do đó, $ S ^ * $ là một hình nón.

• Để hiển thị $ S ^ * $ đã đóng, tức là để hiển thị nếu $ p_n \ rightarrow p $ dưới dạng $ n \ rightarrow \ infty $, thì $ p \ trong S ^ * $

  $ \ forall x \ in S, p_ {n} ^ {T} xp ^ T x = \ left (p_n-p \ right) ^ T x $

  Như $ p_n \ rightarrow p $ bằng $ n \ rightarrow \ infty \ Rightarrow \ left (p_n \ rightarrow p \ right) \ rightarrow 0 $

  Do đó $ p_ {n} ^ {T} x \ rightarrow p ^ {T} x $. Nhưng $ p_ {n} ^ {T} x \ leq 0, \: \ forall x \ trong S $

  Do đó, $ p ^ Tx \ leq 0, \ forall x \ in S $

  $ \ Rightarrow p \ trong S ^ * $

  Do đó, $ S ^ * $ đã bị đóng.

Step 2 - $ S ^ {**} = \ left \ {q \ in \ mathbb {R} ^ n: q ^ T p \ leq 0, \ forall p \ in S ^ * \ right \} $

Đặt $ x \ in S $, sau đó $ \ forall p \ in S ^ *, p ^ T x \ leq 0 \ Rightarrow x ^ Tp \ leq 0 \ Rightarrow x \ in S ^ {**} $

Do đó, $ S \ subseteq S ^ {**} $

Step 3 - $ S_2 ^ * = \ left \ {p \ in \ mathbb {R} ^ n: p ^ Tx \ leq 0, \ forall x \ in S_2 \ right \} $

Vì $ S_1 \ subseteq S_2 \ Rightarrow \ forall x \ in S_2 \ Rightarrow \ forall x \ in S_1 $

Do đó, nếu $ \ hat {p} \ in S_2 ^ *, $ thì $ \ hat {p} ^ Tx \ leq 0, \ forall x \ in S_2 $

$ \ Rightarrow \ hat {p} ^ Tx \ leq 0, \ forall x \ in S_1 $

$ \ Rightarrow \ hat {p} ^ T \ trong S_1 ^ * $

$ \ Rightarrow S_2 ^ * \ subseteq S_1 ^ * $

Định lý

Gọi C là một hình nón lồi không rỗng, khi đó $ C = C ^ ** $

Bằng chứng

$ C = C ^ {**} $ theo bổ đề trước.

Để chứng minh: $ x \ in C ^ {**} \ subseteq C $

Cho $ x \ trong C ^ {**} $ và cho $ x \ notin C $

Sau đó, theo định lý tách cơ bản, tồn tại một vectơ $ p \ neq 0 $ và một vô hướng $ \ alpha $ sao cho $ p ^ Ty \ leq \ alpha, \ forall y \ in C $

Do đó, $ p ^ Tx> \ alpha $

Nhưng vì $ \ left (y = 0 \ right) \ in C $ và $ p ^ Ty \ leq \ alpha, \ forall y \ in C \ Rightarrow \ alpha \ geq 0 $ và $ p ^ Tx> 0 $

Nếu $ p \ notin C ^ * $, thì tồn tại một số $ \ bar {y} \ trong C $ sao cho $ p ^ T \ bar {y}> 0 $ và $ p ^ T \ left (\ lambda \ bar {y} \ right) $ có thể lớn tùy ý bằng cách lấy $ \ lambda $ đủ lớn.

Điều này mâu thuẫn với thực tế là $ p ^ Ty \ leq \ alpha, \ forall y \ in C $

Do đó, $ p \ in C ^ * $

Vì $ x \ in C ^ * = \ left \ {q: q ^ Tp \ leq 0, \ forall p \ in C ^ * \ right \} $

Do đó, $ x ^ Tp \ leq 0 \ Rightarrow p ^ Tx \ leq 0 $

Nhưng $ p ^ Tx> \ alpha $

Như vậy là suy nghĩ.

Do đó, $ x \ trong C $

Do đó $ C = C ^ {**} $.

Một điểm có dạng $ \ alpha_1x_1 + \ alpha_2x_2 + .... + \ alpha_nx_n $ với $ \ alpha_1, \ alpha_2, ..., \ alpha_n \ geq 0 $ được gọi là kết hợp conic của $ x_1, x_2, ..., x_n. $

• Nếu $ x_i $ nằm trong hình nón lồi C, thì mọi tổ hợp hình nón của $ x_i $ cũng thuộc C.

• Tập hợp C là một hình nón lồi nếu nó chứa tất cả các tổ hợp conic của các phần tử của nó.

Conic Hull

Vỏ tàu conic được định nghĩa là một tập hợp tất cả các tổ hợp conic của một tập S cho trước và được ký hiệu là coni (S).

Do đó, $ coni \ left (S \ right) = \ left \ {\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i: x_i \ in S, \ lambda_i \ in \ mathbb {R}, \ lambda_i \ geq 0, i = 1,2, ... \ right \} $

• Vỏ tàu hình nón là một tập hợp lồi.
• Nguồn gốc luôn thuộc về vỏ tàu hình nón.

Một tập hợp trong $ \ mathbb {R} ^ n $ được cho là đa diện nếu nó là giao của một số hữu hạn các nửa không gian đóng, tức là,

$ S = \ left \ {x \ in \ mathbb {R} ^ n: p_ {i} ^ {T} x \ leq \ alpha_i, i = 1,2, ...., n \ right \} $

Ví dụ,

• $ \ left \ {x \ in \ mathbb {R} ^ n: AX = b \ right \} $

• $ \ left \ {x \ in \ mathbb {R} ^ n: AX \ leq b \ right \} $

• $ \ left \ {x \ in \ mathbb {R} ^ n: AX \ geq b \ right \} $

Hình nón đa diện

Một tập hợp trong $ \ mathbb {R} ^ n $ được cho là hình nón đa diện nếu nó là giao của một số hữu hạn của nửa không gian chứa gốc, tức là $ S = \ left \ {x \ in \ mathbb { R} ^ n: p_ {i} ^ {T} x \ leq 0, i = 1, 2, ... \ right \} $

Polytope

Đa giác là một tập hợp đa diện có giới hạn.

Nhận xét

• Đa giác là một khối lồi của một tập hợp hữu hạn các điểm.
• Một hình nón đa diện được tạo bởi một tập hữu hạn các vectơ.
• Tập hợp đa diện là tập hợp đóng.
• Một tập hợp đa diện là một tập hợp lồi.

Cho S là một tập lồi trong $ \ mathbb {R} ^ n $. Một vectơ $ x \ trong S $ được cho là điểm cực trị của S nếu $ x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2 $ với $ x_1, x_2 \ trong S $ và $ \ lambda \ trong \ left (0, 1 \ right) \ Rightarrow x = x_1 = x_2 $.

Thí dụ

Step 1 - $ S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 1 \ right \ } $

Điểm cực trị, $ E = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_ {1} ^ {2} + x_ {2} ^ {2} = 1 \ right \} $

Step 2 - $ S = \ left \ {\ left (x_1, x_2 \ right) \ in \ mathbb {R} ^ 2: x_1 + x_2 <2, -x_1 + 2x_2 \ leq 2, x_1, x_2 \ geq 0 \ right \ } $

Điểm cực hạn, $ E = \ left \ {\ left (0, 0 \ right), \ left (2, 0 \ right), \ left (0, 1 \ right), \ left (\ frac {2} {3 }, \ frac {4} {3} \ right) \ right \} $

Step 3 - S là đa giác được tạo bởi các điểm $ \ left \ {\ left (0,0 \ right), \ left (1,1 \ right), \ left (1,3 \ right), \ left (-2, 4 \ right), \ left (0,2 \ right) \ right \} $

Điểm cực trị, $ E = \ left \ {\ left (0,0 \ right), \ left (1,1 \ right), \ left (1,3 \ right), \ left (-2,4 \ right) \ right \} $

Nhận xét

• Bất kỳ điểm nào của tập lồi S, có thể được biểu diễn dưới dạng tổ hợp lồi của các điểm cực trị của nó.

• Nó chỉ đúng với các tập đóng và có giới hạn trong $ \ mathbb {R} ^ n $.

• Nó có thể không đúng với các tập hợp không bị ràng buộc.

k điểm cực trị

Một điểm trong tập lồi được gọi là k cực trị nếu và chỉ khi nó là điểm bên trong của tập lồi k chiều trong S và nó không phải là điểm trong của tập lồi có chiều (k + 1) trong S. Về cơ bản, đối với tập lồi S, k điểm cực trị tạo thành mặt thoáng k chiều.

Cho S là một tập lồi đóng trong $ \ mathbb {R} ^ n $. Vectơ khác 0 $ d \ in \ mathbb {R} ^ n $ được gọi là hướng của S nếu với mỗi $ x \ in S, x + \ lambda d \ in S, \ forall \ lambda \ geq 0. $

• Hai hướng $ d_1 $ và $ d_2 $ của S được gọi là khác biệt nếu $ d \ neq \ alpha d_2 $ cho $ \ alpha> 0 $.

• Hướng $ d $ của $ S $ được cho là hướng cực trị nếu nó không thể được viết dưới dạng kết hợp tuyến tính dương của hai hướng phân biệt, tức là nếu $ d = \ lambda _1d_1 + \ lambda _2d_2 $ cho $ \ lambda _1, \ lambda _2> 0 $, sau đó $ d_1 = \ alpha d_2 $ cho một số $ \ alpha $.

• Bất kỳ hướng nào khác có thể được biểu thị như một sự kết hợp tích cực của các hướng cực trị.

• Đối với tập lồi $ S $, hướng d sao cho $ x + \ lambda d \ in S $ cho một số $ x \ in S $ và tất cả $ \ lambda \ geq0 $ được gọi recessive với giá $ S $.

• Gọi E là tập hợp các điểm mà một hàm nào đó $ f: S \ quét phải $ trên một tập lồi không rỗng S trong $ \ mathbb {R} ^ n $ đạt cực đại, thì $ E $ được gọi là mặt tiếp xúc của $ S $. Hướng của các mặt tiếp xúc được gọi là hướng tiếp xúc.

• Tia có phương là phương cực gọi là tia cực viễn.

Thí dụ

Xem xét hàm $ f \ left (x \ right) = y = \ left | x \ right | $, trong đó $ x \ in \ mathbb {R} ^ n $. Gọi d là vectơ đơn vị trong $ \ mathbb {R} ^ n $

Khi đó, d là hướng cho hàm f vì với mọi $ \ lambda \ geq 0, x + \ lambda d \ in f \ left (x \ right) $.

Cho $ f: S \ rightarrow \ mathbb {R} $, trong đó S là tập lồi khác rỗng trong $ \ mathbb {R} ^ n $, sau đó $ f \ left (x \ right) $ được cho là lồi trên S if $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left ( x_2 \ right), \ forall \ lambda \ in \ left (0,1 \ right) $.

Mặt khác, Giả sử $ f: S \ rightarrow \ mathbb {R} $, trong đó S là tập lồi khác rỗng trong $ \ mathbb {R} ^ n $, thì $ f \ left (x \ right) $ được cho là bị lõm trên S nếu $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ geq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right ) f \ left (x_2 \ right), \ forall \ lambda \ in \ left (0, 1 \ right) $.

Giả sử $ f: S \ rightarrow \ mathbb {R} $ trong đó S là tập lồi khác rỗng trong $ \ mathbb {R} ^ n $, thì $ f \ left (x \ right) $ được cho là tập lồi hoàn toàn trên S if $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) <\ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right), \ forall \ lambda \ in \ left (0, 1 \ right) $.

Giả sử $ f: S \ rightarrow \ mathbb {R} $ trong đó S là tập lồi khác rỗng trong $ \ mathbb {R} ^ n $, sau đó $ f \ left (x \ right) $ được cho là hoàn toàn lõm trên S if $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right)> \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right), \ forall \ lambda \ in \ left (0, 1 \ right) $.

Ví dụ

• Một hàm tuyến tính vừa lồi vừa lõm.

• $ f \ left (x \ right) = \ left | x \ right | $ là một hàm lồi.

• $ f \ left (x \ right) = \ frac {1} {x} $ là một hàm lồi.

Định lý

Cho $ f_1, f_2, ..., f_k: \ mathbb {R} ^ n \ rightarrow \ mathbb {R} $ là các hàm lồi. Hãy xem xét hàm $ f \ left (x \ right) = \ displaystyle \ sum \ limit_ {j = 1} ^ k \ alpha_jf_j \ left (x \ right) $ trong đó $ \ alpha_j> 0, j = 1, 2 ,. ..k, $ thì $ f \ left (x \ right) $ là một hàm lồi.

Bằng chứng

Vì $ f_1, f_2, ... f_k $ là các hàm lồi

Do đó, $ f_i \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f_i \ left (x_1 \ right) + \ left (1- \ lambda \ right) f_i \ left (x_2 \ right), \ forall \ lambda \ in \ left (0, 1 \ right) $ và $ i = 1, 2, ...., k $

Hãy xem xét hàm $ f \ left (x \ right) $.

Vì thế,

$ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) $

$ = \ displaystyle \ sum \ limit_ {j = 1} ^ k \ alpha_jf_j \ left (\ lambda x_1 + 1- \ lambda \ right) x_2 \ leq \ displaystyle \ sum \ limit_ {j = 1} ^ k \ alpha_j \ lambda f_j \ left (x_1 \ right) + \ left (1- \ lambda \ right) f_j \ left (x_2 \ right) $

$ \ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda \ left (\ displaystyle \ sum \ limit_ {j = 1} ^ k \ alpha _jf_j \ left ( x_1 \ right) \ right) + \ left (\ displaystyle \ sum \ limit_ {j = 1} ^ k \ alpha _jf_j \ left (x_2 \ right) \ right) $

$ \ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_2 \ right) \ leq \ left (1- \ lambda \ right) f \ trái (x_2 \ phải) $

Do đó, $ f \ left (x \ right) $ là một hàm lồi.

Định lý

Đặt $ f \ left (x \ right) $ là một hàm lồi trên một tập lồi $ S \ subset \ mathbb {R} ^ n $ thì một cực tiểu cục bộ của $ f \ left (x \ right) $ trên S là một cực tiểu toàn cục.

Bằng chứng

Đặt $ \ hat {x} $ là cực tiểu cục bộ cho $ f \ left (x \ right) $ và $ \ hat {x} $ không phải là cực tiểu cục bộ.

do đó, $ \ tồn tại \ hat {x} \ trong S $ sao cho $ f \ left (\ bar {x} \ right) <f \ left (\ hat {x} \ right) $

Vì $ \ hat {x} $ là cực tiểu cục bộ nên tồn tại vùng lân cận $ N_ \ varepsilon \ left (\ hat {x} \ right) $ sao cho $ f \ left (\ hat {x} \ right) \ leq f \ left (x \ right), \ forall x \ in N_ \ varepsilon \ left (\ hat {x} \ right) \ cap S $

Nhưng $ f \ left (x \ right) $ là một hàm lồi trên S, do đó đối với $ \ lambda \ in \ left (0, 1 \ right) $

chúng ta có $ \ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} \ leq \ lambda f \ left (\ hat {x} \ right) + \ left (1- \ lambda \ right) f \ left (\ bar {x} \ right) $

$ \ Rightarrow \ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} <\ lambda f \ left (\ hat {x} \ right) + \ left (1- \ lambda \ phải) f \ left (\ hat {x} \ right) $

$ \ Rightarrow \ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} <f \ left (\ hat {x} \ right), \ forall \ lambda \ in \ left (0 , 1 \ phải) $

Nhưng đối với một số $ \ lambda <1 $ nhưng gần bằng 1, chúng ta có

$ \ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} \ in N_ \ varepsilon \ left (\ hat {x} \ right) \ cap S $ và $ f \ left ( \ lambda \ hat {x} + \ left (1- \ lambda \ right) \ bar {x} \ right) <f \ left (\ bar {x} \ right) $

đó là một mâu thuẫn.

Do đó, $ \ bar {x} $ là cực tiểu toàn cục.

Epigraph

đặt S là tập con không rỗng trong $ \ mathbb {R} ^ n $ và đặt $ f: S \ rightarrow \ mathbb {R} $ thì epigraph của f được ký hiệu là epi (f) hoặc $ E_f $ là một tập con trong tổng số $ \ mathbb {R} ^ n + 1 $ được xác định bởi $ E_f = \ left \ {\ left (x, \ alpha \ right): x \ in \ mathbb {R} ^ n, \ alpha \ in \ mathbb { R}, f \ left (x \ right) \ leq \ alpha \ right \} $

Chữ viết

đặt S là một tập con không rỗng trong $ \ mathbb {R} ^ n $ và đặt $ f: S \ rightarrow \ mathbb {R} $, sau đó dấu gạch ngang của f được ký hiệu là hyp (f) hoặc $ H_f = \ left \ {\ left (x, \ alpha \ right): x \ in \ mathbb {R} ^ n, \ alpha \ in \ mathbb {R} ^ n, \ alpha \ in \ mathbb {R}, f \ left ( x \ right) \ geq \ alpha \ right \} $

Định lý

Gọi S là một tập lồi khác rỗng trong $ \ mathbb {R} ^ n $ và đặt $ f: S \ rightarrow \ mathbb {R} ^ n $, khi đó f là lồi nếu và chỉ khi biểu đồ $ E_f $ là một tập hợp lồi.

Bằng chứng

Cho f là một hàm lồi.

Để chỉ ra $ E_f $ là một tập hợp lồi.

Để $ \ left (x_1, \ alpha_1 \ right), \ left (x_2, \ alpha_2 \ right) \ trong E_f, \ lambda \ in \ left (0, 1 \ right) $

Để hiển thị $ \ lambda \ left (x_1, \ alpha_1 \ right) + \ left (1- \ lambda \ right) \ left (x_2, \ alpha_2 \ right) \ trong E_f $

$ \ Rightarrow \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2, \ lambda \ alpha_1 + \ left (1- \ lambda \ right) \ alpha_2 \ right] \ trong E_f $

$ f \ left (x_1 \ right) \ leq \ alpha _1, f \ left (x_2 \ right) \ leq \ alpha _2 $

Do đó, $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right) $

$ \ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda \ alpha_1 + \ left (1- \ lambda \ right) \ alpha_2 $

ngược

Cho $ E_f $ là một tập lồi.

Để chứng tỏ f là lồi.

tức là, để hiển thị nếu $ x_1, x_2 \ in S, \ lambda \ left (0, 1 \ right) $

$ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right) $

Cho $ x_1, x_2 \ in S, \ lambda \ in \ left (0, 1 \ right), f \ left (x_1 \ right), f \ left (x_2 \ right) \ in \ mathbb {R} $

Vì $ E_f $ là một tập hợp lồi, $ \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2, \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) \ phải) f \ left (x_2 \ right) \ trong E_f $

Do đó, $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right) $

Gọi S là một tập lồi khác rỗng trong $ \ mathbb {R} ^ n $ và $ f: S \ rightarrow \ mathbb {R} ^ n $. Khi đó f lồi nếu và chỉ khi với mỗi số nguyên $ k> 0 $

$ x_1, x_2, ... x_k \ in S, \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_i = 1, \ lambda_i \ geq 0, \ forall i = 1,2, s, k $, chúng ta có $ f \ left (\ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda_ix_i \ right) \ leq \ displaystyle \ sum \ limit_ {i = 1} ^ k \ lambda _if \ left (x \ right) $

Bằng chứng

Bằng quy nạp trên k.

$ k = 1: x_1 \ in S $ Do đó $ f \ left (\ lambda_1 x_1 \ right) \ leq \ lambda_i f \ left (x_1 \ right) $ vì $ \ lambda_i = 1 $.

$ k = 2: \ lambda_1 + \ lambda_2 = 1 $ và $ x_1, x_2 \ tính bằng S $

Do đó, $ \ lambda_1x_1 + \ lambda_2x_2 \ bằng S $

Do đó theo định nghĩa, $ f \ left (\ lambda_1 x_1 + \ lambda_2 x_2 \ right) \ leq \ lambda _1f \ left (x_1 \ right) + \ lambda _2f \ left (x_2 \ right) $

Giả sử câu lệnh đúng với $ n <k $

Vì thế,

$ f \ left (\ lambda_1 x_1 + \ lambda_2 x_2 + .... + \ lambda_k x_k \ right) \ leq \ lambda_1 f \ left (x_1 \ right) + \ lambda_2 f \ left (x_2 \ right) + ... + \ lambda_k f \ left (x_k \ right) $

$ k = n + 1: $ Cho $ x_1, x_2, .... x_n, x_ {n + 1} \ trong S $ và $ \ displaystyle \ sum \ limit_ {i = 1} ^ {n + 1} = 1 đô la

Do đó $ \ mu_1x_1 + \ mu_2x_2 + ....... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ tính bằng S $

do đó, $ f \ left (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right) $

$ = f \ left (\ left (\ mu_1 + \ mu_2 + ... + \ mu_n \ right) \ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n} {\ mu_1 + \ mu_2 + \ mu_3} + \ mu_ {n + 1} x_ {n + 1} \ right) $

$ = f \ left (\ mu_y + \ mu_ {n + 1} x_ {n + 1} \ right) $ trong đó $ \ mu = \ mu_1 + \ mu_2 + ... + \ mu_n $ và

$ y = \ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n} {\ mu_1 + \ mu_2 + ... + \ mu_n} $ và cả $ \ mu_1 + \ mu_ {n + 1} = 1, y \ bằng S $

$ \ Rightarrow f \ left (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right) \ leq \ mu f \ left (y \ right) + \ mu_ {n +1} f \ left (x_ {n + 1} \ right) $

$ \ Rightarrow f \ left (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right) \ leq $

$ \ left (\ mu_1 + \ mu_2 + ... + \ mu_n \ right) f \ left (\ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n} {\ mu_1 + \ mu_2 + ... + \ mu_n} \ right) + \ mu_ {n + 1} f \ left (x_ {n + 1} \ right) $

$ \ Rightarrow f \ left (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right) \ leq \ left (\ mu_1 + \ mu_2 + ... + \ mu_n \ đúng) $

$ \ left [\ frac {\ mu_1} {\ mu_1 + \ mu_2 + ... + \ mu_n} f \ left (x_1 \ right) + ... + \ frac {\ mu_n} {\ mu_1 + \ mu_2 + ... + \ mu_n} f \ left (x_n \ right) \ right] + \ mu_ {n + 1} f \ left (x_ {n + 1} \ right) $

$ \ Rightarrow f \ left (\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right) \ leq \ mu_1f \ left (x_1 \ right) + \ mu_2f \ left ( x_2 \ right) + .... $

Do đó đã được chứng minh.

Đặt S là một tập mở không trống trong $ \ mathbb {R} ^ n $, thì $ f: S \ rightarrow \ mathbb {R} $ được cho là có thể phân biệt được với $ \ hat {x} \ trong S $ nếu tồn tại một vectơ $ \ bigtriangledown f \ left (\ hat {x} \ right) $ được gọi là vectơ gradient và một hàm $ \ alpha: \ mathbb {R} ^ n \ rightarrow \ mathbb {R} $ sao cho

$ f \ left (x \ right) = f \ left (\ hat {x} \ right) + \ bigtriangledown f \ left (\ hat {x} \ right) ^ T \ left (x- \ hat {x} \ phải) + \ left \ | x = \ hat {x} \ right \ | \ alpha \ left (\ hat {x}, x- \ hat {x} \ right), \ forall x \ in S $ ở đâu

$ \ alpha \ left (\ hat {x}, x- \ hat {x} \ right) \ rightarrow 0 \ bigtriangledown f \ left (\ hat {x} \ right) = \ left [\ frac {\ part f} {\ một phần x_1} \ frac {\ một phần f} {\ một phần x_2} ... \ frac {\ một phần f} {\ một phần x_n} \ right] _ {x = \ hat {x}} ^ {T} $

Định lý

đặt S là một tập lồi mở, không rỗng trong $ \ mathbb {R} ^ n $ và để $ f: S \ rightarrow \ mathbb {R} $ có thể phân biệt được trên S. Khi đó, f là lồi nếu và chỉ khi với $ x_1, x_2 \ in S, \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) \ leq f \ left (x_1 \ right) -f \ left (x_2 \ right) $

Bằng chứng

Cho f là một hàm lồi. tức là với $ x_1, x_2 \ in S, \ lambda \ in \ left (0, 1 \ right) $

$ f \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right] \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right) $

$ \ Rightarrow f \ left [\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right] \ leq \ lambda \ left (f \ left (x_1 \ right) -f \ left (x_2 \ right) \ right ) + f \ left (x_2 \ right) $

$ \ Rightarrow \ lambda \ left (f \ left (x_1 \ right) -f \ left (x_2 \ right) \ right) \ geq f \ left (x_2 + \ lambda \ left (x_1-x_2 \ right) \ right) - f \ left (x_2 \ right) $

$ \ Rightarrow \ lambda \ left (f \ left (x_1 \ right) -f \ left (x_2 \ right) \ right) \ geq f \ left (x_2 \ right) + \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) \ lambda + $

$ \ left \ | \ lambda \ left (x_1-x_2 \ right) \ right \ | \ alpha \ left (x_2, \ lambda \ left (x_1 - x_2 \ right) -f \ left (x_2 \ right) \ right) $

trong đó $ \ alpha \ left (x_2, \ lambda \ left (x_1 - x_2 \ right) \ right) \ rightarrow 0 $ dưới dạng $ \ lambda \ rightarrow 0 $

Chia cho $ \ lambda $ ở cả hai phía, ta được -

$ f \ left (x_1 \ right) -f \ left (x_2 \ right) \ geq \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) $

ngược

Cho $ x_1, x_2 \ in S, \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) \ leq f \ left (x_1 \ right) -f \ left (x_2 \ right) $

Để chứng tỏ rằng f là lồi.

Vì S là lồi nên $ x_3 = \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ in S, \ lambda \ in \ left (0, 1 \ right) $

Vì $ x_1, x_3 \ tính bằng S $, do đó

$ f \ left (x_1 \ right) -f \ left (x_3 \ right) \ geq \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1 -x_3 \ right) $

$ \ Rightarrow f \ left (x_1 \ right) -f \ left (x_3 \ right) \ geq \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1 - \ lambda x_1- \ left (1- \ lambda \ right) x_2 \ right) $

$ \ Rightarrow f \ left (x_1 \ right) -f \ left (x_3 \ right) \ geq \ left (1- \ lambda \ right) \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1 - x_2 \ right) $

Do đó, $ x_2, x_3 \ in S $

$ f \ left (x_2 \ right) -f \ left (x_3 \ right) \ geq \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_2-x_3 \ right) $

$ \ Rightarrow f \ left (x_2 \ right) -f \ left (x_3 \ right) \ geq \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_2- \ lambda x_1- \ left (1- \ lambda \ right) x_2 \ right) $

$ \ Rightarrow f \ left (x_2 \ right) -f \ left (x_3 \ right) \ geq \ left (- \ lambda \ right) \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1-x_2 \ đúng) $

Do đó, kết hợp các phương trình trên, chúng ta nhận được -

$ \ lambda \ left (f \ left (x_1 \ right) -f \ left (x_3 \ right) \ right) + \ left (1- \ lambda \ right) \ left (f \ left (x_2 \ right) -f \ left (x_3 \ right) \ right) \ geq 0 $

$ \ Rightarrow f \ left (x_3 \ right) \ leq \ lambda f \ left (x_1 \ right) + \ left (1- \ lambda \ right) f \ left (x_2 \ right) $

Định lý

cho S là một tập lồi mở khác rỗng trong $ \ mathbb {R} ^ n $ và để cho $ f: S \ rightarrow \ mathbb {R} $ có thể phân biệt được trên S, khi đó f lồi trên S nếu và chỉ khi cho bất kỳ $ x_1, x_2 \ in S, \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0 $

Bằng chứng

cho f là một hàm lồi, sau đó sử dụng định lý trước -

$ \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) \ leq f \ left (x_1 \ right) -f \ left (x_2 \ right) $ và

$ \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) \ leq f \ left (x_2 \ right) -f \ left (x_1 \ right) $

Cộng hai phương trình trên, ta được -

$ \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) + \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) \ leq 0 $

$ \ Rightarrow \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x_1-x_2 \ right) \ leq 0 $

$ \ Rightarrow \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0 $

ngược

Cho bất kỳ $ x_1, x_2 \ in S, \ left (\ bigtriangledown f \ left (x_2 \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0 $

Để chứng tỏ rằng f là lồi.

Giả sử $ x_1, x_2 \ trong S $, do đó theo định lý giá trị trung bình, $ \ frac {f \ left (x_1 \ right) -f \ left (x_2 \ right)} {x_1-x_2} = \ bigtriangledown f \ left ( x \ right), x \ in \ left (x_1-x_2 \ right) \ Rightarrow x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2 $ vì S là tập lồi.

$ \ Rightarrow f \ left (x_1 \ right) - f \ left (x_2 \ right) = \ left (\ bigtriangledown f \ left (x \ right) ^ T \ right) \ left (x_1-x_2 \ right) $

với $ x, x_1 $, chúng tôi biết -

$ \ left (\ bigtriangledown f \ left (x \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (x-x_1 \ right) \ geq 0 $

$ \ Rightarrow \ left (\ bigtriangledown f \ left (x \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2- x_1 \ right) \ geq 0 $

$ \ Rightarrow \ left (\ bigtriangledown f \ left (x \ right) - \ bigtriangledown f \ left (x_1 \ right) \ right) ^ T \ left (1- \ lambda \ right) \ left (x_2-x_1 \ right ) \ geq 0 $

$ \ Rightarrow \ bigtriangledown f \ left (x \ right) ^ T \ left (x_2-x_1 \ right) \ geq \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) $

Kết hợp các phương trình trên, ta được -

$ \ Rightarrow \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) \ leq f \ left (x_2 \ right) -f \ left (x_1 \ right) $

Do đó, sử dụng định lý cuối cùng, f là một hàm lồi.

Hai lần chức năng khác biệt

Gọi S là tập con khác rỗng của $ \ mathbb {R} ^ n $ và đặt $ f: S \ rightarrow \ mathbb {R} $ thì f được cho là có thể phân biệt hai lần tại $ \ bar {x} \ trong S $ nếu tồn tại vectơ $ \ bigtriangledown f \ left (\ bar {x} \ right), a \: nXn $ ma trận $ H \ left (x \ right) $ (được gọi là ma trận Hessian) và một hàm $ \ alpha: \ mathbb {R} ^ n \ rightarrow \ mathbb {R} $ sao cho $ f \ left (x \ right) = f \ left (\ bar {x} + x- \ bar {x} \ right) = f \ left (\ bar {x} \ right) + \ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x} \ right) + \ frac {1} {2} \ left (x- \ bar {x} \ right) H \ left (\ bar {x} \ right) \ left (x- \ bar {x} \ right) $

trong đó $ \ alpha \ left (\ bar {x}, x- \ bar {x} \ right) \ rightarrow Oasx \ rightarrow \ bar {x} $

Định lý

Cho f là hàm phân biệt hai lần. Nếu $ \ bar {x} $ là cực tiểu cục bộ thì $ \ bigtriangledown f \ left (\ bar {x} \ right) = 0 $ và ma trận Hessian $ H \ left (\ bar {x} \ right) $ là một bán kỳ dương.

Bằng chứng

Cho $ d \ in \ mathbb {R} ^ n $. Vì f phân biệt hai lần tại $ \ bar {x} $.

Vì thế,

$ f \ left (\ bar {x} + \ lambda d \ right) = f \ left (\ bar {x} \ right) + \ lambda \ bigtriangledown f \ left (\ bar {x} \ right) ^ T d + \ lambda ^ 2d ^ TH \ left (\ bar {x} \ right) d + \ lambda ^ 2d ^ TH \ left (\ bar {x} \ right) d + $

$ \ lambda ^ 2 \ left \ | d \ right \ | ^ 2 \ beta \ left (\ bar {x}, \ lambda d \ right) $

Nhưng $ \ bigtriangledown f \ left (\ bar {x} \ right) = 0 $ và $ \ beta \ left (\ bar {x}, \ lambda d \ right) \ rightarrow 0 $ as $ \ lambda \ rightarrow 0 $

$ \ Rightarrow f \ left (\ bar {x} + \ lambda d \ right) -f \ left (\ bar {x} \ right) = \ lambda ^ 2d ^ TH \ left (\ bar {x} \ right) d $

Vì $ \ bar {x} $ là cực tiểu cục bộ nên tồn tại $ \ delta> 0 $ sao cho $ f \ left (x \ right) \ leq f \ left (\ bar {x} + \ lambda d \ right ), \ forall \ lambda \ in \ left (0, \ delta \ right) $

Định lý

Giả sử $ f: S \ rightarrow \ mathbb {R} ^ n $ trong đó $ S \ subset \ mathbb {R} ^ n $ có thể phân biệt hai lần so với S. Nếu $ \ bigtriangledown f \ left (x \ right) = 0 $ và $ H \ left (\ bar {x} \ right) $ là bán xác định dương, đối với tất cả $ x \ tính bằng S $, thì $ \ bar {x} $ là giải pháp tối ưu toàn cầu.

Bằng chứng

Vì $ H \ left (\ bar {x} \ right) $ là bán xác định dương, f là hàm lồi trên S. Vì f là hàm phân biệt và lồi tại $ \ bar {x} $

$ \ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x} \ right) \ leq f \ left (x \ right) -f \ left (\ bar {x} \ right), \ forall x \ in S $

Vì $ \ bigtriangledown f \ left (\ bar {x} \ right) = 0, f \ left (x \ right) \ geq f \ left (\ bar {x} \ right) $

Do đó, $ \ bar {x} $ là một tối ưu hóa toàn cầu.

Định lý

Giả sử $ \ bar {x} \ in S $ là một giải pháp tối ưu cục bộ cho bài toán $ f: S \ rightarrow \ mathbb {R} $ trong đó S là tập con không rỗng của $ \ mathbb {R} ^ n $ và S là tập lồi. $ min \: f \ left (x \ right) $ trong đó $ x \ tính bằng S $.

Sau đó:

• $ \ bar {x} $ là một giải pháp tối ưu toàn cầu.

• Nếu $ \ bar {x} $ là cực tiểu cục bộ hoàn toàn hoặc f là hàm lồi hoàn toàn, thì $ \ bar {x} $ là giải pháp tối ưu toàn cục duy nhất và cũng là cực tiểu cục bộ mạnh.

Bằng chứng

Hãy để $ \ bar {x} $ là một giải pháp tối ưu toàn cầu khác cho vấn đề sao cho $ x \ neq \ bar {x} $ và $ f \ left (\ bar {x} \ right) = f \ left (\ hat { x} \ right) $

Vì $ \ hat {x}, \ bar {x} \ in S $ và S là lồi nên $ \ frac {\ hat {x} + \ bar {x}} {2} \ in S $ và f là đúng lồi lõm.

$ \ Rightarrow f \ left (\ frac {\ hat {x} + \ bar {x}} {2} \ right) <\ frac {1} {2} f \ left (\ bar {x} \ right) + \ frac {1} {2} f \ left (\ hat {x} \ right) = f \ left (\ hat {x} \ right) $

Đây là sự mâu thuẫn.

Do đó, $ \ hat {x} $ là một giải pháp tối ưu toàn cầu duy nhất.

Hệ quả

Gọi $ f: S \ subset \ mathbb {R} ^ n \ rightarrow \ mathbb {R} $ là một hàm lồi phân biệt trong đó $ \ phi \ neq S \ subset \ mathbb {R} ^ n $ là một tập lồi. Hãy xem xét vấn đề $ min f \ left (x \ right), x \ in S $, thì $ \ bar {x} $ là một giải pháp tối ưu nếu $ \ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x} \ right) \ geq 0, \ forall x \ in S. $

Bằng chứng

Hãy để $ \ bar {x} $ là một giải pháp tối ưu, tức là $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ in S $

$ \ Rightarrow f \ left (x \ right) = f \ left (\ bar {x} \ right) \ geq 0 $

$ f \ left (x \ right) = f \ left (\ bar {x} \ right) + \ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x} \ phải) + \ left \ | x- \ bar {x} \ right \ | \ alpha \ left (\ bar {x}, x- \ bar {x} \ right) $

trong đó $ \ alpha \ left (\ bar {x}, x- \ bar {x} \ right) \ rightarrow 0 $ dưới dạng $ x \ rightarrow \ bar {x} $

$ \ Rightarrow f \ left (x \ right) -f \ left (\ bar {x} \ right) = \ bigtriangledown f \ left (\ bar {x} \ right) ^ T \ left (x- \ bar {x } \ right) \ geq 0 $

Hệ quả

Đặt f là một hàm lồi có thể phân biệt tại $ \ bar {x} $, sau đó $ \ bar {x} $ là giá trị nhỏ nhất toàn cục $ \ bigtriangledown f \ left (\ bar {x} \ right) = 0 $

Ví dụ

• $ f \ left (x \ right) = \ left (x ^ 2-1 \ right) ^ {3}, x \ in \ mathbb {R} $.

  $ \ bigtriangledown f \ left (x \ right) = 0 \ Rightarrow x = -1,0,1 $.

  $ \ bigtriangledown ^ 2f \ left (\ pm 1 \ right) = 0, \ bigtriangledown ^ 2 f \ left (0 \ right) = 6> 0 $.

  $ f \ left (\ pm 1 \ right) = 0, f \ left (0 \ right) = - 1 $

  Do đó, $ f \ left (x \ right) \ geq -1 = f \ left (0 \ right) \ Rightarrow f \ left (0 \ right) \ leq f \ left (x \ right) \ forall x \ in \ toánbb {R} $

• $ f \ left (x \ right) = x \ log x $ được xác định trên $ S = \ left \ {x \ in \ mathbb {R}, x> 0 \ right \} $.

  $ {f} 'x = 1 + \ log x $

  $ {f} '' x = \ frac {1} {x}> 0 $

  Do đó, hàm này là hàm lồi.

• $ f \ left (x \ right) = e ^ {x}, x \ in \ mathbb {R} $ hoàn toàn lồi.

Cho $ f: S \ rightarrow \ mathbb {R} $ trong đó $ S \ subset \ mathbb {R} ^ n $ là một tập lồi không rỗng. Hàm f được cho là lồi nếu với mỗi $ x_1, x_2 \ trong S $, chúng ta có $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}, \ lambda \ in \ left (0, 1 \ right) $

Ví dụ: $ f \ left (x \ right) = x ^ {3} $

Cho $ f: S \ rightarrow R $ trong đó $ S \ subset \ mathbb {R} ^ n $ là một tập lồi không rỗng. Hàm f được cho là chuẩn lồi nếu với mỗi $ x_1, x_2 \ trong S $, chúng ta có $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ geq min \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}, \ lambda \ in \ left (0, 1 \ right) $

Nhận xét

• Mọi hàm lồi đều là quasiconvex nhưng điều ngược lại không đúng.
• Một hàm có cả mặt phẳng và mặt lõm được gọi là quasimonotone.

Định lý

Cho $ f: S \ rightarrow \ mathbb {R} $ và S là một tập lồi không rỗng trong $ \ mathbb {R} ^ n $. Hàm f là chuẩn lồi khi và chỉ khi $ S _ {\ alpha} = \ left (x \ in S: f \ left (x \ right) \ leq \ alpha \ right \} $ lồi cho mỗi số thực \ alpha $

Bằng chứng

Cho f là mặt phẳng lồi trên S.

Cho $ x_1, x_2 \ in S _ {\ alpha} $ do đó $ x_1, x_2 \ in S $ và $ max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \} \ leq \ alpha $

Đặt $ \ lambda \ in \ left (0, 1 \ right) $ và để $ x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ leq max \ left \ {f \ left (x_1 \ right) , f \ left (x_2 \ right) \ right \} \ Rightarrow x \ in S $

Do đó, $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \} \ leq \ alpha $

Do đó, $ S _ {\ alpha} $ là tập lồi.

ngược

Cho $ S _ {\ alpha} $ lồi với mỗi $ \ alpha $

$ x_1, x_2 \ in S, \ lambda \ in \ left (0,1 \ right) $

$ x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2 $

Cho $ x = \ lambda x_1 + \ left (1- \ lambda \ right) x_2 $

Đối với $ x_1, x_2 \ in S _ {\ alpha}, \ alpha = max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \} $

$ \ Rightarrow \ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ trong S _ {\ alpha} $

$ \ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq \ alpha $

Do đó đã chứng minh.

Định lý

Cho $ f: S \ rightarrow \ mathbb {R} $ và S là một tập lồi không rỗng trong $ \ mathbb {R} ^ n $. Hàm f là chuẩn xác định nếu và chỉ khi $ S _ {\ alpha} = \ left \ {x \ trong S: f \ left (x \ right) \ geq \ alpha \ right \} $ lồi cho mỗi số thực $ \ alpha $.

Định lý

Cho $ f: S \ rightarrow \ mathbb {R} $ và S là một tập lồi không rỗng trong $ \ mathbb {R} ^ n $. Hàm f là quasimonotone nếu và chỉ khi $ S _ {\ alpha} = \ left \ {x \ trong S: f \ left (x \ right) = \ alpha \ right \} $ lồi cho mỗi số thực $ \ alpha $.

Định lý

Gọi S là một tập lồi không rỗng trong $ \ mathbb {R} ^ n $ và $ f: S \ rightarrow \ mathbb {R} $ có thể phân biệt được trên S, khi đó f là chuẩn tinh nếu và chỉ khi với $ x_1, x_2 bất kỳ \ trong S $ và $ f \ left (x_1 \ right) \ leq f \ left (x_2 \ right) $, chúng ta có $ \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_2-x_1 \ right) \ leq 0 $

Bằng chứng

Cho f là một hàm quasiconvex.

Đặt $ x_1, x_2 \ trong S $ sao cho $ f \ left (x_1 \ right) \ leq f \ left (x_2 \ right) $

Theo khả năng phân biệt của f tại $ x_2, \ lambda \ in \ left (0, 1 \ right) $

$ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) = f \ left (x_2 + \ lambda \ left (x_1-x_2 \ right) \ right) = f \ left (x_2 \ right ) + \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) $

$ + \ lambda \ left \ | x_1-x_2 \ right \ | \ alpha \ left (x_2, \ lambda \ left (x_1-x_2 \ right) \ right) $

$ \ Rightarrow f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) -f \ left (x_2 \ right) -f \ left (x_2 \ right) = \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) $

$ + \ lambda \ left \ | x_1-x_2 \ right \ | \ alpha \ left (x2, \ lambda \ left (x_1-x_2 \ right) \ right) $

Nhưng vì f là mặt phẳng lồi nên $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq f \ left (x_2 \ right) $

$ \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) + \ lambda \ left \ | x_1-x_2 \ right \ | \ alpha \ left (x_2, \ lambda \ left (x_1, x_2 \ right) \ right) \ leq 0 $

Nhưng $ \ alpha \ left (x_2, \ lambda \ left (x_1, x_2 \ right) \ right) \ rightarrow 0 $ là $ \ lambda \ rightarrow 0 $

Do đó, $ \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1-x_2 \ right) \ leq 0 $

ngược

cho $ x_1, x_2 \ in S $ và $ f \ left (x_1 \ right) \ leq f \ left (x_2 \ right) $, $ \ bigtriangledown f \ left (x_2 \ right) ^ T \ left (x_1, x_2 \ right) \ leq 0 $

Để chỉ ra rằng f là mặt phẳng lồi, tức là $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) \ leq f \ left (x_2 \ right) $

Proof by contradiction

Giả sử có một $ x_3 = \ lambda x_1 + \ left (1- \ lambda \ right) x_2 $ sao cho $ f \ left (x_2 \ right) <f \ left (x_3 \ right) $ cho một số $ \ lambda \ in \ left (0, 1 \ right) $

Đối với $ x_2 $ và $ x_3, \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_2-x_3 \ right) \ leq 0 $

$ \ Rightarrow - \ lambda \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_2-x_3 \ right) \ leq 0 $

$ \ Rightarrow \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1-x_2 \ right) \ geq 0 $

Đối với $ x_1 $ và $ x_3, \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1-x_3 \ right) \ leq 0 $

$ \ Rightarrow \ left (1- \ lambda \ right) \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1-x_2 \ right) \ leq 0 $

$ \ Rightarrow \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1-x_2 \ right) \ leq 0 $

do đó, từ các phương trình trên, $ \ bigtriangledown f \ left (x_3 \ right) ^ T \ left (x_1-x_2 \ right) = 0 $

Xác định $ U = \ left \ {x: f \ left (x \ right) \ leq f \ left (x_2 \ right), x = \ mu x_2 + \ left (1- \ mu \ right) x_3, \ mu \ in \ left (0,1 \ right) \ right \} $

Do đó, chúng ta có thể tìm $ x_0 \ trong U $ sao cho $ x_0 = \ mu_0 x_2 = \ mu x_2 + \ left (1- \ mu \ right) x_3 $ cho một số $ \ mu _0 \ in \ left (0,1 \ right ) $ gần nhất với $ x_3 $ và $ \ hat {x} \ in \ left (x_0, x_1 \ right) $ sao cho theo định lý giá trị trung bình,

$$ \ frac {f \ left (x_3 \ right) -f \ left (x_0 \ right)} {x_3-x_0} = \ bigtriangledown f \ left (\ hat {x} \ right) $$

$$ \ Rightarrow f \ left (x_3 \ right) = f \ left (x_0 \ right) + \ bigtriangledown f \ left (\ hat {x} \ right) ^ T \ left (x_3-x_0 \ right) $$

$$ \ Rightarrow f \ left (x_3 \ right) = f \ left (x_0 \ right) + \ mu_0 \ lambda f \ left (\ hat {x} \ right) ^ T \ left (x_1-x_2 \ right) $ $

Vì $ x_0 $ là sự kết hợp của $ x_1 $ và $ x_2 $ và $ f \ left (x_2 \ right) <f \ left (\ hat {x} \ right) $

Bằng cách lặp lại quy trình bắt đầu, $ \ bigtriangledown f \ left (\ hat {x} \ right) ^ T \ left (x_1-x_2 \ right) = 0 $

Do đó, kết hợp các phương trình trên, chúng ta nhận được:

$$ f \ left (x_3 \ right) = f \ left (x_0 \ right) \ leq f \ left (x_2 \ right) $$

$$ \ Rightarrow f \ left (x_3 \ right) \ leq f \ left (x_2 \ right) $$

Do đó, nó là mâu thuẫn.

Ví dụ

Step 1 - $ f \ left (x \ right) = X ^ 3 $

$ Để f \ left (x_1 \ right) \ leq f \ left (x_2 \ right) $

$ \ Rightarrow x_ {1} ^ {3} \ leq x_ {2} ^ {3} \ Rightarrow x_1 \ leq x_2 $

$ \ bigtriangledown f \ left (x_2 \ right) \ left (x_1-x_2 \ right) = 3x_ {2} ^ {2} \ left (x_1-x_2 \ right) \ leq 0 $

Do đó, $ f \ left (x \ right) $ là mặt phẳng lồi.

Step 2 - $ f \ left (x \ right) = x_ {1} ^ {3} + x_ {2} ^ {3} $

Cho $ \ hat {x_1} = \ left (2, -2 \ right) $ và $ \ hat {x_2} = \ left (1, 0 \ right) $

do đó, $ f \ left (\ hat {x_1} \ right) = 0, f \ left (\ hat {x_2} \ right) = 1 \ Rightarrow f \ left (\ hat {x_1} \ right) \ setminus <f \ left (\ hat {x_2} \ right) $

Do đó, $ \ bigtriangledown f \ left (\ hat {x_2} \ right) ^ T \ left (\ hat {x_1} - \ hat {x_2} \ right) = \ left (3, 0 \ right) ^ T \ left (1, -2 \ phải) = 3> 0 $

Do đó $ f \ left (x \ right) $ không phải là mặt lồi.

Đặt $ f: S \ rightarrow \ mathbb {R} ^ n $ và S là một tập lồi không rỗng trong $ \ mathbb {R} ^ n $ thì f được cho là hàm quasicovex hoàn toàn nếu với mỗi $ x_1, x_2 \ trong S $ với $ f \ left (x_1 \ right) \ neq f \ left (x_2 \ right) $, chúng ta có $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) <max \: \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \} $

Nhận xét

• Mọi hàm quasiconvex đúng là lồi.
• Hàm quasiconvex chính xác không có nghĩa là quasiconvexity.
• Hàm chuẩn tinh có thể không phải là chuẩn tinh.
• Hàm Pseudoconvex là một hàm gần như hoàn toàn lồi.

Định lý

Gọi $ f: S \ rightarrow \ mathbb {R} ^ n $ là hàm gần như hoàn toàn và S là một tập lồi không rỗng trong $ \ mathbb {R} ^ n $. Xem xét vấn đề: $ min \: f \ left (x \ right), x \ bằng S $. Nếu $ \ hat {x} $ là giải pháp tối ưu cục bộ, thì $ \ bar {x} $ là giải pháp tối ưu toàn cục.

Bằng chứng

Để tồn tại $ \ bar {x} \ trong S $ sao cho $ f \ left (\ bar {x} \ right) \ leq f \ left (\ hat {x} \ right) $

Vì $ \ bar {x}, \ hat {x} \ in S $ và S là tập lồi, do đó,

$$ \ lambda \ bar {x} + \ left (1- \ lambda \ right) \ hat {x} \ in S, \ forall \ lambda \ in \ left (0,1 \ right) $$

Vì $ \ hat {x} $ là cực tiểu cục bộ nên $ f \ left (\ hat {x} \ right) \ leq f \ left (\ lambda \ bar {x} + \ left (1- \ lambda \ right) \ hat {x} \ right), \ forall \ lambda \ in \ left (0, \ delta \ right) $

Vì f là chuẩn tinh.

$$ f \ left (\ lambda \ bar {x} + \ left (1- \ lambda \ right) \ hat {x} \ right) <max \ left \ {f \ left (\ hat {x} \ right) , f \ left (\ bar {x} \ right) \ right \} = f \ left (\ hat {x} \ right) $$

Do đó, nó là mâu thuẫn.

Hàm quasicon lõm chính xác

Đặt $ f: S \ rightarrow \ mathbb {R} ^ n $ và S là một tập lồi không rỗng trong $ \ mathbb {R} ^ n $, thì f là hàm quasicovex đúng nếu với mỗi $ x_1, x_2 \ in S $ với $ f \ left (x_1 \ right) \ neq f \ left (x_2 \ right) $, chúng tôi có

$$ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right)> min \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \} $$.

Ví dụ

• $ f \ left (x \ right) = x ^ 2-2 $

  Đây là một hàm gần như hoàn toàn lồi vì nếu chúng ta lấy hai điểm $ x_1, x_2 $ bất kỳ trong miền thỏa mãn các ràng buộc trong định nghĩa $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) <max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \} $ Vì hàm đang giảm theo trục x âm và nó đang tăng theo trục x dương ( vì nó là một parabol).

• $ f \ left (x \ right) = - x ^ 2 $

  Đây không phải là một hàm chuẩn hoàn toàn vì nếu chúng ta lấy $ x_1 = 1 $ và $ x_2 = -1 $ và $ \ lambda = 0,5 $, thì $ f \ left (x_1 \ right) = - 1 = f \ left ( x_2 \ right) $ but $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) = 0 $ Do đó nó không thỏa mãn các điều kiện được nêu trong định nghĩa. Nhưng nó là một hàm quasicon lõm vì nếu chúng ta lấy hai điểm bất kỳ trong miền thỏa mãn các ràng buộc trong định nghĩa $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right)> min \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \} $. Khi hàm số đang tăng theo trục x âm và nó đang giảm theo trục x dương.

Gọi $ f: S \ rightarrow \ mathbb {R} ^ n $ và S là một tập lồi không rỗng trong $ \ mathbb {R} ^ n $ thì f là hàm chuẩn thực nếu với bất kỳ $ x_1, x_2 \ trong S $ với $ \ left (x_1 \ right) \ neq \ left (x_2 \ right) $, chúng ta có $ f \ left (\ lambda x_1 + \ left (1- \ lambda \ right) x_2 \ right) <max \: \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}, \ forall \ lambda \ in \ left (0,1 \ right) $

Định lý

Hàm quasiconvex $ f: S \ rightarrow \ mathbb {R} ^ n $ trên tập lồi không rỗng S trong $ \ mathbb {R} ^ n $ là hàm quasiconvex mạnh mẽ nếu nó không phải là hằng số trên một đoạn thẳng nối bất kỳ điểm của S.

Bằng chứng

Gọi f là hàm mặt lồi và nó không phải là hằng số trên một đoạn thẳng nối các điểm bất kỳ của S.

Giả sử f không phải là hàm mặt lồi mạnh.

Có $ x_1, x_2 \ in S $ với $ x_1 \ neq x_2 $ sao cho

$$ f \ left (z \ right) \ geq max \ left \ {f \ left (x_1 \ right), f \ left (x_2 \ right) \ right \}, \ forall z = \ lambda x_1 + \ left (1 - \ lambda \ right) x_2, \ lambda \ in \ left (0,1 \ right) $$

$ \ Rightarrow f \ left (x_1 \ right) \ leq f \ left (z \ right) $ và $ f \ left (x_2 \ right) \ leq f \ left (z \ right) $

Vì f không phải là hằng số nên $ \ left [x_1, z \ right] $ và $ \ left [z, x_2 \ right] $

Vì vậy, tồn tại $ u \ in \ left [x_1, z \ right] $ và $ v = \ left [z, x_2 \ right] $

$$ \ Rightarrow u = \ mu_1x_1 + \ left (1- \ mu_1 \ right) z, v = \ mu_2z + \ left (1- \ mu_2 \ right) x_2 $$

Vì f là quasiconvex,

$$ \ Rightarrow f \ left (u \ right) \ leq max \ left \ {f \ left (x_1 \ right), f \ left (z \ right) \ right \} = f \ left (z \ right) \ : \: và \: \: f \ left (v \ right) \ leq max \ left \ {f \ left (z \ right), f \ left (x_2 \ right) \ right \} $$

$$ \ Rightarrow f \ left (u \ right) \ leq f \ left (z \ right) \: \: và \: \: f \ left (v \ right) \ leq f \ left (z \ right) $ $

$$ \ Rightarrow max \ left \ {f \ left (u \ right), f \ left (v \ right) \ right \} \ leq f \ left (z \ right) $$

Nhưng z là điểm bất kỳ giữa u và v, nếu bất kỳ điểm nào trong số chúng bằng nhau thì f là hằng số.

Do đó, $ max \ left \ {f \ left (u \ right), f \ left (v \ right) \ right \} \ leq f \ left (z \ right) $

mâu thuẫn với độ chuẩn của f là $ z \ in \ left [u, v \ right] $.

Do đó f là hàm mặt lồi mạnh.

Định lý

Cho $ f: S \ rightarrow \ mathbb {R} ^ n $ và S là một tập lồi không rỗng trong $ \ mathbb {R} ^ n $. Nếu $ \ hat {x} $ là giải pháp tối ưu cục bộ thì $ \ hat {x} $ là giải pháp tối ưu toàn cục duy nhất.

Bằng chứng

Vì một hàm chuẩn tinh mạnh cũng là hàm chuẩn tinh, do đó giải pháp tối ưu cục bộ là giải pháp tối ưu toàn cục.

Uniqueness - Để f đạt được giải pháp tối ưu toàn cục tại hai điểm $ u, v \ in S $

$$ \ Rightarrow f \ left (u \ right) \ leq f \ left (x \ right). \ Forall x \ in S \: \: và \: \: f \ left (v \ right) \ leq f \ left (x \ right). \ forall x \ in S $$

Nếu u là giải pháp tối ưu chung, thì $ f \ left (u \ right) \ leq f \ left (v \ right) $ và $ f \ left (v \ right) \ leq f \ left (u \ right) \ Rightarrow f \ left (u \ right) = f \ left (v \ right) $

$$ f \ left (\ lambda u + \ left (1- \ lambda \ right) v \ right) <max \ left \ {f \ left (u \ right), f \ left (v \ right) \ right \} = f \ left (u \ right) $$

đó là một mâu thuẫn.

Do đó chỉ tồn tại một giải pháp tối ưu toàn cầu.

Nhận xét

• Một hàm chuẩn tinh mạnh cũng là một hàm chuẩn tinh hoàn toàn lồi.
• Một hàm lồi hoàn toàn có thể có hoặc có thể không là chuẩn tinh.
• Một phần lồi hoàn toàn có thể phân biệt được là một phần lồi mạnh.

Đặt $ f: S \ rightarrow \ mathbb {R} $ là một hàm phân biệt và S là một tập lồi không rỗng trong $ \ mathbb {R} ^ n $, thì f được cho là giả lồi nếu với mỗi $ x_1, x_2 \ in S $ với $ \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0 $, chúng ta có $ f \ left (x_2 \ right) \ geq f \ left ( x_1 \ right) $ hoặc tương đương nếu $ f \ left (x_1 \ right)> f \ left (x_2 \ right) $ thì $ \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right ) <0 $

Chức năng giả lõm

Đặt $ f: S \ rightarrow \ mathbb {R} $ là một hàm phân biệt và S là một tập lồi không rỗng trong $ \ mathbb {R} ^ n $, thì f được cho là giả lồi nếu với mỗi $ x_1, x_2 \ in S $ với $ \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0 $, chúng ta có $ f \ left (x_2 \ right) \ leq f \ left ( x_1 \ right) $ hoặc tương đương nếu $ f \ left (x_1 \ right)> f \ left (x_2 \ right) $ thì $ \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right )> 0 $

Nhận xét

• Nếu một hàm vừa giả lồi vừa giả lõm, thì được gọi là pseudolinear.

• Một hàm lồi có thể phân biệt được cũng là giả lồi.

• Một hàm giả lồi có thể không lồi. Ví dụ,

  $ f \ left (x \ right) = x + x ^ 3 $ không lồi. Nếu $ x_1 \ leq x_2, x_ {1} ^ {3} \ leq x_ {2} ^ {3} $

  Do đó, $ \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) = \ left (1 + 3x_ {1} ^ {2} \ right) \ left (x_2-x_1 \ right) \ geq 0 $

  Và, $ f \ left (x_2 \ right) -f \ left (x_1 \ right) = \ left (x_2-x_1 \ right) + \ left (x_ {2} ^ {3} -x_ {1} ^ {3 } \ right) \ geq 0 $

  $ \ Rightarrow f \ left (x_2 \ right) \ geq f \ left (x_1 \ right) $

  Vì vậy, nó là giả lồi.

  Một hàm giả lồi là một hàm gần như hoàn toàn lồi. Do đó, mọi cực tiểu cục bộ của giả lồi cũng là cực tiểu toàn cục.

Hàm giả lồi chính xác

Đặt $ f: S \ rightarrow \ mathbb {R} $ là một hàm phân biệt và S là một tập lồi không rỗng trong $ \ mathbb {R} ^ n $, thì f được cho là giả lồi nếu với mỗi $ x_1, x_2 \ in S $ với $ \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right) \ geq 0 $, chúng ta có $ f \ left (x_2 \ right)> f \ left (x_1 \ right) $ hoặc tương đương nếu $ f \ left (x_1 \ right) \ geq f \ left (x_2 \ right) $ then $ \ bigtriangledown f \ left (x_1 \ right) ^ T \ left (x_2-x_1 \ right ) <0 $

Định lý

Gọi f là một hàm giả lồi và giả sử $ \ bigtriangledown f \ left (\ hat {x} \ right) = 0 $ cho một số $ \ hat {x} \ trong S $, thì $ \ hat {x} $ là tối ưu toàn cục nghiệm của f trên S.

Bằng chứng

Gọi $ \ hat {x} $ là điểm tới hạn của f, tức là $ \ bigtriangledown f \ left (\ hat {x} \ right) = 0 $

Vì f là hàm giả lồi nên đối với $ x \ in S, $ chúng ta có

$$ \ bigtriangledown f \ left (\ hat {x} \ right) \ left (x- \ hat {x} \ right) = 0 \ Rightarrow f \ left (\ hat {x} \ right) \ leq f \ left (x \ right), \ forall x \ in S $$

Do đó, $ \ hat {x} $ là giải pháp tối ưu toàn cầu.

Nhận xét

Nếu f là hàm giả lồi hoàn toàn, thì $ \ hat {x} $ là giải pháp tối ưu toàn cục duy nhất.

Định lý

Nếu f là hàm giả lồi có thể phân biệt được so với S, thì f vừa là hàm chuẩn gần vừa là hàm chuẩn.

Nhận xét

• Tổng của hai cầu lồi được xác định trên tập hợp mở S của $ \ mathbb {R} ^ n $ có thể không phải là giả lồi.

• Đặt $ f: S \ rightarrow \ mathbb {R} $ là một hàm mặt lồi và S là một tập con lồi khác rỗng của $ \ mathbb {R} ^ n $ thì f là giả lồi nếu và chỉ khi mọi điểm tới hạn là một tổng thể cực tiểu của f trên S.

• Gọi S là một tập con lồi khác rỗng của $ \ mathbb {R} ^ n $ và $ f: S \ rightarrow \ mathbb {R} $ là một hàm sao cho $ \ bigtriangledown f \ left (x \ right) \ neq 0 $ với mọi $ x \ trong S $ thì f là giả lồi nếu và chỉ khi nó là một hàm chuẩn lồi.

Có bốn dạng bài toán lập trình lồi -

Step 1 - $ min \: f \ left (x \ right) $, trong đó $ x \ in S $ và S là một tập lồi không rỗng trong $ \ mathbb {R} ^ n $ và $ f \ left (x \ right ) $ là hàm lồi.

Step 2 - $ min \: f \ left (x \ right), x \ in \ mathbb {R} ^ n $ theo chủ đề

$ g_i \ left (x \ right) \ geq 0, 1 \ leq m_1 $ và $ g_i \ left (x \ right) $ là một hàm lồi.

$ g_i \ left (x \ right) \ leq 0, m_1 + 1 \ leq m_2 $ và $ g_i \ left (x \ right) $ là một hàm lõm.

$ g_i \ left (x \ right) = 0, m_2 + 1 \ leq m $ và $ g_i \ left (x \ right) $ là một hàm tuyến tính.

trong đó $ f \ left (x \ right) $ là một fucntion lồi.

Step 3 - $ max \: f \ left (x \ right) $ trong đó $ x \ in S $ và S là một tập lồi không rỗng trong $ \ mathbb {R} ^ n $ và $ f \ left (x \ right) $ là hàm lõm.

Step 4 - $ min \: f \ left (x \ right) $, trong đó $ x \ in \ mathbb {R} ^ n $ chủ đề

$ g_i \ left (x \ right) \ geq 0, 1 \ leq m_1 $ và $ g_i \ left (x \ right) $ là một hàm lồi.

$ g_i \ left (x \ right) \ leq 0, m_1 + 1 \ leq m_2 $ và $ g_i \ left (x \ right) $ là một hàm lõm.

$ g_i \ left (x \ right) = 0, m_2 + 1 \ leq m $ và $ g_i \ left (x \ right) $ là một hàm tuyến tính.

trong đó $ f \ left (x \ right) $ là một hàm lõm.

Hình nón của hướng khả thi

Gọi S là một tập khác rỗng trong $ \ mathbb {R} ^ n $ và đặt $ \ hat {x} \ in \: Closure \ left (S \ right) $, khi đó hình nón có hướng khả thi của S là $ \ hat {x} $, ký hiệu là D, được định nghĩa là $ D = \ left \ {d: d \ neq 0, \ hat {x} + \ lambda d \ in S, \ lambda \ in \ left (0, \ delta \ right), \ delta> 0 \ right \} $

Mỗi vectơ khác 0 $ d \ trong D $ được gọi là hướng khả thi.

Đối với một hàm đã cho $ f: \ mathbb {R} ^ n \ Rightarrow \ mathbb {R} $, hình nón có hướng cải thiện tại $ \ hat {x} $ được ký hiệu là F và được cho bởi

$$ F = \ left \ {d: f \ left (\ hat {x} + \ lambda d \ right) \ leq f \ left (\ hat {x} \ right), \ forall \ lambda \ in \ left ( 0, \ delta \ right), \ delta> 0 \ right \} $$

Mỗi hướng $ d \ trong F $ được gọi là hướng đi lên hoặc hướng đi xuống của f tại $ \ hat {x} $

Định lý

Necessary Condition

Xét bài toán $ min f \ left (x \ right) $ sao cho $ x \ in S $ trong đó S là một tập khác rỗng trong $ \ mathbb {R} ^ n $. Giả sử f có thể phân biệt được tại một điểm $ \ hat {x} \ trong S $. Nếu $ \ hat {x} $ là một giải pháp tối ưu cục bộ thì $ F_0 \ cap D = \ phi $ trong đó $ F_0 = \ left \ {d: \ bigtriangledown f \ left (\ hat {x} \ right) ^ T d <0 \ right \} $ và D là một hình nón có hướng khả thi.

Sufficient Condition

Nếu $ F_0 \ cap D = \ phi $ f là một hàm giả lồi tại $ \ hat {x} $ và tồn tại một vùng lân cận của $ \ hat {x}, N_ \ varepsilon \ left (\ hat {x} \ right) , \ varepsilon> 0 $ sao cho $ d = x- \ hat {x} \ in D $ cho $ x \ in S \ cap N_ \ varepsilon \ left (\ hat {x} \ right) $ bất kỳ, sau đó $ \ hat {x} $ là giải pháp tối ưu cục bộ.

Bằng chứng

Necessary Condition

Cho $ F_0 \ cap D \ neq \ phi $, tức là tồn tại một $ d \ in F_0 \ cap D $ sao cho $ d \ in F_0 $ và $ d \ in D $

Vì $ d \ in D $, nên tồn tại $ \ delta_1> 0 $ sao cho $ \ hat {x} + \ lambda d \ in S, \ lambda \ in \ left (0, \ delta_1 \ right). $

Vì $ d \ in F_0 $, do đó $ \ bigtriangledown f \ left (\ hat {x} \ right) ^ T d <0 $

Do đó, tồn tại $ \ delta_2> 0 $ sao cho $ f \ left (\ hat {x} + \ lambda d \ right) <f \ left (\ hat {x} \ right), \ forall \ lambda \ in f \ left (0, \ delta_2 \ right) $

Hãy để $ \ delta = min \ left \ {\ delta_1, \ delta_2 \ right \} $

Sau đó $ \ hat {x} + \ lambda d \ in S, f \ left (\ hat {x} + \ lambda d \ right) <f \ left (\ hat {x} \ right), \ forall \ lambda \ ở f \ left (0, \ delta \ right) $

Nhưng $ \ hat {x} $ là giải pháp tối ưu cục bộ.

Do đó nó là mâu thuẫn.

Do đó $ F_0 \ cap D = \ phi $

Sufficient Condition

Đặt $ F_0 \ cap D \ neq \ phi $ nd cho f là một hàm giả lồi.

Giả sử tồn tại một vùng lân cận của $ \ hat {x}, N _ {\ varepsilon} \ left (\ hat {x} \ right) $ sao cho $ d = x- \ hat {x}, \ forall x \ in S \ mũ N_ \ varepsilon \ left (\ hat {x} \ phải) $

Cho rằng $ \ hat {x} $ không phải là giải pháp tối ưu cục bộ.

Do đó, tồn tại $ \ bar {x} \ trong S \ cap N_ \ varepsilon \ left (\ hat {x} \ right) $ sao cho $ f \ left (\ bar {x} \ right) <f \ left ( \ hat {x} \ right) $

Theo giả định trên $ S \ cap N_ \ varepsilon \ left (\ hat {x} \ right), d = \ left (\ bar {x} - \ hat {x} \ right) \ trong D $

Bằng giả lồi của f,

$$ f \ left (\ hat {x} \ right)> f \ left (\ bar {x} \ right) \ Rightarrow \ bigtriangledown f \ left (\ hat {x} \ right) ^ T \ left (\ bar {x} - \ hat {x} \ right) <0 $$

$ \ Rightarrow \ bigtriangledown f \ left (\ hat {x} \ right) ^ T d <0 $

$ \ Rightarrow d \ in F_0 $

do đó $ F_0 \ cap D \ neq \ phi $

đó là một mâu thuẫn.

Do đó, $ \ hat {x} $ là giải pháp tối ưu cục bộ.

Hãy xem xét vấn đề sau: $ min \: f \ left (x \ right) $ trong đó $ x \ in X $ sao cho $ g_x \ left (x \ right) \ leq 0, i = 1,2, ..., m $

$ f: X \ rightarrow \ mathbb {R}, g_i: X \ rightarrow \ mathbb {R} ^ n $ và X là một tập hợp mở trong $ \ mathbb {R} ^ n $

Cho $ S = \ left \ {x: g_i \ left (x \ right) \ leq 0, \ forall i \ right \} $

Đặt $ \ hat {x} \ trong X $, sau đó $ M = \ left \ {1,2, ..., m \ right \} $

Đặt $ I = \ left \ {i: g_i \ left (\ hat {x} \ right) = 0, i \ in M ​​\ right \} $ nơi tôi được gọi là bộ chỉ mục cho tất cả các ràng buộc hoạt động tại $ \ hat {x } $

Đặt $ J = \ left \ {i: g_i \ left (\ hat {x} \ right) <0, i \ in M ​​\ right \} $ trong đó J được gọi là bộ chỉ mục cho tất cả các ràng buộc hoạt động tại $ \ hat {x } $.

Cho $ F_0 = \ left \ {d \ in \ mathbb {R} ^ m: \ bigtriangledown f \ left (\ hat {x} \ right) ^ T d <0 \ right \} $

Cho $ G_0 = \ left \ {d \ in \ mathbb {R} ^ m: \ bigtriangledown gI \ left (\ hat {x} \ right) ^ T d <0 \ right \} $

hoặc $ G_0 = \ left \ {d \ in \ mathbb {R} ^ m: \ bigtriangledown gi \ left (\ hat {x} \ right) ^ T d <0, \ forall i \ in I \ right \} $

Bổ đề

Nếu $ S = \ left \ {x \ in X: g_i \ left (x \ right) \ leq 0, \ forall i \ in I \ right \} $ và X là tập mở không trống trong $ \ mathbb {R } ^ n $. Đặt $ \ hat {x} \ in S $ và $ g_i $ khác nhau ở $ \ hat {x}, i \ in I $ và để $ g_i $ trong đó $ i \ in J $ liên tục ở $ \ hat {x } $, rồi đến $ G_0 \ subseteq D $.

Bằng chứng

Cho $ d \ trong G_0 $

Vì $ \ hat {x} \ in X $ và X là một tập hợp mở, do đó, tồn tại $ \ delta_1> 0 $ sao cho $ \ hat {x} + \ lambda d \ in X $ cho $ \ lambda \ in \ trái (0, \ delta_1 \ phải) $

Ngoài ra, vì $ g_ \ hat {x} <0 $ và $ g_i $ liên tục ở $ \ hat {x}, \ forall i \ in J $, nên tồn tại $ \ delta_2> 0 $, $ g_i \ left (\ hat {x} + \ lambda d \ right) <0, \ lambda \ in \ left (0, \ delta_2 \ right) $

Vì $ d \ in G_0 $ nên $ \ bigtriangledown g_i \ left (\ hat {x} \ right) ^ T d <0, \ forall i \ in I $ nên tồn tại $ \ delta_3> 0, g_i \ left (\ hat {x} + \ lambda d \ right) <g_i \ left (\ hat {x} \ right) = 0 $, cho $ \ lambda \ in \ left (0, \ delta_3 \ right) i \ in J $

Để $ \ delta = min \ left \ {\ delta_1, \ delta_2, \ delta_3 \ right \} $

do đó, $ \ hat {x} + \ lambda d \ in X, g_i \ left (\ hat {x} + \ lambda d \ right) <0, i \ in M ​​$

$ \ Rightarrow \ hat {x} + \ lambda d \ in S $

$ \ Rightarrow d \ in D $

$ \ Rightarrow G_0 \ subseteq D $

Do đó đã được chứng minh.

Định lý

Necessary Condition

Giả sử $ f $ và $ g_i, i \ in I $, khác với $ \ hat {x} \ in S, $ và $ g_j $ liên tục với $ \ hat {x} \ trong S $. Nếu $ \ hat {x} $ là cực tiểu cục bộ của $ S $ thì $ F_0 \ cap G_0 = \ phi $.

Sufficient Condition

Nếu $ F_0 \ cap G_0 = \ phi $ và f là hàm giả lồi ở $ \ left (\ hat {x}, g_i 9x \ right), thì i \ in I $ là hàm giả lồi trên một số $ \ varepsilon $ - vùng lân cận của $ \ hat {x}, \ hat {x} $ là giải pháp tối ưu cục bộ.

Nhận xét

• Đặt $ \ hat {x} $ là một điểm khả thi sao cho $ \ bigtriangledown f \ left (\ hat {x} \ right) = 0 $, thì $ F_0 = \ phi $. Do đó, $ F_0 \ cap G_0 = \ phi $ nhưng $ \ hat {x} $ không phải là giải pháp tối ưu

• Nhưng nếu $ \ bigtriangledown g \ left (\ hat {x} \ right) = 0 $ thì $ G_0 = \ phi $, do đó $ F_0 \ cap G_0 = \ phi $

• Xem xét vấn đề: min $ f \ left (x \ right) $ sao cho $ g \ left (x \ right) = 0 $.

  Vì $ g \ left (x \ right) = 0 $ nên $ g_1 \ left (x \ right) = g \ left (x \ right) <0 $ và $ g_2 \ left (x \ right) = - g \ left (x \ right) \ leq 0 $.

  Đặt $ \ hat {x} \ bằng S $, sau đó $ g_1 \ left (\ hat {x} \ right) = 0 $ và $ g_2 \ left (\ hat {x} \ right) = 0 $.

  Nhưng $ \ bigtriangledown g_1 \ left (\ hat {x} \ right) = - \ bigtriangledown g_2 \ left (\ hat {x} \ right) $

  Do đó, $ G_0 = \ phi $ và $ F_0 \ cap G_0 = \ phi $.

Điều kiện cần thiết

Định lý

Xem xét vấn đề - $ min f \ left (x \ right) $ sao cho $ x \ in X $ trong đó X là một tập hợp mở trong $ \ mathbb {R} ^ n $ và đặt $ g_i \ left (x \ right) \ leq 0, \ forall i = 1,2, .... m $.

Cho $ f: X \ rightarrow \ mathbb {R} $ và $ g_i: X \ rightarrow \ mathbb {R} $

Hãy để $ \ hat {x} $ là một giải pháp khả thi và để cho f và $ g_i, i \ in I $ là phân biệt ở $ \ hat {x} $ và $ g_i, i \ in J $ liên tục ở $ \ hat { x} $.

Nếu $ \ hat {x} $ giải quyết cục bộ vấn đề trên thì tồn tại $ u_0, u_i \ in \ mathbb {R}, i \ in I $ sao cho $ u_0 \ bigtriangledown f \ left (\ hat {x} \ phải) + \ displaystyle \ sum \ limit_ {i \ in I} u_i \ bigtriangledown g_i \ left (\ hat {x} \ right) $ = 0

trong đó $ u_0, u_i \ geq 0, i \ in I $ và $ \ left (u_0, u_I \ right) \ neq \ left (0,0 \ right) $

Hơn nữa, nếu $ g_i, i \ in J $ cũng có thể phân biệt được ở $ \ hat {x} $, thì các điều kiện trên có thể được viết là:

$ u_0 \ bigtriangledown f \ left (\ hat {x} \ right) + \ displaystyle \ sum \ limit_ {i = 1} ^ m u_i \ bigtriangledown g_i \ left (\ hat {x} \ right) = 0 $

$ u_ig_i \ left (\ hat {x} \ right) $ = 0

$ u_0, u_i \ geq 0, \ forall i = 1,2, ...., m $

$ \ left (u_0, u \ right) \ neq \ left (0,0 \ right), u = \ left (u_1, u_2, s, u_m \ right) \ in \ mathbb {R} ^ m $

Nhận xét

• $ u_i $ được gọi là số nhân Lagrangian.

• Điều kiện $ \ hat {x} $ khả thi cho bài toán đã cho được gọi là điều kiện khả thi ban đầu.

• Yêu cầu $ u_0 \ bigtriangledown f \ left (\ hat {x} \ right) + \ displaystyle \ sum \ limit_ {i = 1} ^ m ui \ bigtriangledown g_i \ left (x \ right) = 0 $ được gọi là tính khả thi kép tình trạng.

• Điều kiện $ u_ig_i \ left (\ hat {x} \ right) = 0, i = 1, 2, ... m $ được gọi là điều kiện độ chùng bổ sung. Điều kiện này yêu cầu $ u_i = 0, i \ in J $

• Cùng với điều kiện khả thi ban đầu, điều kiện khả thi kép và độ trễ bổ sung được gọi là Điều kiện Fritz-John.

Điều kiện đủ

Định lý

Nếu tồn tại $ \ varepsilon $ -neighbourhood $ \ hat {x} N_ \ varepsilon \ left (\ hat {x} \ right), \ varepsilon> 0 $ sao cho f là giả lồi trên $ N_ \ varepsilon \ left ( \ hat {x} \ right) \ cap S $ và $ g_i, i \ in I $ hoàn toàn là lồi giả trên $ N_ \ varepsilon \ left (\ hat {x} \ right) \ cap S $, rồi $ \ hat { x} $ là giải pháp tối ưu cục bộ cho vấn đề được mô tả ở trên. Nếu f là giả lồi tại $ \ hat {x} $ và nếu $ g_i, i \ in I $ đều là hàm giả lồi và chuẩn thực tại $ \ hat {x}, \ hat {x} $ là giải pháp tối ưu toàn cục cho vấn đề miêu tả trên.

Thí dụ

• $ min \: f \ left (x_1, x_2 \ right) = \ left (x_1-3 \ right) ^ 2 + \ left (x_2-2 \ right) ^ 2 $

  sao cho $ x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 5, x_1 + 2x_2 \ leq 4, x_1, x_2 \ geq 0 $ Và $ \ hat {x} = \ left (2 , 1 \ phải) $

  Cho $ g_1 \ left (x_1, x_2 \ right) = x_ {1} ^ {2} + x_ {2} ^ {2} -5, $

  $ g_2 \ left (x_1, x_2 \ right) = x_1 + 2x_2-4, $

  $ g_3 \ left (x_1, x_2 \ right) = - x_1 $ và $ g_4 \ left (x_1, x_2 \ right) = -x_2 $.

  Do đó, các ràng buộc trên có thể được viết là:

  $ g_1 \ left (x_1, x_2 \ right) \ leq 0, $

  $ g_2 \ left (x_1, x_2 \ right) \ leq 0, $

  $ g_3 \ left (x_1, x_2 \ right) \ leq 0 $ và

  $ g_4 \ left (x_1, x_2 \ right) \ leq 0 $ Do đó, $ I = \ left \ {1,2 \ right \} $, do đó, $ u_3 = 0, u_4 = 0 $

  $ \ bigtriangledown f \ left (\ hat {x} \ right) = \ left (2, -2 \ right), \ bigtriangledown g_1 \ left (\ hat {x} \ right) = \ left (4,2 \ right ) $ và $ \ bigtriangledown g_2 \ left (\ hat {x} \ right) = \ left (1,2 \ right) $

  Do đó, đặt các giá trị này trong điều kiện đầu tiên của điều kiện Fritz-John, chúng ta nhận được -

  $ u_0 = \ frac {3} {2} u_2, \: \: u_1 = \ frac {1} {2} u_2, $ và đặt $ u_2 = 1 $, do đó $ u_0 = \ frac {3} {2} , \: \: u_1 = \ frac {1} {2} $

  Như vậy điều kiện Fritz John được thỏa mãn.

• $ min f \ left (x_1, x_2 \ right) = - x_1 $.

  sao cho $ x_2- \ left (1-x_1 \ right) ^ 3 \ leq 0 $,

  $ -x_2 \ leq 0 $ và $ \ hat {x} = \ left (1,0 \ right) $

  Cho $ g_1 \ left (x_1, x_2 \ right) = x_2- \ left (1-x_1 \ right) ^ 3 $,

  $ g_2 \ left (x_1, x_2 \ right) = - x_2 $

  Do đó, các ràng buộc trên có thể được viết thành:

  $ g_1 \ left (x_1, x_2 \ right) \ leq 0, $

  $ g_2 \ left (x_1, x_2 \ right) \ leq 0, $

  Do đó, $ I = \ left \ {1,2 \ right \} $

  $ \ bigtriangledown f \ left (\ hat {x} \ right) = \ left (-1,0 \ right) $

  $ \ bigtriangledown g_1 \ left (\ hat {x} \ right) = \ left (0,1 \ right) $ và $ g_2 \ left (\ hat {x} \ right) = \ left (0, -1 \ right ) $

  Do đó, đặt các giá trị này trong điều kiện đầu tiên của điều kiện Fritz-John, chúng ta nhận được -

  $ u_0 = 0, \: \: u_1 = u_2 = a> 0 $

  Như vậy điều kiện Fritz John được thỏa mãn.

Xem xét vấn đề -

$ min \: f \ left (x \ right) $ sao cho $ x \ in X $, trong đó X là tập hợp mở trong $ \ mathbb {R} ^ n $ và $ g_i \ left (x \ right) \ leq 0, i = 1, 2, ..., m $

Cho $ S = \ left \ {x \ trong X: g_i \ left (x \ right) \ leq 0, \ forall i \ right \} $

Giả sử $ \ hat {x} \ trong S $ và cho $ f $ và $ g_i, i \ in I $ có thể phân biệt được ở $ \ hat {x} $ và $ g_i, i \ trong J $ liên tục ở $ \ hat {x} $. Hơn nữa, $ \ bigtriangledown g_i \ left (\ hat {x} \ right), i \ in I $ độc lập tuyến tính. Nếu $ \ hat {x} $ giải quyết cục bộ vấn đề trên, thì có $ u_i, i \ in I $ sao cho

$ \ bigtriangledown f \ left (x \ right) + \ displaystyle \ sum \ limit_ {i \ in I} u_i \ bigtriangledown g_i \ left (\ hat {x} \ right) = 0 $, $ \: \: u_i \ geq 0, tôi trong I $

Nếu $ g_i, i \ in J $ cũng có thể phân biệt được ở $ \ hat {x} $. sau đó $ \ hat {x} $, sau đó

$ \ bigtriangledown f \ left (\ hat {x} \ right) + \ displaystyle \ sum \ limit_ {i = 1} ^ m u_i \ bigtriangledown g_i \ left (\ hat {x} \ right) = 0 $

$ u_ig_i \ left (\ hat {x} \ right) = 0, \ forall i = 1,2, ..., m $

$ u_i \ geq 0 \ forall i = 1,2, ..., m $

Thí dụ

Hãy xem xét vấn đề sau -

$ min \: f \ left (x_1, x_2 \ right) = \ left (x_1-3 \ right) ^ 2 + \ left (x_2-2 \ right) ^ 2 $

sao cho $ x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 5 $,

$ x_1,2x_2 \ geq 0 $ và $ \ hat {x} = \ left (2,1 \ right) $

Cho $ g_1 \ left (x_1, x_2 \ right) = x_ {1} ^ {2} + x_ {2} ^ {2} -5 $,

$ g_2 \ left (x_1, x_2 \ right) = x_ {1} + 2x_2-4 $

$ g_3 \ left (x_1, x_2 \ right) = - x_ {1} $ và $ g_4 \ left (x_1, x_2 \ right) = - x_2 $

Do đó, các ràng buộc trên có thể được viết là:

$ g_1 \ left (x_1, x_2 \ right) \ leq 0, g_2 \ left (x_1, x_2 \ right) \ leq 0 $

$ g_3 \ left (x_1, x_2 \ right) \ leq 0, $ và $ g_4 \ left (x_1, x_2 \ right) \ leq 0 $ Do đó, $ I = \ left \ {1,2 \ right \} $ , $ u_3 = 0, \: \: u_4 = 0 $

$ \ bigtriangledown f \ left (\ hat {x} \ right) = \ left (2, -2 \ right), \ bigtriangledown g_1 \ left (\ hat {x} \ right) = \ left (4,2 \ right ) $ và

$ \ bigtriangledown g_2 \ left (\ hat {x} \ right) = \ left (1,2 \ right) $

Do đó, đặt các giá trị này trong điều kiện đầu tiên của điều kiện Karush-Kuhn-Tucker, chúng tôi nhận được -

$ u_1 = \ frac {1} {3} $ và $ u_2 = \ frac {2} {3} $

Như vậy điều kiện Karush-Kuhn-Tucker được thỏa mãn.

Phương pháp xuống dốc nhất

Phương pháp này còn được gọi là phương pháp Gradient hoặc phương pháp Cauchy. Phương pháp này liên quan đến các thuật ngữ sau:

$$ x_ {k + 1} = x_k + \ alpha_kd_k $$

$ d_k = - \ bigtriangledown f \ left (x_k \ right) $ hoặc $ d_k = - \ frac {\ bigtriangledown f \ left (x_k \ right)} {\ left \ | \ bigtriangledown f \ left (x_k \ right) \ right \ |} $

Cho $ \ phi \ left (\ alpha \ right) = f \ left (x_k + \ alpha d_k \ right) $

Bằng cách phân biệt $ \ phi $ và cân bằng nó với 0, chúng ta có thể nhận được $ \ alpha $.

Vì vậy, thuật toán diễn ra như sau:

• Khởi tạo $ x_0 $, $ \ varepsilon_1 $, $ \ varepsilon_2 $ và đặt $ k = 0 $.

• Đặt $ d_k = - \ bigtriangledown f \ left (x_k \ right) $ hoặc $ d_k = - \ frac {\ bigtriangledown f \ left (x_k \ right)} {\ left \ | \ bigtriangledown f \ left (x_k \ right) \ right \ |} $.

• tìm $ \ alpha_k $ sao cho nó thu nhỏ $ \ phi \ left (\ alpha \ right) = f \ left (x_k + \ alpha d_k \ right) $.

• Đặt $ x_ {k + 1} = x_k + \ alpha_kd_k $.

• Nếu $ \ left \ | x_ {k + 1-x_k} \ right \ | <\ varepsilon_1 $ hoặc $ \ left \ | \ bigtriangledown f \ left (x_ {k + 1} \ right) \ right \ | \ leq \ varepsilon_2 $, chuyển sang bước 6, nếu không thì đặt $ k = k + 1 $ và chuyển sang bước 2.

• Giải pháp tối ưu là $ \ hat {x} = x_ {k + 1} $.

Phương pháp Newton

Phương pháp Newton hoạt động dựa trên nguyên tắc sau:

$ f \ left (x \ right) = y \ left (x \ right) = f \ left (x_k \ right) + \ left (x-x_k \ right) ^ T \ bigtriangledown f \ left (x_k \ right) + \ frac {1} {2} \ left (x-x_k \ right) ^ TH \ left (x_k \ right) \ left (x-x_k \ right) $

$ \ bigtriangledown y \ left (x \ right) = \ bigtriangledown f \ left (x_k \ right) + H \ left (x_k \ right) \ left (x-x_k \ right) $

Tại $ x_ {k + 1}, \ bigtriangledown y \ left (x_ {k + 1} \ right) = \ bigtriangledown f \ left (x_k \ right) + H \ left (x_k \ right) \ left (x_ {k +1} -x_k \ right) $

Để $ x_ {k + 1} $ là giải pháp tối ưu thì $ \ bigtriangledown y \ left (x_k + 1 \ right) = 0 $

Do đó, $ x_ {k + 1} = x_k-H \ left (x_k \ right) ^ {- 1} \ bigtriangledown f \ left (x_k \ right) $

Ở đây $ H \ left (x_k \ right) $ không phải là số ít.

Do đó thuật toán diễn ra như sau:

Step 1 - Khởi tạo $ x_0, \ varepsilon $ và đặt $ k = 0 $.

Step 2 - tìm $ H \ left (x_k \ right) \ bigtriangledown f \ left (x_k \ right) $.

Step 3 - Giải hệ tuyến tính $ H \ left (x_k \ right) h \ left (x_k \ right) = \ bigtriangledown f \ left (x_k \ right) $ cho $ h \ left (x_k \ right) $.

Step 4 - tìm $ x_ {k + 1} = x_k-h \ left (x_k \ right) $.

Step 5- Nếu $ \ left \ | x_ {k + 1} -x_k \ right \ | <\ varepsilon $ hoặc $ \ left \ | \ bigtriangledown f \ left (x_k \ right) \ right \ | \ leq \ varepsilon $ sau đó chuyển sang bước 6, nếu không thì đặt $ k = k + 1 $ và chuyển sang bước 2.

Step 6 - Giải pháp tối ưu là $ \ hat {x} = x_ {k + 1} $.

Phương pháp Gradient Liên hợp

Phương pháp này được sử dụng để giải các bài toán thuộc các dạng sau:

$ min f \ left (x \ right) = \ frac {1} {2} x ^ T Qx-bx $

trong đó Q là ma trận nXn xác định dương và b là hằng số.

Cho $ x_0, \ varepsilon, $ compute $ g_0 = Qx_0-b $

Đặt $ d_0 = -g_0 $ cho $ k = 0,1,2, ..., $

Đặt $ \ alpha_k = \ frac {g_ {k} ^ {T} g_k} {d_ {k} ^ {T} Q d_k} $

Tính $ x_ {k + 1} = x_k + \ alpha_kd_k $

Đặt $ g_ {k + 1} = g_k + \ alpha_kd_k $

Tính $ \ beta_k = \ frac {g_ {k} ^ {T} g_k} {d_ {k} ^ {T} Qd_k} $

Tính $ x_ {k + 1} = x_k + \ alpha_kd_k $

Đặt $ g_ {k + 1} = x_k + \ alpha_kQd_k $

Tính $ \ beta_k = \ frac {g_ {k + 1} ^ {T} g_ {k + 1}} {g_ {k} ^ {T} gk} $

Đặt $ d_ {k + 1} = - g_ {k + 1} + \ beta_kd_k $.