Eignung - Geometrie

Punkt

Ein Punkt ist ein genauer Ort

Liniensegment

Der gerade Weg zwischen zwei Punkten A und B wird als Liniensegment AB bezeichnet. Ein Liniensegment hat zwei Endpunkte.

Strahl

Wenn wir ein Liniensegment AB auf unbestimmte Zeit in eine Richtung verlängern, erhalten wir den Strahl AB. Ray AB hat einen Endpunkt, nämlich A.

LINIE

Ein in beide Richtungen unbegrenzt ausgedehntes Liniensegment AB wird als Linie AB bezeichnet.

Eine Linie enthält unendlich viele Punkte.
Durch gegebene Punkte können unendlich viele Linien gezogen werden.
Es kann nur eine Linie gezogen werden, um durch zwei gegebene Punkte A und B zu verlaufen.
Zwei Linien treffen sich in einem Punkt.
Zwei Flugzeuge treffen sich in einer Reihe.

Kollinear

In der angegebenen Figur sind die Punkte A, B, C kollinear.

Gleichzeitige Linien

Drei oder mehr Linien, die sich an denselben Punkten schneiden, werden als gleichzeitige Linien bezeichnet.

Winkel

Zwei Strahlen OA und OB mit gemeinsamen Endpunkten O bilden den Winkel AOB, geschrieben als ∠AOB

Winkelmaß

Das Ausmaß der Drehung von OA nach OB wird als Maß für ∠AOB bezeichnet, geschrieben als m (∠AOB).

Ein Winkel von 360 °

Wenn sich ein Strahl OA ausgehend von seiner ursprünglichen Position OA gegen den Uhrzeigersinn um O dreht und nach einer vollständigen Drehung wieder in seine ursprüngliche Position zurückkehrt, sagen wir, dass er sich um 360 gedreht hat. Diese vollständige Drehung ist in 360 ° gleiche Teile unterteilt. Dann heißt jeder Teil 1 Grad, geschrieben als 1 °

1 ° = 60 Minuten, geschrieben als 60 '

1 Minute = 60 Sekunden, geschrieben als 60 "

Arten von Winkeln

Right angle - Ein Winkel mit einem Maß von 90 ° wird als rechter Winkel bezeichnet.
Acute angle - Ein Winkel, dessen Maß weniger als 90 ° beträgt, wird als spitzer Winkel bezeichnet.
Obtuse angle - Ein Winkel, dessen Maß mehr als 90 °, aber weniger als 180 ° beträgt, wird als stumpfer Winkel bezeichnet.
Straight angle - Ein Winkel mit einem Maß von 180 ° wird als gerader Winkel bezeichnet.
Reflex angle - Ein Winkel, dessen Maß mehr als 180 °, aber weniger als 360 ° beträgt, wird als Reflexwinkel bezeichnet.
Complete angle - Ein Winkel, dessen Maß 360 ° beträgt, wird als vollständiger Winkel bezeichnet.
Equal angle - Zwei Winkel gelten als gleich, wenn sie das gleiche Maß haben.
Complementary angleZwei Winkel werden als komplementär bezeichnet, wenn die Summe ihrer Maße 90 beträgt. Beispielsweise sind Winkel von 65 ° und 25 ° komplementäre Winkel.
Supplementary angle- Zwei Winkel gelten als ergänzend, wenn die Summe ihrer Maße 180 ° beträgt. Beispielsweise sind Winkelmaße von 70 ° und 110 ° ergänzend.
Adjacent angle- Zwei Winkel werden als benachbarter Winkel bezeichnet, wenn sie denselben Scheitelpunkt und einen gemeinsamen Arm haben, so dass sich nicht gemeinsame Arme auf beiden Seiten des Kommanarms befinden. In der angegebenen Abbildung sind ∠AOC und ∠BOC benachbarte Winkel.

Wichtige Ergebnisse

Wenn ein Strahl auf einer Linie steht, beträgt die Summe zweier so gebildeter benachbarter Winkel 180 °. In der angegebenen Abbildung steht der Strahl CP auf der Linie AB.

∴ ∠ACD + ∠BCD = 180°.

Die Summe aller Winkel, die an einem bestimmten Punkt der Linie auf derselben Seite einer Linie gebildet werden, beträgt 180 °. In der angegebenen Abbildung sind vier Winkel auf derselben Seite von AOB gebildet.

∴ ∠AOE + ∠EOD + ∠DOC + ∠COD = 180°.

Die Summe aller Winkel um einen Punkt beträgt 360 °. In der angegebenen Abbildung werden fünf Winkel um einen Punkt O gebildet.

∴∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA=360°.

Vertikal gegenüberliegende Winkel

Wenn sich zwei Linien A Band CD an einem Punkt O schneiden, sind AOC, BOD und BOC, AOD zwei Paare von vertikal entgegengesetzten Winkeln. Vertikal entgegengesetzte Winkel sind immer gleich.

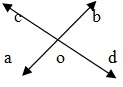
∴ ∠AOC = ∠BOD and ∠AOD = ∠BOC

Parallele Linien

Wenn zwei Linien in derselben Ebene liegen und sich nicht schneiden, wenn sie auf beiden Seiten erzeugt werden, werden solche Linien als parallel bezeichnet und wir schreiben L || m.

Querlinie, die parallele Linien schneidet

Es seien zwei parallele Linien AB und CD durch eine transversale EF geschnitten. Dann

Entsprechender Winkel sind gleich

(∠1 = ∠5), (∠4= ∠8 ), (∠2 = ∠6) , (∠3 = ∠7)

Alternative Innenwinkel sind gleich.

(∠3 =∠5 )  and  (∠4 =∠6 )

Konsakte Innenwinkel sind ergänzend

∠4+∠5 = 180° and ∠3 +∠6 = 180°.

Dreieck

Eine durch drei gerade Linien begrenzte Figur wird als Dreieck bezeichnet. In der angegebenen Abbildung haben wir ∆ABC; ∆ABC mit drei Eckpunkten A, B, C. In hat drei Winkel, nämlich ∠A, ∠B und ∠C. Es hat drei Seiten, nämlich AB, AC und BC.

Arten von Dreiecken

Ein Dreieck mit allen Seiten ist gleichseitiges Dreieck.
Ein Dreieck mit zwei gleichen Seiten wird als gleichschenkliges Dreieck bezeichnet.
Ein Dreieck mit allen Seiten unterschiedlicher Länge wird als Skalenendreieck bezeichnet.
Ein Dreieck, dessen Winkel 90 ° beträgt, wird als rechtwinkliges Dreieck bezeichnet.
Ein Dreieck, dessen Winkel zwischen 90 ° und 180 ° liegt, wird als stumpfes Dreieck bezeichnet.
Ein Dreieck, dessen Winkel jeweils spitz ist, wird als spitzes Dreieck bezeichnet.
Die Summe aller Seiten eines Dreiecks wird als Umfang des Dreiecks bezeichnet.
Die Summe zweier Seiten eines Dreiecks ist größer als die dritte Seite.
In einem rechtwinkligen ABC mit ∠B = 90 ° haben wir AC ² = AB ² + BC ² . Dies nennt man Pythagoras-Theorem.

Viereck

Eine durch vier gerade Linien begrenzte Figur wird als Viereck bezeichnet. Die Summe aller Winkel eines Vierecks beträgt 360 °.

Rectangle- Ein Viereck wird als Rechteck bezeichnet, wenn seine gegenüberliegende Seite gleich ist und jeder Winkel 90 ° beträgt. In der angegebenen Abb. ABCD ist ein Rechteck.
Square- Ein Viereck wird als Quadrat bezeichnet, wenn alle Seiten gleich sind und jeder Winkel 90 ° beträgt. In der angegebenen Abb. ABCD ist ein Quadrat, in dem AB = BC = CD = DA ist.
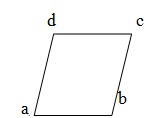
Parallelogram- Ein Viereck wird als Parallelogramm bezeichnet, wenn seine gegenüberliegenden Seiten parallel sind. In der angegebenen Abb. ABCD ist ein Parallelogramm, in dem AB = DC & AD = BC.
Rhombus- Ein Parallelogramm mit allen Seiten ist Rhombus. In der angegebenen Abb. ABCD ist eine Raute, in der AB = BC = CD = DA, AB || DC und AD || BC.

Wichtige Fakten

Ein Viereck ist ein Rechteck, wenn die gegenüberliegenden Seiten gleich sind und die Diagonalen gleich sind.
Ein Viereck ist ein Quadrat, wenn alle Seiten gleich und die Diagonale gleich sind.
Ein Viereck ist ein Parallelogramm, wenn die gegenüberliegenden Seiten gleich sind.
Ein Viereck ist ein Parallelogramm, aber kein Rechteck, wenn die gegenüberliegenden Seiten gleich sind, die Diagonalen jedoch nicht gleich sind.
Ein Viereck ist eine Raute, aber kein Quadrat, wenn alle Seiten gleich sind und die Diagonalen nicht gleich sind.

Ergebnisse auf Viereck

In einem Parallelogramm haben wir
1. Gegenüberliegende Seiten sind gleich.
2. Gegenüberliegende Winkel sind gleich.
3. Jede Diagonale halbiert das Parallelogramm.
4. Diagonalen eines Parallelogramms halbieren sich gegenseitig.
Diagonalen eines Rechtecks sind gleich.
Diagonalen einer Raute halbieren sich rechtwinklig.

Ergebnisse auf Kreis

Die Senkrechte von der Mitte zu einem Akkord halbiert den Akkord.
Es gibt nur einen Kreis, der durch drei nicht kollineare Punkte verläuft.
Der Winkel in einem Halbkreis ist ein rechter Winkel.
Gegenüberliegende Winkel eines zyklischen Vierecks ergänzen sich.
Der Winkel im gleichen Kreissegment ist gleich.
Die Tangente an einem beliebigen Punkt eines Kreises verläuft senkrecht zum Radius durch den Kontaktpunkt.
Zwei Tangenten an einen Kreis von einem Punkt außerhalb sind gleich.
Wenn PT eine Tangente an einen Kreis ist und PAB eine Sekante ist, dann ist PA x PB = PT ²

Gelöste Beispiele