Höhe & Entfernung - Gelöste Beispiele

F 1 - Von einem Punkt 375 Meter vom Fuß eines Turms entfernt wird die Spitze des Turms in einem Höhenwinkel von 45 ° beobachtet. Dann beträgt die Höhe (in Metern) des Turms?

A - 375

B - 450

C - 225

D - 250

Answer - A

Explanation

From the right angled triangle
Tan(45°)=  X/375
=> X = 375 m

Q 2 - Der Höhenwinkel eines Turms in einem Abstand von 90 m beträgt Feldbett ^-1 (4/5). Dann beträgt die Höhe des Turms

A - 45

B - 90

C - 112,5

D - 150

Answer - C

Explanation

Let cot^-1(4/5) = x 
=> cotx =  4/5   
=> tan(x) = 5/4   
From the right angled triangle
Tan(x) =  h/90 
=> h = 5/4*90 =112.5 m

F 3 - Auf ebenem Boden beträgt der Höhenwinkel der Turmspitze 30 °. Bei einer Annäherung von 20 Metern beträgt der Höhenwinkel 45 °. Dann beträgt die Höhe des Turms

A - 10

B - √3

C - 10√3

D - 20√3

Answer - C

Explanation

Let h be the height of tower
From figure.
20 =h (  cot30 - cot60)	
20 =h (√3-1/√3) 
=> 20√3 = h (3-1) 
=> h=10√3.

F 4 - Die Höhenwinkel der Spitzen zweier vertikaler Türme vom Mittelpunkt der Linien, die den Fuß der Türme verbinden, betragen 45 ° und 60 °. Das Verhältnis der Höhe der Türme beträgt

A - √3: 2

B - √3: 1

C - 2: √3

D - 2: 1

Answer - B

Explanation

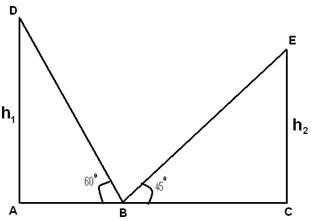
Tan(60)=h₁/AB
=> h1=√3AB
Tan(45)=h₁/BC
=> h2=BC
h1/ h2=√3/1
=> h1:h2=√3:1

F 5 - Die Höhe von zwei Türmen beträgt 90 Meter und 45 Meter. Die Linie, die ihre Spitzen verbindet, bildet einen Winkel von 450 zur Horizontalen, dann beträgt der Abstand zwischen den beiden Türmen

A - 22,5 m

B - 45 m

C - 60 m

D - 30 m

Answer - B

Explanation

Let the distance between the towers be X 
From the right angled triangle CFD 
Tan(45)=  (90-45)/X   
=> x=45 meters

Q 6 - Von einem Punkt P auf ebenem Boden beträgt der Höhenwinkel des oberen Turms 60 °. Wenn der Turm 180 m hoch ist, beträgt der Abstand von Punkt P vom Fuß des Turms

A - 60√3

B - 40√3

C - 30√3

D - 20√3

Answer - A

Explanation

From ∠APB = 60° and AB = 180 m.
AB/AP= tan 60° =√3
AP=AB/√3 =180/√3=60√3

F 7 - Die Spitze eines 25 Meter hohen Turms bildet mit der Unterseite eines Strommasts einen Höhenwinkel von 450 und mit der Spitze des Mastes einen Höhenwinkel von 30 Grad. Finden Sie die Höhe des Strommasts.

A - 25√3

B - 25 ((√3-1) / √3)

C - 25 / √3

D - 25 ((1 - √3) / √3)

Answer - B

Explanation

Let AB be the tower and CD be the electric pole. 
From the figure CA = DE
=> 25/(Tan(45))=(25-h)/(Tan(30))
=> 25  Tan(30) = 25-h
=> h=25-25Tan(30)
=25(1- Tan(30)) 
=25((√3-1)/√3)

F 8 - Ein 1,4 m großer Beobachter ist 10 √ 3 von einem Turm entfernt. Der Elevationswinkel von seinem Auge zur Turmspitze beträgt 60 °. Die Höhen des Turms sind

A - 12,4 m

B - 6,2 m

C - 11,4 √ 3 m

D - 11,4 m

Answer - D

Explanation

Let AB be the observer and CD be the tower.
Then, CE = AB = 1.4 m,
 BE = AC = 10v3 m.
DE/BE=Tan (30) =1/√3
DE=10√3/√3=10
CD=CE+DE=1.4+10=11.4 m

F 9 - Ein Mann beobachtet von der Spitze des Turms aus ein Boot, das vom Turm weg rast. Das Boot bildet mit dem Auge des Mannes in einer Entfernung von 75 Metern vom Turm einen Depressionswinkel von 60 °. Nach 10 Sekunden beträgt der Depressionswinkel 45 °. Was ist die ungefähre Geschwindigkeit des Bootes, vorausgesetzt es läuft in stillem Wasser?

A - 54 km / h

B - 64 km / h

C - 24 km / h

D - 19,8 km / h

Answer - D

Explanation

Let AB be the tower and C and D be the positions of the boat.
Distance travelled by boat = CD
From the figure 75tan(60)=(75+CD)tan(45)
=>75√3 = 75+CD
=>CD =55 m
Speed = distance/time=55/10
=5.5 m/sec=19.8 kmph

Q 10 - Der horizontale Abstand zwischen zwei Türmen beträgt 90 m. Die Winkelvertiefung der Oberseite der ersten, gesehen von der Oberseite der zweiten, die 180 m hoch ist, beträgt 450. Dann beträgt die Höhe der ersten

A - 90 √ 3 m

B - 45 m

C - 90 m

D - 150 m

Answer - C

Explanation