Argumentation - Uhr
Die Zeiger einer Uhr kann einen maximalen Winkel von 180 haben o zwischen ihnen. In diesem Fall stellen beide Hände eine gerade Linie dar.
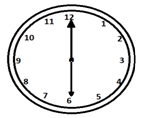
Die Zeiger einer Uhr bilden zweimal pro Stunde einen rechten Winkel, wenn sie 15 Minuten voneinander entfernt sind.
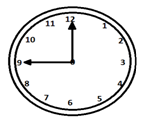
Die beiden Zeiger einer Uhr fallen einmal pro Stunde zusammen.
Eine Uhr ist für jeden Menschen sehr wichtig, um seine täglichen Aufgaben zu planen. Die Uhrentheorie bezieht sich auf den Alltag.
Eine Uhr ist ein Instrument, das die Zeit anzeigt, indem sie in Stunden, Minuten und Sekunden unterteilt wird.
Wählen
Es hat ein kreisförmiges Zifferblatt mit den Nummern 1 bis 12, das die Stunden anzeigt. Der Umfang eines Zifferblatts ist weiter in 60 gleiche Felder unterteilt, die als Minutenfelder bezeichnet werden.
1 Stunde = 60 Minuten
1 Minute = 60 Sekunden und
1 Stunde = 3600 Sekunden
Tricks
Zwischen n und (n + 1) Uhr fallen die beiden Zeiger einer Uhr bei $ \ left (\ frac {60n} {11} \ right) $ min nach n zusammen.
Zwischen n und (n + 1) Uhr bilden die beiden Zeiger einer Uhr einen rechten Winkel bei $ \ left (5n \ pm 15 \ right) \ times \ frac {12} {11} $ min nach n .
Zwischen n und (n + 1) Uhr befinden sich die Zeiger einer Uhr in einer geraden Linie (ohne zusammen zu sein) bei
$ \ left (5n - 30 \ right) \ times \ frac {12} {11} $ min nach n (wenn n> 6)
$ \ left (5n + 30 \ right) \ times \ frac {12} {11} $ min nach n (wenn n <6)
Zwischen n und (n + 1) Uhr sind die Zeiger einer Uhr $ x $ min voneinander entfernt bei $ \ left (5n \ pm x \ right) \ times \ frac {12} {11} $ min nach n. Das Zeichen '+' zeigt an, dass der Minutenzeiger voraus ist, und das Zeichen '-' zeigt an, dass der Stundenzeiger voraus ist.
Wenn der Minutenzeiger einer Uhr den Stundenzeiger in einem Intervall von $ x $ min der richtigen Zeit überholt, verliert oder gewinnt die Uhr um $ \ left (\ frac {720} {11} - x \ right) \ left (\ frac {60 \ times 24} {x} \ right) $ min.
1 - Zu welcher Zeit zwischen 7.15 und 8.15 Uhr stimmen die Zeiger einer Uhr überein?
Options - -
A - $ 39 \ frac {5} {11} $
B - $ 39 \ frac {4} {11} $
C - $ 38 \ frac {5} {11} $
D - $ 39 \ frac {4} {11} $
Answer - A.
Explanation - -
$ \ frac {60 \ times n} {11} = \ frac {60} {11} \ times \ frac {29} {4} = 39 \ frac {5} {11} $
Wobei $ n = 7,15 = 7 \ frac {15} {60} = \ frac {29} {4} $
2 - In welcher bestimmten Zeit, zwischen 9 und 8 Uhr, stehen beide Zeiger im rechten Winkel zueinander?
Options - -
A - $ 65 \ frac {4} {11} $ und $ 32 \ frac {7} {11} $ min nach 9
B - $ 65 \ frac {2} {11} $ und $ 32 \ frac {2} {11} $ min nach 9
C - $ 65 \ frac {3} {11} $ und $ 32 \ frac {3} {11} $ min nach 9
D - $ 65 \ frac {1} {11} $ und $ 32 \ frac {1} {11} $ min nach 9
Answer - A.
Explanation - -
$ \ left (5n \ pm 15 \ right) \ times \ frac {12} {11} = \ left (5 \ times9 \ pm 15 \ right) \ times \ frac {12} {11} $
$ = 65 \ frac {4} {11} $ und $ 32 \ frac {7} {11} $ min nach 9
3 - Wann bilden zwischen 12 und 1 Uhr beide Zeiger einer Uhr eine gerade Linie?
Options - -
A- $ \ frac {360} {11} $ min. nach 12
B- $ \ frac {355} {11} $ min. nach 12
C- $ \ frac {340} {11} $ min. nach 12
D- $ \ frac {345} {11} $ min. nach 12
Answer - D.
Explanation - -
$ \ left (5n-30 \ right) \ times \ frac {12} {11} $ min nach n
$ \ left (6-30 \ right) \ times \ frac {12} {11} $ min. nach 12
$ = \ frac {345} {11} $ min. nach 12 (da n = 12)
4- In wie viel Zeit sind Zeiger einer Uhr in den 30 Minuten. Platz auseinander, wenn sie am Montag zwischen 12 und 13 Uhr sind?
Options - -
A - $ \ frac {1080} {11} $ und $ \ frac {300} {11} $ min nach 12
B - $ \ frac {1080} {12} $ und $ \ frac {360} {11} $ min nach 12
C - $ \ frac {1080} {11} $ und $ \ frac {360} {11} $ min nach 12
D - $ \ frac {1080} {12} $ und $ \ frac {300} {12} $ min nach 12
Answer - C.
Explanation - -
$ \ left (5n \ pm x \ right) \ times \ frac {12} {11} $
$ = \ left (5 \ times12 \ pm 30 \ right) \ times \ frac {12} {11} $
$ = \ frac {90 \ times12} {11} $ und $ \ frac {30 \ times12} {11} $ min nach 12 = $ \ frac {1080} {11} $ und $ \ frac {360} {11} $ min nach 12
5- Der Minutenzeiger einer Uhr überholt den Stundenzeiger im Abstand von 61 Minuten. dann verliert oder gewinnt die Uhr um wie viel Zeit?
Options - -
A - $ 104 \ frac {4} {671} $ min.
B - $ 105 \ frac {1} {671} $ min.
C - $ 104 \ frac {3} {671} $ min.
D - $ 105 \ frac {4} {671} $ min.
Answer - B.
Explanation - -
$ \ left (\ frac {720} {11} -61 \ right) \ times \ left (\ frac {60 \ times24} {61} \ right) $
$ = 105 \ frac {1} {671} $ min.