Argumentation - Würfel und Quader

Heutzutage werden in fast jeder Wettbewerbsprüfung Fragen gestellt, die auf "Cubes and Cuboids" basieren. Diese Probleme treten bei verschiedenen Auswahlprüfungen sehr häufig auf.

Die unten beschriebenen Methoden sind einfach und doch elegant. Sie sollten sehr leicht zu verstehen sein und mit ein wenig Übung sollten Sie sie beherrschen. Ein Würfel ist ein dreidimensionaler Körper mit 6 Flächen, 12 Kanten und Ecken. Alle Kanten eines Würfels sind gleich und alle Flächen sind quadratisch. Das ist eine solide Figur mit 6 Gesichtern; Jedes Gesicht, das ein Quadrat ist, heißta cube. Wenn jede der sechs Flächen ein Rechteck ist, wird sie aufgerufencuboid. Ein Quader wird auch als a bezeichnetrectangular parallelepiped.

Es gibt folgende Arten von Fragen zu Würfeln und Quadern.

Tippe I

Es werden mehrere Ansichten eines vollständigen Würfels angezeigt, und Sie müssen herausfinden, welcher Teil des Würfels genau unter einem bestimmten Teil liegt.

Typ II

Ein geöffneter Würfel wird gegeben und Sie müssen vorhersagen, wie er aussehen wird, wenn er zu einem Würfel geschlossen wird.

Typ III

Ein Würfel konnte nicht auf oder einige seiner Flächen mit derselben Farbe oder verschiedenen Farben lackiert und dann in eine bestimmte Anzahl identischer Stücke geschnitten werden. Dann Frage der Form: "Wie viele kleine Würfel haben 2 lackierte Gesichter?" "Wie viele kleine Würfel haben nur ein Gesicht lackiert?" usw.

Es gibt zwei Arten von Problemen, die in der Prüfung auftreten. Zunächst erhalten Sie mehrere Ansichten von acomplete cubeund Sie müssen angeben, welcher Teil des Würfels genau unter einem bestimmten Teil liegt. In einem anderen Typ erhalten Sie eineopened-up cubeund Sie müssen vorhersagen, wie es aussehen wird, wenn es in einen Würfel geschlossen wird.

For Example - -

Unten sind mehrere Flächen eines Würfels dargestellt -

Welche Zahl würde 2 gegenüberliegen?

A - 1

B - 6

C - 5

D - 4

Der grundlegende Ansatz lautet wie folgt:

Tippe I

A fundamental rule: Opposite cannot be together;

Immer wenn wir einen Würfel sehen, von dem nur drei sichtbar sind, können wir niemals zwei gegenüberliegende Gesichter zusammen sehen. Mit all diesen Regeln können wir die oben diskutierte Art von Problem leicht lösen. In der obigen Frage, in der wir das gegenüberliegende Gesicht eines bestimmten Gesichts finden müssen, können wir diejenigen Gesichter eliminieren, die zusammen mit X in jeder Ansicht aufgetreten sind. Somit können wir jede andere Wahl eliminieren und der Rest wird unsere Antwort sein.

An dieser Stelle sollten Sie den vorherigen Absatz noch einmal durchgehen und sicherstellen, dass Sie das Konzept verstehen. Danach sollten Sie versuchen, das obige Beispiel zu lösen und zu prüfen, ob Sie das oben beschriebene Konzept anwenden können. Sie stellen jedoch fest, dass Sie das Konzept nicht vollständig verstanden haben, kein Problem. Lesen Sie diesen Abschnitt weiter. Sobald Sie den Abschnitt beendet haben, werden die Dinge klar. Mit der oben genannten Grundregel im Hinterkopf können Sie die oben genannte Art von Frage lösen.

Für die Frage ist die Regel an sich ausreichend. Danach können Sie es schneller lösen, indem Siethree secondary rules.

Solution for above example - -

Im gegebenen Beispiel müssen wir das Gesicht gegenüber von 2 finden. In der ersten Abbildung erscheint 2 zusammen mit 1 und 3. Dies bedeutet, dass weder 1 noch 3 gegenüber 2 sein können. Es bedeutet, dass wir das Gegenteil von 1 können haben entweder 4 oder 5 oder 6. In ähnlicher Weise können wir gegenüber 3 entweder 4 oder 5 oder 6 haben. Schauen Sie sich nun die zweite Abbildung an. Hier treten 3 und 1 zusammen mit 5 auf. Dies bedeutet, dass 5 weder 3 noch 1 entgegengesetzt ist. Dies bedeutet, dass entweder 4 oder 6 gegenüber 1 und das andere gegenüber 3 ist, sodass 5 gegenüber 2 sein muss. Daher ist 5 korrekt Antworten.

Einige schnellere Regeln

Jetzt müssen Sie den grundlegenden Trick zur Lösung solcher Fragen verstanden haben. Der Trick ist, dass Sie diejenigen Entscheidungen beseitigen sollten, die nicht möglich sind. Dazu helfen Sie einer Grundregel, die besagt, dass wenn zwei Flächen einander gegenüberliegen, ihr gleichzeitiges Auftreten in einer Ansicht des Würfels nicht möglich ist. In den heutigen zeitintensiven Wettbewerben reicht jedoch nur das Konzept nicht aus. Sie müssen in der Lage sein, eine Frage schnell zu lösen. Es gibt einige sekundäre Regeln zum Lösen von Fragen.

Rule I- Nennen wir diese Figur X, deren Gegenteil Sie finden müssen. Angenommen, in einer Ansicht des Würfels erscheint X mit Y und Z. Zusammen mit einer dritten Zahl (sagen wir A) ist X gegenüber A.

Wie zum Beispiel müssen Sie das Gesicht gegenüber 2 finden. (Dies ist unser X). Jetzt erscheint 2 in einer Figur zusammen mit 1 und 3. (Y und Z). Auch 1 und 3 erscheinen zusammen in einer weiteren Figur zusammen mit 5. (Das ist A). Daher muss 2 gegenüber 5 sein.

Rule II- Wir müssen das gegenüberliegende Gesicht von 'X' finden. Angenommen, in einer Ansicht des Würfels wird X mit Y und Z angezeigt. Angenommen, Y und Z werden in keiner weiteren Ansicht zusammen angezeigt, sondern in zwei oder mehr verschiedenen Ansichten getrennt. Dann ist die gemeinsame Figur zwischen den beiden weiteren Ansichten, in denen Y und Z getrennt erscheinen, die Figur gegenüber X.

Rule III- Nennen wir die Figur X, deren Gegenteil Sie finden müssen. Angenommen, X erscheint in zwei Ansichten und in diesen beiden Ansichten werden vier verschiedene Figuren mit X gesehen. Dann muss die einzige Figur, die in diesen beiden Ansichten nicht mit X gesehen wird, X gegenüberliegen.

Summary- Sie müssen die Grundregel im Hinterkopf behalten und dann drei sekundäre Regeln anwenden, um schnelle Antworten zu erhalten. Der gesamte Ansatz kann anhand des folgenden Diagramms zusammengefasst werden.

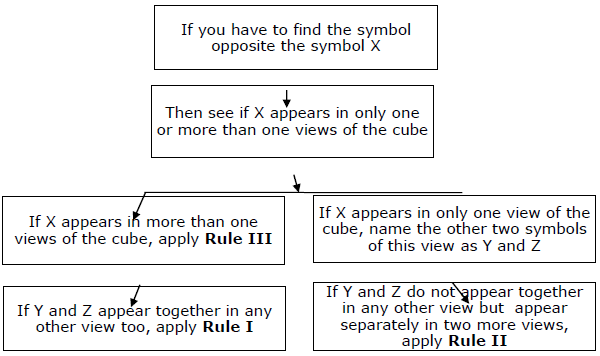
Typ II

Bei diesem Typ verwenden wir die Grundregel. Diese Regel hilft uns, jene Kombinationen zu eliminieren, bei denen gegenüberliegende Flächen in einer einzigen Ansicht angezeigt werden. Es wird also zur Eliminierung einer Wahl führen, vorausgesetzt, wir wissen, wie wir bestimmen können, welches Gesicht einander entgegengesetzt sein wird, indem wir uns das „opened-up cube”. Zu diesem Zweck gibt es eine sehr einfache Regel, anhand derer Sie anhand deropened-up cube, welche Gesichter sich gegenüberliegen, wenn man sie nur ansieht.

Die Regel ist unten angegeben;

Third is opposite rule - -

Wenn Sie das gegenüberliegende Gesicht eines Gesichts (z. B. X) in Abbildung I, II, III herausfinden möchten; Ein geöffneter Würfel wird gegeben. Wir müssen herausfinden, welche Flächen sich gegenüberliegen, wenn der Würfel geschlossen ist.

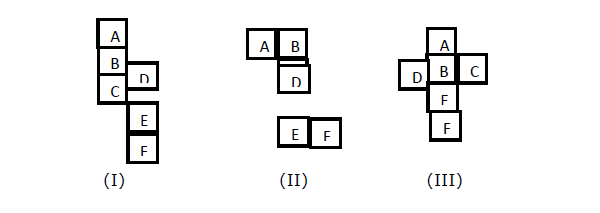
Explanation - -

In Abbildung (I) ist die dritte Zahl zu A C. Also ist A entgegengesetzt zu C. Also sind D und F entgegengesetzt. B und E sind entgegengesetzt.

In Abbildung (II) steht B an dritter Stelle zu D, sodass B gegenüber D steht. In ähnlicher Weise ist C gegenüber E und A gegenüber F.

In Fig. (III) ist A gegenüber E, B gegenüber F. Daher ist C gegenüber D.

Steps to solve problem

Wir können jetzt Fragen dieser Art lösen. Wir wissen, wie wir das gegenüberliegende Gesicht finden, indem wir uns ein ansehenOpened-up cube. Wir wissen auch, dass in jeder Ansicht des Würfels gegenüberliegende Flächen nicht zusammen sein können. Wenn wir also zwei Regeln kombinieren, können wir Probleme leicht lösen.

Zusammenfassung

Damit ist die Diskussion zur Lösung von Fragen des Typs II abgeschlossen. Sie müssen die dritte Regel verwenden, um zu bestimmen, welche Gesichter einander gegenüberliegen. Das folgende Diagramm enthält die vollständigen Informationen zu diesem Ansatz.

Typ III

Counting of Cubes (when a varnished solid cube is cut);

Im vorherigen Abschnitt haben wir das Problem des Findens der gegenüberliegenden Seite eines Würfels erörtert. Es gibt eine andere Art von Frage in Bezug auf Würfel, bei der ein größerer Würfel mit verschiedenen Farben, die auf verschiedenen Seiten lackiert sind, in mehrere kleinere Würfel aufgeteilt wird und Sie die Anzahl der Würfel ermitteln müssen, bei denen nur eine Seite oder zwei Seiten lackiert sind.

Format of this problem - -

Example - -

Ein Würfel ist mit drei Farben grün, blau und rot an den Seiten lackiert, wobei jede Farbe auf zwei gegenüberliegenden Seiten des Würfels lackiert ist. Jetzt wird der Würfel in 64 gleich große Würfel aufgeteilt. Beantworten Sie anhand dieser Informationen die folgenden Fragen:

1. Wie viele Würfel haben zwei Seiten lackiert und die restlichen Seiten unlackiert?

A - 18

B - 20

C - 22

D - 24

2. Wie viele Würfel haben nur eine Seite lackiert (entweder nur mit grüner oder blauer Farbe)?

A - 4

B - 24

C - 16

D - 12

3. Wie viele Würfel haben keine lackierten Seiten?

A - 0

B - 8

C - 12

D - 64