Argumentation - Logischer Abzug
Der logische Abzug ist ein wichtiges Kapitel, da viele einfache und markenbezogene Fragen aus diesem Kapitel in verschiedenen Auswahlprüfungen enthalten sind. In diesem Kapitel werden zwei Methoden zur Lösung solcher Probleme erörtert:
- Syllogismus-Methode
- Venn-Diagrammmethode
Grundlagen
Wenn es zwei Aussagen gibt, ist Syllogismus der beste Weg, um das Problem zu lösen. Wenn die Anzahl der Aussagen jedoch mehr als zwei beträgt, wählen Sie die Venn-Diagrammmethode. Manchmal werden Aussagen und Schlussfolgerungen aus allgemein anerkannten Tatsachen abgeleitet, aber sie können auch nicht logisch sein. Zum Beispiel -
a) Einige Stühle sind Türen.
b) Alle Männer sind Frauen
c) Keine Milch ist weiß
Um zu dem Schluss zu kommen, ist abstraktes Denken erforderlich. Man muss den logischen Sinn des Satzes verstehen und dann die Schlussfolgerungen entsprechend beantworten. Jede Aussage muss als wahr angesehen werden, dann müssen wir überprüfen, ob die Schlussfolgerungen logisch den Aussagen folgen.
Qualifikanten
Dies sind einige der elementaren Wörter, die verwendet werden, um zu beschreiben, wie sehr eine Sache der anderen ähnlich oder verschieden ist. Beispiele für einige der Qualifikanten sind "Alle", "Einige", "Einige-nicht" usw.
Venn-Diagrammkonzept
Andererseits ist das Venn-Diagramm ein Prozess, bei dem wir einen Satz oder eine Aussage in Form von geometrischen Figuren darstellen können. Alle angegebenen Aussagen sind in möglichen Venn-Diagrammen dargestellt. Dann werden alle Schlussfolgerungen mit diesen Diagrammen überprüft. Jede Schlussfolgerung, die alle Venn-Diagramme erfüllt, wird als gültige Schlussfolgerung betrachtet.
| Aussagen | Entsprechende Venn-Diagramme |
|---|---|
| Alle A sind B. |
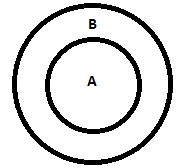
|
| Einige A sind B (ODER) Einige A sind nicht B. |
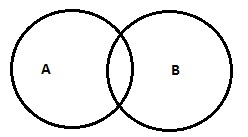
|
| Nein A ist B. |
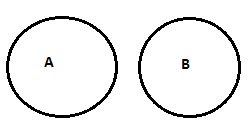
|
Nehmen wir ein einfaches Beispiel, um es besser zu verstehen.
Sample − 1
Statements - -
Alle Ingenieure sind Dummköpfe. Alle Dummköpfe sind Ärzte. Alle Ärzte sind arm.
Conclusions - -
I. Einige Arme sind Dummköpfe.
II. Einige Arme sind Ingenieure.
Options - -
A - Nur ich ist gültig
B - Nur II ist gültig
C - Beide Aussagen sind gültig
D - Keine der Aussagen ist gültig
Answer - Option C.
Explanation - -
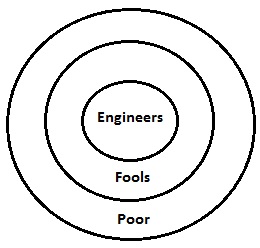
Das Venn-Diagramm für die angegebenen Aussagen ist oben dargestellt. Es zeigt alle Aussagen schematisch an einer Stelle. Wenn wir jetzt nacheinander über die Schlussfolgerungen diskutieren, wird alles klar sein.
Hier sind Narren eine Untergruppe der Armen. Es ist also eine offensichtliche Tatsache, dass einige Arme Dummköpfe sein werden. Daher ist Schlussfolgerung I gültig. In ähnlicher Weise gilt Schlussfolgerung II, da Ingenieure auch eine Untergruppe von Armen sind. Daher sind beide Aussagen gültig.
Sample − 2
Statements - -
Einige Tastaturen sind Maus. Einige Mäuse sind Radios.
Conclusions - -
I. Einige Tastaturen sind Radios.
II. Einige Radios sind Tastaturen
III. Alle Radios sind Maus.
IV. Alle Mäuse sind Tastaturen.
Options - -
A - Nur Schlussfolgerung I ist gültig
B - Nur Schlussfolgerung II ist gültig
C - Entweder I oder II ist gültig
D - Keine der Schlussfolgerungen ist gültig
E - Sowohl I als auch II sind gültig
Answer - Option D.
Explanation - Da beide Aussagen spezifisch sind, ist keine endgültige Schlussfolgerung gültig.
Sample − 3
Statements - -
Alle Schüler sind nüchtern. Alle Schüler sind ungezogen.
Conclusions - -
I. Alle Unartigen sind entweder nüchtern oder umgekehrt.
II. Einige nüchterne Personen sind ungezogen.
III. Im Allgemeinen sind ungezogen nüchtern.
IV. Verbrechen und Schuld gehören zusammen.
Options - -
A - Nur Schlussfolgerung I ist gültig
B - Nur Schlussfolgerung II ist gültig
C - Entweder I oder II ist gültig
D - Keines der I oder II ist gültig
E - Sowohl I als auch II sind gültig
Answer - Option B.
Explanation- Da der Zwischenbegriff „Studenten“ in den Aussagen zweimal verteilt ist, kann die Schlussfolgerung nicht weit gefasst werden. Es ist also gültig, dass "einige nüchterne Personen ungezogen sind". Somit gilt II.