Argumentation - Syllogismus
Die Bedeutung des Syllogismus, wie er von den Griechen gegeben wird, ist Deduction. Es ist eine Art logische Argumentation.
Definition einiger wichtiger Begriffe
Im Folgenden werden einige Begriffe aufgeführt, die eine wichtige Rolle bei der Lösung von Syllogismusproblemen spielen.
Proposition- Satz ist ein Satz, der Aussagen macht. Der Satz besteht aus 3 Teilen: a) Subjekt, b) Prädikat und c) Beziehung zwischen Subjekt und Prädikat. Einige Vorschläge sind unten angegeben.
- Alle Küsten sind Strände.
- Keine Schüler sind ehrlich.
- Einige Dokumente sind geheim.
Subject and Predicate- Thema ist der Teil, über den etwas gesagt wird. Andererseits ist Prädikat der Teil, der sich auf das Subjekt bezieht. Zum Beispiel - von den oben genannten Aussagen Küsten, Studenten, Dokumente sind Themen, während Strände, ehrlich und geheim Prädikate sind.
Arten von kategorialen Aussagen
Universal Proposition- Universeller Satz ist der, der das Thema entweder vollständig einschließt oder ganz ausschließt. Zum Beispiel: Keine Schüler sind schlau. Der universelle Satz wird weiter unterteilt in:
Universal positive proposition - Wenn das Formular ist all X are Ydann heißt es positiver Satz. Es wird im Allgemeinen mit einem Buchstaben bezeichnetA.
Universal negative proposition - Wenn das Formular ist no X are Tdann heißt es negativer Satz. Es wird mit bezeichnetE.
Particular proposition- Es ist der Satz, der das Thema teilweise zeigt oder teilweise, aber nicht vollständig ausschließt. Zum Beispiel sind einige Katzen Baumwolle. Es ist auch in folgende Typen unterteilt:
Particular positive proposition - Formen wie some X are Uwerden als besonders positiver Satz bezeichnet. Sie sind codiert alsI.
Particular negative proposition - Formen wie Some T are not P zum Beispiel, some cats are not coils wird als besonderer negativer Satz bezeichnet und als kodiert O.
Mediate inference- Hier wird aus zwei Aussagen geschlossen. Beispiel - "Alle Lippen sind Spulen" und "Alle Kugeln sind Fledermäuse". Die Schlussfolgerung lautet also „Alle Lippen sind Spulen“.
Immediate inference- Hier wird nur aus einem Satz geschlossen. Wenn zum Beispiel die Aussage lautet: "Alle Lehrer sind Gott", lautet die Schlussfolgerung "Einige Lehrer sind Gott".
Zwei wichtige Methoden der unmittelbaren Folgerung
Diese Methoden umfassen Umwandlung, Kontraposition usw.
Implications- Angenommen, „alle Katzen sind Strände“, dann zeigt dies, dass die Schlussfolgerung „einige Katzen sind Strände“ wahr ist. Wenn also ein gegebener Satz der Kategorie A angehört, zeigt dies auch, dass die Schlussfolgerung vom Typ I wahr sein muss.
Conversion - Es besteht aus 2 Schritten.
Step 1 - Das Thema wird in ein Prädikat umgewandelt und umgekehrt.
Step 2 - Der gegebene Vorschlag wird entsprechend geändert.
For Example −
Statements- Alle Katzen sind Gestelle. Alle Taschen sind Gestelle. Einige Geldbörsen sind Taschen.
Conclusions - -
1. Einige Katzen sind Taschen.
2. Einige Gestelle sind Katzen.
3. Einige Gestelle sind Geldbörsen.
A - Nur 1
B - Nur 2 und 3
C - Nur 1 und 2
D - Nur 1 und 3
Solution −
Antwort - Option B.
Die bildliche Darstellung von Sätzen wird von Euler formuliert. Es gibt vier Möglichkeiten, wie die Beziehung nach vier Sätzen hergestellt werden kann.
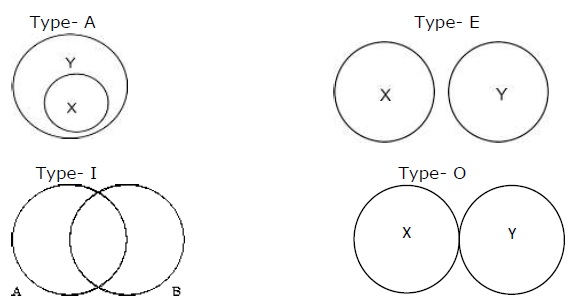
Typ - A steht für "Alle X sind Y", Typ - E steht für "Kein X ist Y", Typ - I steht für "Einige A sind B" und Typ - O steht für "Einige X sind nicht Y".
For Example −
Statements −Einige Kameras sind Laptops.
Einige Laptops sind Telefone.
Einige Telefone sind Tablets.
Conclusions −
I - Zumindest einige Tablets sind Kameras
II - Es besteht die Möglichkeit, dass alle Tablets Laptops sind
III - Keines der Tablets ist ein Laptop
Solution −
Kreisdiagramm -
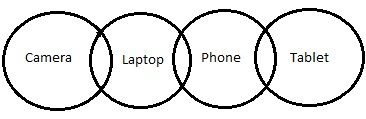
Gemäß obigem Diagramm
Schlussfolgerung III folgt. In der Erklärung wurde jedoch das Wort "Möglichkeit" erwähnt. Lassen Sie uns also nach den Möglichkeiten suchen.
Neues Diagramm wird sein -
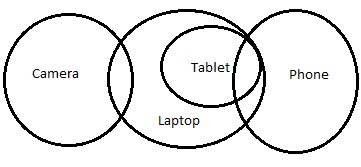
In diesem Fall folgt jedoch nicht die Schlussfolgerung III. Es folgt entweder Schlussfolgerung II oder Schlussfolgerung III.