Argumentation - Codierte Binärzahlen
Die Zahl mit der Basis 2 wird als Binärzahl bezeichnet. Die Binärzahl wird durch die Komplemente von 0 und 1 gebildet. Die codierte Binärzahl besteht also aus zwei Prozessen. Eine ist die Umwandlung von Binär in Dezimal und eine andere ist Dezimal in Binär.
Dezimal Zahlen
Um zu wissen was binary numberist, zuerst müssen wir über Dezimalzahlen wissen. Die Dezimalzahl besteht also aus zehn Ziffern (dh 0,1,2,3,4,5,6,7,8,9). Mit diesen Zahlen kann jedes Dezimalsystem dargestellt werden. Zum Beispiel ist eine Folge von Ziffern 2, 4, 6 und 8. Wir machen das auf folgende Weise:
2468 = 2 × 10 3 + 4 × 10 2 + 6 × 10 1 + 8 × 10 0
= 2468
Note- In diesem Fall erhalten wir den Wert von Zahlen, indem wir verschiedene Ziffern der Sequenz mit Potenzen von 10 multiplizieren und addieren. Hier wird diese 10 Basis oder Radix genannt. Daher ist unsere Basis unter einem Dezimalsystem 10.
Binärzahlen
Wir verwenden zehn Ziffern, um a darzustellen decimal number;; so verwenden wir nur zwei Ziffern, um die Binärzahl darzustellen. Mit diesen beiden Ziffern, dh 0 und 1, kann jede Zahl dargestellt werden.
Beispiel für eine Binärzahl ist - 1101. Hier sind 4 Ziffern in der Ziffernfolge vorhanden - 1, 1, 0, 1. Wir erhalten den Wert auf folgende Weise.
1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0
= 8 + 4 + 0 + 1 = 13
Somit repräsentiert die Binärzahl dreizehn im Dezimalsystem. Der Wert kann bestimmt werden durchmultiplying different digits der Reihenfolge durch Potenzen von 2 und Addition.
Conventional method - Im obigen Beispiel sehen wir, dass wir die folgende Regel verwenden, um den Wert einer beliebigen Binärzahl zu erhalten:
Die erste Ziffer von rechts wird mit 2 0 = 1 multipliziert
Die zweite Ziffer von rechts wird mit 2 1 = 2 multipliziert
Die dritte Ziffer von rechts wird mit 2 2 = 4 multipliziert
In ähnlicher Weise wird die n- te Ziffer von rechts mit 2 n - 1 multipliziert
Schließlich werden alle diese hinzugefügt.
For Example - Konvertieren Sie die folgenden Binärzahlen in Dezimalzahlen.
A - 1010
B - 1111
C - 100
D - 10000
Solution - -
A - 1010 = 1 × 2 3 + 0 × 2 2 + 1 × 2 1 + 0 × 2 0
B - 1111 = 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0
C - 100 = 1 × 2 2 + 0 × 2 1 + 0 × 2 0
D - 10000 = 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 0 × 2 0
Schnellere Methode
Step I- Schreiben Sie ausgehend von der rechten Ziffer der angegebenen Nummer 1, 2, 4, 8, 16, 32 ……. und so weiter unter jeder Ziffer, wenn Sie nach links gehen.
Step II- Ignorieren Sie die Zahlen unter 0s. Addiere alle Zahlen unter 1s.
Lösen wir das Beispiel 1 mit dieser Methode.
A - 1010
Wir werden 1,2,4,8 verwenden, da hier 4 Ziffern vorhanden sind.
Wir bekommen,
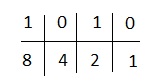
4 und 1 fallen unter die Nullen. Wir ignorieren sie und fügen die restlichen hinzu. Wir erhalten 8 + 2 = 10
So können wir andere Zahlen lösen.
Die Dezimalzahl kann nach der Methode von in eine Binärzahl umgewandelt werden successive divisions. Bei jeder Teilung wird die Dividende durch 2 geteilt. Die Erinnerung wird notiert und der Quotient wird zur nächsten Dividende, die wiederum durch 2 geteilt wird. Der Vorgang wird wiederholt, bis keine weitere Teilung mehr möglich ist.
Zum Beispiel - konvertiere 17 in eine Binärzahl -
Teilen Sie 17 durch 2, bis keine Teilung mehr möglich ist.
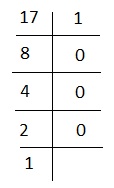
Die binäre Form von 17 ist also 10001.
Direction (Q. 1-4) − Study the following question and give the answer.
In einem bestimmten Code ist das Symbol für 0 + und für 1 #. Keine Zahl oder kein Symbol ist größer als 1. Der Wert des Symbols für 1 verdoppelt sich jedes Mal, wenn es um eine Stelle nach links verschoben wird.
'0' wird als + dargestellt
'1' wird als # dargestellt
'2' wird als # + dargestellt
'3' wird als ## dargestellt
'4' wird als # ++ dargestellt und so weiter
1 - Welche der folgenden Aussagen steht für 11?
Options - -
A - # + ##
B - + ## +
C - ## ++
D - # + # ++
E - keine von diesen
Answer - Option A.
Explanation - Um das Äquivalent von 11 zu erhalten, verwenden wir die Methode der sukzessiven Division durch 2.

Die binäre Form ist also 10111. Wenn Sie 1 und 0 durch # und + ersetzen, erhalten Sie # + ##.
2 - Welche der folgenden Aussagen steht für 8?
Options - -
A - ## ++
B - + ## +
C - ## ++
D - ++ ##
E - keine von diesen
Answer - Option E.
Explanation - für 8 haben wir-
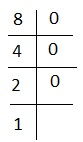
dh 1000 oder # +++. Die richtige Wahl ist 5.
3 - Welche der folgenden Optionen wird durch ## + # dargestellt?
Options - -
A - 8
B - 11
C - 13
D - 12
E - keine von diesen
Answer - Option E.
Explanation- ## + # = 1101 = 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 = 15
4 - Welche der folgenden Zahlen wird durch # +++ # dargestellt?
Options - -
A - 22
B - 31
C - 14
D - 17
E - keine von diesen
Answer - Option D.
Explanation - # + + + # = 10001
= 1 × 2 4 + 0 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0
= 16 + 1 = 17
Binäre Systeme haben Basis 2, ein Dezimalsystem hat Basis 10 und Tertiärsystem hat Basis 3, während Oktalsystem Basis 8 hat. Im Tertiärsystem haben wir drei Ziffern, um Zahlen darzustellen. Dies sind 0, 1 und 2. In diesem Fall werden Zahlen durch Multiplikation mit geeigneten Potenzen von 3 in Dezimalzahlen umgewandelt.
For Example - -
(12012) 3 = 1 × 3 4 + 2 × 3 3 + 0 × 3 2 + 1 × 3 1 + 2 × 3 0 = (104) 3