Kosmologi - Panduan Cepat
Cosmologyadalah studi tentang alam semesta. Menilik ke masa lalu, ada beberapa aliran pemikiran tentang asal mula alam semesta. Banyak sarjana percaya padaSteady State Theory. Menurut teori ini, alam semesta selalu sama, tidak memiliki awal.
Padahal ada sekelompok orang yang beriman kepada Big Bang Theory. Teori ini memprediksi awal mula alam semesta. Ada bukti radiasi panas yang tertinggal dari Big Bang, yang sekali lagi mendukung model tersebut. Teori Big Bang memprediksi kelimpahan elemen cahaya di alam semesta. Jadi, mengikuti model Big Bang yang terkenal, kita dapat menyatakan bahwa alam semesta memiliki permulaan. Kita hidup di alam semesta yang mengembang.
The Hubble Redshift
Pada awal 1900-an, teleskop canggih, Mt Wilson, Teleskop 100 inci, adalah teleskop terbesar saat itu. Hubble adalah salah satu ilmuwan terkemuka, yang bekerja dengan teleskop itu. Ia menemukan ada galaksi di luar Bima Sakti.Extragalactic Astronomybaru berusia 100 tahun. Mt Wilson adalah teleskop terbesar sampai dibangun Observatorium Palmer yang memiliki teleskop 200 inci.
Hubblebukan satu-satunya orang yang mengamati galaksi di luar Bima Sakti, Humason membantunya. Mereka mulai mengukur spektrum galaksi terdekat. Mereka kemudian mengamati spektrum galaksi berada pada rentang panjang gelombang yang terlihat dengan emisi terus menerus. Ada garis emisi dan serapan di atas kontinum. Dari garis-garis ini, kita dapat memperkirakan apakah galaksi bergerak menjauh dari kita atau ke arah kita.
Saat kita mendapatkan spektrum, kita asumsikan garis terkuat berasal H-α. Dari literatur, garis terkuat harus muncul di6563 Å, tetapi jika garis tersebut muncul di suatu tempat di sekitar 7000Å, kami dapat dengan mudah mengatakan itu bergeser merah.
Dari Special Theory of Relativity,
$$1 + z = \sqrt{\frac{1+\frac{v}{c}}{1-\frac{v}{c}}}$$
dimana, Z adalah pergeseran merah, bilangan tak berdimensi dan v adalah kecepatan resesi.
$$\frac{\lambda_{obs}}{\lambda_{rest}} = 1 + z$$
Hubble dan Humason mencatat 22 Galaxiesdi kertas mereka. Hampir semua galaksi ini menunjukkan pergeseran merah. Mereka menggambarkan kecepatan (km / s) vs jarak (Mpc). Mereka mengamati tren linier dan Hubble mengajukan hukumnya yang terkenal sebagai berikut.
$$v_r = H_o d$$
Ini adalah Hubble Redshift Distance Relationship. Subskriprmenunjukkan ekspansi ke arah radial. Sementara,$v_r$ adalah kecepatan surut, $H_o$ adalah parameter Hubble, dadalah jarak galaksi dari kita. Mereka menyimpulkan bahwa galaksi yang jauh surut lebih cepat dari kita, jika laju perluasan alam semesta seragam.
Pengembangan
Semuanya menjauh dari kita. Galaksi tidak diam, selalu ada beberapa ekspansi harmonik. Satuan parameter Hubble adalah km sec −1 Mpc −1 . Jika seseorang keluar dalam jarak - 1 Mpc, galaksi akan bergerak dengan kecepatan 200 km / detik. Parameter Hubble memberi kita laju ekspansi. Sesuai Hubble dan Humason, nilai$H_o$ adalah 200 km / detik / Mpc.
Data menunjukkan semua galaksi menjauh dari kita. Jadi, jelaslah bahwa kita berada di pusat alam semesta. Tapi Hubble tidak membuat kesalahan ini, menurut dia, di galaksi manapun kita tinggal, kita akan menemukan semua galaksi lain menjauh dari kita. Dengan demikian, kesimpulannya adalah bahwa ruang antar galaksi mengembang dan tidak ada pusat alam semesta.
Ekspansi terjadi dimana-mana. Namun, ada beberapa kekuatan yang menentang ekspansi. Ikatan kimiawi, gaya gravitasi, dan gaya menarik lainnya mengikat benda-benda. Sebelumnya semua objek saling berdekatan. Mengingat Big Bang sebagai gaya impulsif, benda-benda ini diatur untuk menjauh satu sama lain.
Skala Waktu
Pada skala lokal, Kinematika diatur oleh Gravitasi. Dalam hukum Hubble yang asli, ada beberapa galaksi yang menunjukkan pergeseran biru. Ini dapat dikreditkan ke potensi gravitasi gabungan dari galaksi. Gravitasi telah memisahkan hal-hal dari hukum Hubble. Galaksi Andromeda mendekati kita. Gravitasi mencoba memperlambat segalanya. Awalnya ekspansi melambat, sekarang semakin cepat.
Ada Cosmic Jerkkarena ini. Beberapa perkiraan untuk parameter Hubble telah dibuat. Ini telah berkembang selama 90 tahun dari 500 km / detik / Mpc menjadi 69 km / detik / Mpc. Perbedaan nilai itu karena jarak yang diremehkan. ItuCepheid Stars digunakan sebagai kalibrator jarak, namun terdapat berbagai jenis bintang Cepheid dan fakta ini tidak dipertimbangkan untuk estimasi parameter Hubble.
Waktu Hubble
Konstanta Hubble memberi kita perkiraan realistis usia alam semesta. Itu$H_o$akan memberikan usia alam semesta asalkan galaksi-galaksi itu bergerak dengan kecepatan yang sama. Kebalikan dari$H_o$ memberi kita waktu Hubble.
$$t_H = \frac{1}{H_o}$$
Mengganti nilai sekarang dari $H_o, t_H$ = 14miliar tahun. Laju ekspansi konstan sepanjang permulaan alam semesta. Bahkan jika ini tidak benar,$H_o$memberikan batasan yang berguna tentang usia alam semesta. Dengan asumsi laju ekspansi konstan, ketika kita memplot grafik antara jarak dan waktu, kemiringan grafik ditentukan oleh kecepatan.
Dalam hal ini, waktu Hubble sama dengan waktu sebenarnya. Namun, jika alam semesta mengembang lebih cepat di masa lalu dan lebih lambat di masa sekarang, waktu Hubble memberikan batas atas usia alam semesta. Jika alam semesta mengembang perlahan sebelumnya, dan semakin cepat sekarang, maka waktu Hubble akan memberikan batas bawah usia alam semesta.
$t_H = t_{age}$ - jika laju muai konstan.
$t_H > t_{age}$ - jika alam semesta telah berkembang lebih cepat di masa lalu dan lebih lambat di masa sekarang.
$t_H < t_{age}$ - jika alam semesta mengembang lebih lambat di masa lalu dan lebih cepat di masa sekarang.
Bayangkan sekelompok 10 galaksi yang berada pada 200 Mpc dari kelompok galaksi lain. Galaksi-galaksi dalam gugus tidak pernah menyimpulkan bahwa alam semesta mengembang karena kinematika dalam gugus lokal diatur oleh gravitasi.
Poin untuk Diingat
Kosmologi adalah studi tentang masa lalu, sekarang, dan masa depan alam semesta kita.
Alam semesta kita berusia ∼14 miliar tahun.
Alam semesta terus berkembang.
Parameter Hubble adalah ukuran umur alam semesta.
Nilai saat ini dari Ho adalah 69 kms / detik / Mpc.
Untuk waktu yang sangat lama, tidak ada yang menganggap galaksi ada di luar Bima Sakti kita. Pada tahun 1924, Edwin Hubble terdeteksiCepheid’sdi Nebula Andromeda dan memperkirakan jarak mereka. Dia menyimpulkan bahwa "Nebula Spiral" ini sebenarnya adalah galaksi lain dan bukan bagian dari Bima Sakti kita. Oleh karena itu, ia menetapkan bahwa M31 (Galaksi Andromeda) adalah Alam Semesta Pulau. Ini adalah kelahiranExtragalactic Astronomy.
Pertunjukan Cepheid a periodic dip in their brightness. Pengamatan menunjukkan bahwa periode antara penurunan berturut-turut yang disebut periode denyut berhubungan dengan luminositas. Jadi, mereka bisa digunakan sebagai indikator jarak. Bintang deret utama seperti Matahari berada dalam kesetimbangan hidrostatik dan mereka membakar hidrogen di intinya. Setelah hidrogen terbakar sepenuhnya, bintang-bintang bergerak menuju fase Raksasa Merah dan mencoba untuk mendapatkan kembali kesetimbangannya.
Bintang Cepheid adalah bintang Urutan Utama pos yang sedang transit dari bintang Urutan Utama ke Red Giants.
Klasifikasi Cepheid
Ada 3 kelas besar dari bintang variabel yang berdenyut ini -
Type-I Cepheids (atau Cepheid Klasik) - periode 30-100 hari.
Type-II Cepheids (atau W Virginis Stars) - periode 1-50 hari.
RR Lyrae Stars - periode 0.1-1 hari.
Saat itu, Hubble tidak mengetahui klasifikasi bintang variabel ini. Itulah mengapa ada perkiraan berlebihan dari konstanta Hubble, karena itu dia memperkirakan usia alam semesta kita lebih rendah. Jadi, kecepatan resesi juga terlalu tinggi. Di Cepheid, gangguan menyebar secara radial ke luar dari pusat bintang sampai kesetimbangan baru tercapai.
Hubungan antara Kecerahan dan Periode Pulsasi
Sekarang, mari kita coba memahami dasar fisik dari fakta bahwa periode pulsasi yang lebih tinggi menyiratkan lebih banyak kecerahan. Pertimbangkan bintang luminositas L dan massa M.
Kami tahu bahwa -
$$L \propto M^\alpha$$
di mana α = 3 hingga 4 untuk bintang bermassa rendah.
Dari Stefan Boltzmann Law, kami tahu bahwa -
$$L \propto R^2 T^4$$
Jika R adalah radius dan $c_s$ adalah kecepatan suara, lalu periode denyut P dapat ditulis sebagai -
$$P = R/c_s$$
Tetapi kecepatan suara melalui media apa pun dapat dinyatakan dalam suhu sebagai -
$$c_s = \sqrt{\frac{\gamma P}{\rho}}$$
Sini, γ adalah 1 untuk kasus isotermal.
Untuk gas ideal, P = nkT, di mana k adalah Boltzmann Constant. Jadi, kita bisa menulis -
$$P = \frac{\rho kT}{m}$$
dimana $\rho$ adalah kepadatan dan m adalah massa proton.
Oleh karena itu, periode diberikan oleh -
$$P \cong \frac{Rm^{\frac{1}{2}}}{(kT)^{{\frac{1}{2}}}}$$
Virial Theorem menyatakan bahwa untuk distribusi bola benda bermassa sama yang stabil, gravitasi sendiri, dan bulat (seperti bintang, galaksi), energi kinetik total k objek sama dengan minus setengah dari total energi potensial gravitasi u, yaitu,
$$u = -2k$$
Mari kita asumsikan bahwa teorema virial berlaku untuk bintang variabel ini. Jika kita menganggap proton tepat di permukaan bintang, maka dari teorema virial kita dapat mengatakan -
$$\frac{GMm}{R} = mv^2$$
Dari distribusi Maxwell,
$$v = \sqrt{\frac{3kT}{2}}$$
Oleh karena itu, titik -
$$P \sim \frac{RR^{\frac{1}{2}}}{(GM)^{\frac{1}{2}}}$$
yang menyiratkan
$$P \propto \frac{R^{\frac{3}{2}}}{M^{\frac{1}{2}}}$$
Kami tahu bahwa - $M \propto L^{1/\alpha}$
Juga $R \propto L^{1/2}$
Maka untuk β > 0, akhirnya kami mendapatkan - $P \propto L^\beta$
Poin untuk Diingat
Bintang Cepheid adalah bintang Urutan Utama pos yang transit dari bintang Urutan Utama ke Red Giants.
Cepheid terdiri dari 3 tipe: Tipe-I, Tipe-II, RR-Lyrae dengan urutan periode pulsasi yang menurun.
Periode berdenyut Cepheid berbanding lurus dengan kecerahannya (luminositas).
Pengamatan Hubble memanfaatkan fakta bahwa kecepatan radial terkait dengan pergeseran Spectral Lines. Di sini, kita akan mengamati empat kasus dan menemukan hubungan antara Kecepatan Recessional ($v_r$) dan Red Shift (z).
Kasus 1: Kasus Non-Relativistik Pemindahan Sumber
Dalam kasus ini, v jauh lebih kecil dari c. Sumber memancarkan beberapa sinyal (suara, cahaya, dll.), Yang disebarkan sebagaiWavefronts. Interval waktu antara pengiriman dua sinyal berturut-turut dalam bingkai sumber adalahΔts. Interval waktu antara penerimaan dua sinyal yang berurutan dalam bingkai pengamat adalahΔto.

Jika pengamat dan sumber tidak bergerak, maka Δts = Δto, tetapi ini tidak terjadi di sini. Sebaliknya, hubungannya adalah sebagai berikut.
$$\Delta t_o = \Delta t_s + \frac{\Delta l}{c}$$
Sekarang, $\Delta l = v \Delta t_s$
Juga, karena (kecepatan gelombang x waktu) = panjang gelombang, kita dapatkan
$$\frac{\Delta t_o}{\Delta t_s} = \frac{\lambda_o}{\lambda_s}$$
Dari persamaan di atas, kita mendapatkan hubungan berikut -
$$\frac{\lambda_o}{\lambda_s} = 1 + \frac{v}{c}$$
dimana $\lambda _s$ adalah panjang gelombang sinyal pada sumber dan $\lambda _o$ adalah panjang gelombang sinyal yang diinterpretasikan oleh pengamat.
Di sini, karena sumber menjauh dari pengamat, v positif.
Pergeseran merah -
$$z = \frac{\lambda_o - \lambda_s}{\lambda_s} = \frac{\lambda_o}{\lambda_s} - 1$$
Dari persamaan di atas, kita mendapatkan pergeseran Merah sebagai berikut.
$$z = \frac{v}{c}$$
Kasus 2: Kasus Non-Relativistik Pemindahan Pengamat
Dalam kasus ini, v jauh lebih kecil dari c. Sini,$\Delta l$ berbeda.
$$\Delta l = v \Delta t_o$$

Pada penyederhanaan, kami mendapatkan -
$$\frac{\Delta t_o}{\Delta t_s} = \left ( 1 - \frac{v}{c} \right )^{-1}$$
Kami mendapatkan shift Merah sebagai berikut -
$$z = \frac{v/c}{1-v/c}$$
Sejak v << c, ekspresi pergeseran merah untuk Kasus I dan Kasus II kira-kira sama.
Mari kita lihat bagaimana pergeseran merah yang diperoleh dalam dua kasus di atas berbeda.
$$z_{II} - z_I = \frac{v}{c} \left [ \frac{1}{1 - v/c}-1 \right ]$$
Karenanya, $z_{II} − z_{I}$ adalah angka yang sangat kecil karena $(v/c)^2$ faktor.
Ini menyiratkan bahwa, jika v << c, kita tidak dapat membedakan apakah sumber bergerak, atau pengamat bergerak.
Mari kita sekarang memahami Basics of STR (Teori Relativitas Khusus) -
Kecepatan cahaya adalah sebuah konstanta.
Ketika sumber (atau pengamat) bergerak dengan kecepatan yang sebanding dengan kecepatan cahaya, efek relativistik diamati.
Pelebaran waktu: $\Delta t_o = \gamma \Delta t_s$
Kontraksi panjang: $\Delta l_o = \Delta t_s/\gamma$
Sini, $\gamma$ adalah Lorrentz factor, lebih besar dari 1.
$$\gamma = \frac{1}{\sqrt{1-(v^2/c^2)}}$$
Kasus 3: Kasus Relativistik Pemindahan Sumber
Dalam hal ini, v sebanding dengan c. Mengacu pada gambar yang sama seperti pada Kasus I. Karena efek relativistik, dilatasi waktu diamati dan dengan demikian diperoleh hubungan berikut. (Sumber bergerak dengan kecepatan relativistik)
$$\Delta t_o = \gamma \Delta t_s + \frac{\Delta l}{c}$$
$$\Delta l = \frac{v\gamma \Delta t_s}{c}$$
$$\frac{\Delta t_o}{\Delta t_s} = \frac{1 + v/c}{\sqrt{1- (v^2/c^2)}}$$
Pada penyederhanaan lebih lanjut, kami mendapatkan,
$$1 + z = \sqrt{\frac{1+v/c}{1-v/c}}$$
Ekspresi di atas dikenal sebagai Kinematic Doppler Shift Expression.
Kasus 4: Kasus Relativistik Pemindahan Pengamat
Lihat gambar yang sama seperti pada Kasus II. Karena efek relativistik, pemendekan waktu diamati dan karenanya hubungan berikut diperoleh. (Pengamat bergerak dengan kecepatan relativistik)
$$\Delta t_o = \frac{\Delta t_s}{\gamma}+\frac{\Delta l}{c}$$
$$\Delta l = \frac{v\Delta t_o}{c}$$
$$\frac{\Delta t_o}{\Delta t_s} = \frac{\sqrt{1-( v^2/c^2)}}{1-v/c}$$
Pada penyederhanaan lebih lanjut, kami mendapatkan -
$$1 + z = \sqrt{\frac{1+ v/c}{1- v/c}}$$
Ekspresi di atas sama dengan yang kita dapatkan untuk Kasus III.
Poin untuk Diingat
Kecepatan resesi dan pergeseran merah sebuah bintang adalah besaran yang terkait.
Dalam kasus non-relativistik, kita tidak dapat menentukan apakah sumbernya bergerak atau diam.
Dalam kasus relativistik, tidak ada perbedaan dalam hubungan kecepatan resesi-pergeseran merah untuk sumber atau pengamat yang bergerak.
Jam bergerak yang bergerak lebih lambat, merupakan akibat langsung dari teori relativitas.
Sebuah galaksi yang bergeser merah z = 10, sesuai dengan v≈80% dari c. Massa Bima Sakti ada di sekitar1011M⊙, jika kita mempertimbangkan materi gelap, itu dia 1012M⊙. Bima Sakti kita begitu masif. Jika bergerak pada 80%c, ini tidak sesuai dengan konsep umum tentang bagaimana benda bergerak.
Kita tahu,
$$\frac{v_r}{c} = \frac{\lambda_{obs} - \lambda{rest}}{\lambda_{rest}}$$
Untuk nilai z kecil,
$$z = \frac{v_r}{c} = \frac{\lambda_{obs}-\lambda_{rest}}{\lambda_{rest}}$$
Pada grafik berikut, kelas antara fluks dan panjang gelombang, terdapat garis emisi di atas kontinum. DariH-α informasi baris, kita dapat menyimpulkan bahwa secara kasar z = 7. Ini menyiratkan galaksi bergerak pada 70%c. Kami mengamati pergeseran dan menafsirkannya sebagai kecepatan. Kita harus menyingkirkan gagasan ini dan melihatzdengan cara yang berbeda. Bayangkan ruang sebagai kisi 2D yang mewakili alam semesta seperti yang ditunjukkan di bawah ini.

Anggaplah bintang hitam adalah bima sakti kita dan bintang biru adalah galaksi lain. Ketika kita merekam cahaya dari galaksi ini, kita melihat spektrumnya dan mengetahui pergeseran merahnya, yaitu galaksi sedang bergerak menjauh. Ketika foton dipancarkan, ia memiliki kecepatan relatif.
Bagaimana jika ruangnya meluas?
Ini adalah pergeseran merah foton secara instan. Pergeseran merah kumulatif di sepanjang ruang antara dua galaksi akan cenderung menjadi pergeseran merah yang besar. Panjang gelombang akhirnya akan berubah. Ini adalah perluasan ruang dan bukan gerakan kinematik galaksi.
Gambar berikut menunjukkan jika gravitasi timbal balik meluap ekspansi maka ini tidak berpartisipasi dalam hukum Hubble.

Dalam Pergeseran Doppler Kinematik, pergeseran merah diinduksi dalam foton pada saat emisi. Dalam Pergeseran Merah Kosmologis, di setiap langkah, pergeseran merah secara kumulatif. Dalam potensial gravitasi, foton akan bergeser menjadi biru. Saat merangkak keluar dari potensi gravitasi, ia mengalami pergeseran merah.
Menurut Teori Relativitas Khusus, dua benda yang melewati satu sama lain tidak dapat memiliki kecepatan relatif lebih besar dari kecepatan cahaya. Kecepatan yang kita bicarakan adalah perluasan alam semesta. Untuk nilai z yang besar, pergeseran merah bersifat kosmologis dan bukan ukuran yang valid dari kecepatan resesi aktual objek terhadap kita.
Prinsip Kosmologis
Itu berasal dari Copernicus Notionalam semesta. Sesuai dengan gagasan ini, alam semesta bersifat homogen dan isotropik. Tidak ada arah dan lokasi yang disukai di alam semesta.
Homogenitas berarti tidak peduli di bagian mana Anda tinggal, Anda akan melihat alam semesta sama di semua bagian. Sifat isotropik berarti ke mana pun Anda melihat, Anda akan melihat struktur yang sama.
Contoh yang cocok untuk homogenitas adalah Sawah. Terlihat homogen dari semua bagian, namun pada saat angin mengalir terdapat variasi orientasinya sehingga tidak isotropik. Bayangkan sebuah gunung di atas tanah datar dan seorang pengamat sedang berdiri di puncak gunung. Dia akan melihat sifat isotropik dari tanah datar, tetapi tidak homogen. Jika di alam semesta homogen, ia isotropik pada satu titik, ia isotropik di mana-mana.
Ada survei skala besar untuk memetakan alam semesta. Sloan Digital Sky Surveyadalah salah satu survei tersebut, yang tidak banyak berfokus pada deklinasi, tetapi pada kenaikan yang tepat. Waktu lihat balik sekitar 2 miliar tahun. Setiap piksel sesuai dengan lokasi galaksi dan warnanya sesuai dengan struktur morfologi. Warna hijau mewakili galaksi spiral biru sedangkan warna semu merah menunjukkan galaksi masif.
Galaksi berada dalam struktur berserabut dalam jaringan kosmologis dan terdapat celah di antara galaksi.
$\delta M/M \cong 1$yaitu fluktuasi distribusi massa adalah 1 M adalah massa materi yang ada di dalam kubus tertentu. Dalam hal ini, ambil kubus volume 50 Mpc.
Untuk sisi kubus 1000 Mpc, $\delta M/M \cong 10^{−4}$.
Salah satu cara untuk mengukur homogenitas adalah dengan mengambil fluktuasi massa. Fluktuasi massa akan lebih tinggi pada skala yang lebih rendah.
Untuk mengukur sifat isotropik, pertimbangkan radiasi latar gelombang mikro kosmik. Alam semesta hampir isotropik pada skala sudut yang besar.
Poin untuk Diingat
Dua benda yang lewat satu sama lain tidak dapat memiliki kecepatan relatif lebih besar dari kecepatan cahaya.
Prinsip Kosmologis menyatakan bahwa alam semesta itu homogen dan isotropik.
Homogenitas ini ada pada skala sudut yang sangat besar dan bukan pada skala yang lebih kecil.
SDSS (Sloan Digital Sky Survey) adalah upaya untuk memetakan langit malam dengan memverifikasi Prinsip Kosmologis.
Sesuai dengan hukum kekekalan energi dan hukum kekekalan massa, jumlah total energi termasuk massa (E = mc 2 ) tetap tidak berubah sepanjang setiap langkah dalam proses apapun di alam semesta. Ekspansi alam semesta itu sendiri memakan energi yang mungkin dari peregangan panjang gelombang foton (Pergeseran Merah Kosmologis), Interaksi Energi Gelap, dll.
Untuk mempercepat survei lebih dari 26.000 galaksi, Stephen A. Shectmanmerancang alat yang mampu mengukur 112 galaksi secara bersamaan. Di pelat logam, lubang yang sesuai dengan posisi galaksi di langit dibor. Kabel serat optik membawa cahaya dari setiap galaksi ke saluran terpisah pada spektograf di teleskop du Pont 2,5 meter diCarnegie Observatories di Cerro Las Campanas di Chili.
Untuk efisiensi maksimum, teknik khusus yang dikenal sebagai Drift-Scan Photometrydigunakan, di mana teleskop diarahkan ke awal bidang survei dan kemudian penggerak otomatis dimatikan. Teleskop itu berdiri diam saat langit berlalu. Komputer membaca informasi dariCCD Detectorpada tingkat yang sama dengan rotasi bumi, menghasilkan satu gambar yang panjang dan terus menerus pada garis lintang langit yang konstan. Menyelesaikan fotometri memakan waktu total 450 jam.
Ada berbagai bentuk kebisingan dan pemodelan matematisnya berbeda tergantung pada propertinya. Berbagai proses fisik mengembangkan spektrum kekuatan alam semesta dalam skala besar. Spektrum daya awal yang diberikan karena fluktuasi kuantum mengikuti frekuensi pangkat ketiga negatif yang merupakan bentukPink Noise Spectrum dalam tiga dimensi.
Metrik
Dalam kosmologi, seseorang harus terlebih dahulu memiliki definisi ruang. Metrik adalah ekspresi matematika yang mendeskripsikan titik dalam ruang. Pengamatan langit dilakukan dalam geometri bola; karenanya sistem koordinat bola harus digunakan. Jarak antara dua titik yang berjarak dekat diberikan oleh -
$$ds^2 = dr^2 + r^2\theta ^2 + r^2 sin^2\theta d\phi^2$$
Gambar berikut menunjukkan Geometri di ruang Euclidean 3 dimensi yang tidak meluas.

Geometri ini masih dalam ruang Euclidean 3 dimensi yang tidak mengembang. Karenanya, grid referensi yang mendefinisikan frame itu sendiri akan meluas. Gambar berikut menggambarkan peningkatan metrik.

Faktor skala dimasukkan ke dalam persamaan ruang tak-mengembang, yang disebut 'faktor skala' yang menggabungkan pemuaian alam semesta dengan waktu.
$$ds^2 = a^2(t)\left [ dr^2 + r^2\theta^2 + r^2 sin^2\theta d\phi^2 \right ]$$
dimana a(t) adalah faktor skala, terkadang ditulis sebagai R(t). Sedangkan,a(t) > 1 berarti perbesaran metrik, sedangkan a(t) < 1 berarti penyusutan metrik dan a(t) = 1berarti metrik konstan. Sebagai konvensi,a(t0) = 1.
Sistem Koordinat Comoving
Di sebuah Comoving Coordinate System, skala pengukuran mengembang seiring dengan kerangka (alam semesta mengembang).
Di sini $\left [ dr^2 + r^2\theta^2 + r^2 sin^2\theta d\phi^2 \right ]$ adalah Comoving Distance, dan $ds^2$ adalah jarak yang tepat.
Jarak yang tepat akan sesuai dengan jarak sebenarnya yang diukur dari galaksi jauh dari bumi pada saat pengamatan, alias jarak benda sesaat.
Ini karena jarak yang ditempuh oleh foton ketika mencapai pengamat dari sumber yang jauh akan menjadi yang diterima $t=t_0$ dari pengamat, yang berarti bahwa jarak pengamatan sesaat akan menjadi jarak yang tepat, dan seseorang dapat memprediksi jarak masa depan dengan menggunakan faktor laju dan panjang terukur awal sebagai referensi.
Konsep Comoving dan jarak yang tepat penting dalam mengukur nilai sebenarnya dari jumlah massa jenis galaksi dalam volume tertentu ruang yang diamati. Seseorang harus menggunakan jarak Comoving untuk menghitung kerapatan pada saat pembentukannya ketika foton yang diamati dipancarkan. Itu bisa diperoleh setelah laju perluasan alam semesta dapat diperkirakan.
Untuk memperkirakan laju ekspansi, seseorang dapat mengamati perubahan jarak galaksi jauh yang diamati selama periode waktu yang lama.
Poin untuk Diingat
Metrik adalah ekspresi matematika yang menggambarkan titik-titik dalam ruang.
Faktor skala menentukan apakah alam semesta berkontraksi atau mengembang.
Dalam sistem koordinat bergerak, skala pengukuran mengembang bersama kerangka (alam semesta mengembang).
Jarak yang tepat adalah jarak sesaat benda.
Jarak tempuh adalah jarak benda sebenarnya.
Pada bab ini, kita akan memahami secara detail tentang Metrik Robertson-Walker.
Model untuk Faktor Skala Berubah dengan Waktu
Misalkan foton dipancarkan dari galaksi yang jauh. Ruang maju untuk foton ke segala arah. Ekspansi alam semesta ke segala arah. Mari kita lihat bagaimana faktor skala berubah seiring waktu dalam langkah-langkah berikut.
Step 1 - Untuk alam semesta statis, faktor skalanya adalah 1, yaitu nilai jarak comoving adalah jarak antar benda.
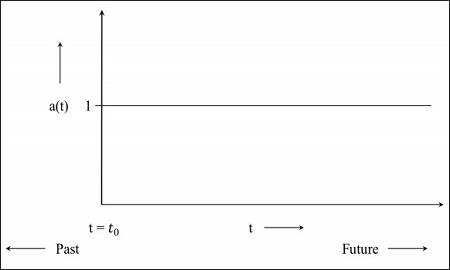
Step 2- Gambar berikut adalah grafik alam semesta yang masih mengembang tetapi dengan laju yang semakin berkurang, yang artinya grafik tersebut akan dimulai di masa lalu. Itut = 0 menunjukkan bahwa alam semesta dimulai dari titik itu.

Step 3 - Gambar berikut adalah grafik alam semesta yang mengembang dengan kecepatan yang lebih cepat.

Step 4 - Gambar berikut adalah grafik alam semesta yang mulai berkontraksi dari sekarang.

Jika nilai faktor skala menjadi 0 selama kontraksi alam semesta, itu menyiratkan jarak antara objek menjadi 0, yaitu jarak yang tepat menjadi 0. Jarak tempuh yang merupakan jarak antara benda-benda di alam semesta saat ini, adalah besaran yang konstan. Di masa depan, saat faktor skala menjadi0, semuanya akan semakin dekat. Modelnya bergantung pada komponen alam semesta.
Metrik untuk datar (Euclidean: tidak ada parameter untuk kelengkungan) alam semesta mengembang diberikan sebagai -
$$ds^2 = a^2(t)\left ( dr^2+r^2d\theta^2+r^2sin^2\theta d\varphi^2 \right )$$
Untuk ruang-waktu, elemen garis yang kita peroleh pada persamaan di atas dimodifikasi sebagai -
$$ds^2 = c^2dt^2 - \left \{ a^2(t) \left ( dr^2 + r^2d\theta ^2 + r^2sin^2\theta d\varphi^2 \right ) \right \}$$
Untuk ruang-waktu, waktu saat foton dipancarkan dan saat dideteksi berbeda. Jarak yang tepat adalah jarak sesaat ke objek yang dapat berubah seiring waktu karena perluasan alam semesta. Ini adalah jarak yang ditempuh foton dari objek yang berbeda untuk mencapai kita. Ini terkait dengan jarak tempuh sebagai -
$$d_p = a(t) \times d_c$$
dimana $d_p$ adalah jarak yang tepat dan $d_c$ adalah jarak comoving, yang tetap.
Jarak yang diukur ke benda-benda di alam semesta saat ini diambil sebagai jarak bergerak, yang berarti jarak bergerak tetap dan tidak berubah oleh ekspansi. Dahulu, faktor skala lebih kecil dari 1, yang menunjukkan bahwa jarak yang tepat lebih kecil.
Kita bisa mengukur pergeseran merah ke galaksi. Karenanya jarak yang tepat$d_p$ sesuai dengan $c \times t(z)$, dimana $t(z)$adalah waktu lookback menuju pergeseran merah dan c adalah kecepatan cahaya dalam ruang hampa. Waktu lihat balik adalah fungsi dari pergeseran merah(z).
Berdasarkan pengertian di atas, mari kita analisis bagaimana pergeseran merah kosmologis diinterpretasikan dalam skenario ini $d_p = a(t) \times d_c$.
Asumsikan foton (yang terikat dengan bumi) dipancarkan oleh galaksi, G. The $t_{em}$ sesuai dengan waktu ketika foton dipancarkan; $a(t_{em})$adalah faktor skala pada saat foton itu dipancarkan. Pada saat mendeteksi foton, seluruh alam semesta telah mengembang, yaitu foton bergeser merah pada saat pendeteksian. Itu$t_{obs}$ sesuai dengan waktu ketika foton terdeteksi dan faktor skala yang sesuai adalah $a(t_{obs})$.
Faktor pertumbuhan alam semesta diberikan oleh -
$$\frac{a(t_{obs})}{a(t_{em})}$$
Faktor yang memuai panjang gelombang adalah -
$$\frac{\lambda_{obs}}{\lambda_{em}}$$
yang sama dengan faktor pertumbuhan alam semesta. Simbol memiliki arti yang biasa. Karena itu,
$$\frac{a(t_{obs})}{a(t_{em})} = \frac{\lambda_{obs}}{\lambda_{em}}$$
Kami tahu pergeseran merah itu (z) adalah -
$$z=\frac{\lambda_{obs} - \lambda_{em}}{\lambda_{em}} = \frac{\lambda_{obs}}{\lambda_{em}} - 1$$
$$1 + z = \frac{a(t_{obs})}{a(t_{em})}$$
Nilai sekarang dari faktor skala adalah 1, karenanya $a(t_{obs}) = 1$ dan menunjukkan faktor skala saat foton dipancarkan di masa lalu oleh $a(t)$.
Karena itu,
$$1 + z = \frac{1}{a(t)}$$
Interpretasi Redshift dalam Kosmologi
Untuk memahami ini, mari kita ambil contoh berikut: Jika $z = 2$ kemudian $a(t) = 1/3$.
Ini menyiratkan bahwa alam semesta telah mengembang dengan faktor tiga sejak cahaya meninggalkan objek itu. Panjang gelombang radiasi yang diterima telah meluas dengan faktor tiga karena ruang angkasa telah mengembang dengan faktor yang sama selama transit dari objek yang memancarkannya. Perlu dicatat bahwa pada nilai yang begitu besarz, pergeseran merah terutama pergeseran merah kosmologis, dan ini bukan ukuran yang valid dari kecepatan resesi aktual objek terhadap kita.
Untuk latar belakang gelombang mikro kosmik (CMB), z = 1089, yang berarti bahwa alam semesta saat ini telah mengembang dengan faktor ∼1090. Metrik untuk alam semesta datar, Euclidean, mengembang diberikan sebagai -
$$ds^2 = a^2(t)(dr^2 + r^2d\theta^2 + r^2sin^2\theta d\varphi^2)$$
Kami ingin menulis metrik dalam kelengkungan apa pun.
Robertson and Walker terbukti untuk setiap alam semesta kelengkungan (yang homogen dan isotropik), metrik diberikan sebagai -
$$ds^2 = a^2(t) \left [ \frac{dr^2}{1-kr^2} + r^2d\theta^2 + r^2sin^2\theta d\varphi^2 \right ]$$
Ini umumnya dikenal sebagai file Robertson–Walker Metricdan berlaku untuk topologi ruang apa pun. Harap perhatikan faktor tambahan dalam$dr^2$. Sini adalah konstanta kelengkungan.
Geometri Alam Semesta
Geometri Alam Semesta dijelaskan dengan bantuan Lengkungan berikut, yang meliputi -
- Lengkungan Positif
- Lengkungan Negatif
- Lengkungan Nol
Mari kita pahami masing-masing secara rinci.
Lengkungan Positif
Jika bidang singgung yang digambar pada suatu titik pada permukaan kelengkungan tidak berpotongan pada titik mana pun di permukaan, hal itu disebut permukaan dengan kelengkungan positif yaitu permukaan tetap pada satu sisi bidang singgung pada titik tersebut. Permukaan bola memiliki kelengkungan positif.
Lengkungan Negatif
Jika bidang singgung yang digambar pada suatu titik pada permukaan kelengkungan berpotongan pada titik mana pun di permukaan, hal itu disebut permukaan dengan kelengkungan negatif, yaitu kurva permukaan menjauhi bidang singgung dalam dua arah yang berbeda. Permukaan berbentuk pelana memiliki kelengkungan negatif.
Sekarang perhatikan permukaan bola. Jika sebuah segitiga dibangun di atas permukaan bola dengan menggabungkan tiga titik dengan geodesik (busur lingkaran besar), jumlah sudut interior segitiga bola tersebut lebih besar dari 180 o , yaitu -
$$\alpha + \beta + \gamma > \pi$$
Ruang seperti itu disebut ruang lengkung positif. Juga, kelengkungannya homogen dan isotropik. Secara umum, sudut pada simpul dari segitiga bulat mengikuti hubungan -
$$\alpha + \beta +\gamma = \pi + A/R^2$$
dimana A adalah luas segitiga dan Radalah jari-jari bola. Gambar berikut menggambarkan ruang yang melengkung secara positif.

Untuk kelengkungan positif, garis sejajar harus bertemu. Pertimbangkan permukaan bumi, yang merupakan ruang melengkung positif. Ambil dua titik awal di ekuator. Garis-garis yang melintasi ekuator pada sudut siku-siku dikenal sebagai garis bujur. Karena garis-garis ini melintasi ekuator dengan sudut siku-siku, garis-garis ini dapat disebut garis sejajar. Dimulai dari ekuator, mereka akhirnya berpotongan di kutub. Metode ini digunakan olehCarl Gauss dan lainnya untuk memahami topologi bumi.
Pertimbangkan ruang melengkung negatif (sadel ditunjukkan pada gambar berikut), jumlah sudut interior segitiga kurang dari 180 o , yaitu -
$$\alpha + \beta + \gamma < \pi$$
Sudut pada simpul mengikuti relasi -
$$\alpha + \beta + \gamma = \pi - A/R^2$$

Lengkungan Nol
Permukaan bidang memiliki kelengkungan nol. Sekarang untuk ruang datar, jika sebuah bidang diambil dan sebuah segitiga dibangun dengan menggabungkan tiga titik dengan geodesik (garis lurus), jumlah sudut interiornya adalah -
$$\alpha + \beta + \gamma = \pi$$
Gambar berikut adalah ruang 2 dimensi datar.

Jika seseorang ingin suatu ruang menjadi homogen dan isotropik, hanya tiga kemungkinan yang tersisa: ruang tersebut dapat datar secara seragam atau dapat memiliki kelengkungan positif yang seragam atau dapat memiliki kelengkungan negatif yang seragam.
Konstanta kelengkungan dapat mengasumsikan salah satu dari tiga nilai berikut.
$$k = \begin{cases}+1, & for \: a\: positively \: curved\: space;\\\quad 0, & for\: a \: flat \: space;\\-1, & for\: a \: negatively \: curved \: space;\end{cases}$$
Topologi Global Semesta
Alam semesta memiliki topologi tertentu, tetapi secara lokal dapat memiliki kerutan. Bergantung pada bagaimana materi didistribusikan di dalam ruang, ada variasi yang lebih kecil dalam kelengkungannya. Mari kita asumsikan bahwa ada sebuah kelas benda yang memiliki ukuran sebenarnya yang sama di mana pun ia berada di alam semesta, yang artinya mereka seperti lilin standar. Mereka tidak memiliki kecerahan yang sama, tetapi mereka memiliki ukuran yang sama.
Jika objek berada dalam ruang melengkung positif dan foton berasal dari titik A (salah satu ujung objek) dan B (ujung objek lainnya), foton akan merambat secara paralel dalam ruang melengkung positif melalui jalur geodesik dan akhirnya akan bertemu . Bagi seorang pengamat di C, akan terlihat bahwa itu berasal dari dua titik berbeda dengan arah yang berbeda.
Jika benda tersebut berada di alam semesta lokal dan kita ukur ukuran sudutnya, tidak terpengaruh oleh kelengkungan tersebut. Jika kelas objek yang sama terlihat pada pergeseran merah yang lebih besar, ukuran sudut tidak berkorelasi dengannya.
$$\theta = \frac{d}{r}$$
Dimana d adalah ukuran objek dan radalah jarak ke benda, yaitu jika ukurannya lebih besar dari ukuran setempat, berarti kelengkungannya positif. Gambar berikut adalah representasi dari foton yang terdeteksi dalam ruang yang melengkung secara positif.

Perlu dicatat bahwa tidak ada objek astrofisika nyata yang berukuran dan morfologi standar. Meskipun cD elips besar - galaksi dianggap sesuai dengan lilin standar, tetapi mereka juga ditemukan berevolusi seiring waktu.
Menemukan Jarak ke Galaksi
Pada bagian ini, kita akan membahas cara mencari jarak ke suatu galaksi dengan memperhatikan gambar berikut.

Pertimbangkan Bima Sakti di (r, θ,) dalam kerangka istirahat kosmologis. Satu dapat mengambil = 0; (0, θ, ϕ), yaitu pusat alam semesta dengan menggunakan asumsi homogenitas.
Pertimbangkan galaksi 'G' di (r1, θ,). Jarak (tepat) adalah jarak radial terpendek yang ditempuh oleh foton. Dari kesimetrian ruang - waktu, geodesik nol dari r = 0 hingga r = r1, memiliki arah konstan dalam ruang. Dalam propagasi radialnya, koordinat sudut tidak berubah. Jika koordinat sudut berubah, maka itu bukan jalur terpendek. Itulah alasan mengapa istilah kelengkungan ada di dr 2 .
Poin untuk Diingat
Ekspansi alam semesta ke segala arah.
Alam semesta bisa statis, mengembang atau menyusut tergantung pada evolusi faktor skala.
Galaksi cD berkembang seiring waktu dan karenanya tidak dapat digunakan sebagai candle standar.
Alam semesta memiliki topologi tertentu, tetapi secara lokal dapat memiliki kerutan.
Pada bab ini, kita akan membahas tentang Parameter Hubble serta Faktor Skala.
Prerequisite - Pergeseran Merah Kosmologis, Prinsip Kosmologis.
Assumption - Alam semesta itu homogen dan isotropik.
Konstanta Hubble dengan Fractional Rate of Change of Scale Factor
Pada bagian ini, kita akan menghubungkan Konstanta Hubble dengan laju pecahan Faktor Skala Perubahan.
Kecepatan dapat dituliskan dengan cara berikut dan disederhanakan.
$$v = \frac{\mathrm{d} r_p}{\mathrm{d} t}$$
$$= \frac{d[a(t)r_c}{dt}$$
$$v = \frac{\mathrm{d} a}{\mathrm{d} t} \ast \frac{1}{a} \ast (ar_c)$$
$$v = \frac{\mathrm{d} a}{\mathrm{d} t} \ast \frac{1}{a} \ast r_p$$
Sini, v adalah kecepatan resesi, a adalah faktor skala dan rp adalah jarak yang tepat antar galaksi.
Hubble’s Empirical Formula adalah dari alam -
$$v = H \ast r_p$$
Jadi, membandingkan dua persamaan di atas yang kita peroleh -
Hubble’s Parameter = Fractional rate of change of the scale factor
$$H = da/dt \ast 1/a$$
Note- Ini bukan konstanta karena faktor skala adalah fungsi waktu. Karenanya ini disebut parameter Hubble dan bukan konstanta Hubble.
Secara empiris kami menulis -
$$H = V/D$$
Jadi, dari persamaan ini, kita dapat menyimpulkan bahwa sejak D meningkat dan V adalah konstanta H berkurang seiring waktu dan perluasan alam semesta.
Persamaan Friedmann dalam Hubungannya dengan Model Robertson-Walker
Pada bagian ini, kita akan memahami bagaimana Persamaan Friedmann digunakan dalam hubungannya dengan model Robertson-Walker. Untuk memahami ini, mari kita ambil gambar berikut yang memiliki massa uji pada jarakrp dari tubuh massa M sebagai contoh.

Mempertimbangkan gambar di atas, kita dapat mengekspresikan gaya sebagai -
$$F = G \ast M \ast \frac{m}{r^2_p}$$
Sini, G adalah konstanta gravitasi universal dan ρ adalah kerapatan materi di dalam alam semesta teramati.
Sekarang, dengan asumsi kerapatan massa seragam dalam bola kita dapat menulis -
$$M = \frac{4}{3} \ast \pi \ast r_p^3 \ast \rho$$
Menggunakan ini kembali dalam persamaan gaya kita, kita dapatkan -
$$F = \frac{4}{3} \ast \pi \ast G \ast r_p \ast \rho \ast m$$
Jadi, kita dapat menuliskan energi potensial dan energi kinetik dari massa tersebut m sebagai -
$$V = -\frac{4}{3} \ast \pi \ast G \ast r^2_p \ast m \ast \rho$$
$$K.E = \frac{1}{2} \ast m \ast \frac{\mathrm{d} r_p^2}{\mathrm{d} t}$$
Menggunakan Virial Theorem -
$$U = K.E + V$$
$$U = \frac{1}{2} \ast m \ast \left ( \frac{\mathrm{d} r_p}{\mathrm{d} t} \right )^2 - \frac{4}{3} \ast \pi \ast G \ast r_p^2 \ast m \ast \rho$$
Tapi di sini, $r_p = ar_c$. Jadi, kami mendapatkan -
$$U = \frac{1}{2} \ast m \ast \left ( \frac{\mathrm{d} a}{\mathrm{d} t} \right )^2 r_c^2 - \frac{4}{3} \ast \pi \ast G \ast r_p^2 \ast m \ast \rho$$
Pada penyederhanaan lebih lanjut, kita mendapatkan persamaan Friedmann,
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi}{3} \ast G \ast \rho + \frac{2U}{m} \ast r_c^2 \ast a^2$$
Sini Uadalah sebuah konstanta. Kami juga mencatat bahwa alam semesta tempat kita tinggal saat ini didominasi oleh materi, sedangkan kepadatan energi radiasinya sangat rendah.
Poin untuk Diingat
Parameter Hubble berkurang seiring waktu dan perluasan alam semesta.
Alam semesta tempat kita tinggal saat ini didominasi oleh materi dan kerapatan energi radiasi sangat rendah.
Dalam bab ini, kita akan memahami apa itu Persamaan Friedmann dan mempelajari secara rinci tentang Model Dunia untuk konstanta kelengkungan yang berbeda.
Persamaan Friedmann
Persamaan ini memberi tahu kita tentang perluasan ruang dalam model alam semesta homogen dan isotropik.
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho + \frac{2U}{mr_c^2a^2}$$
Ini telah diubah dalam konteks General Relativity (GR) dan Robertson-Walker Metric sebagai berikut.
Menggunakan persamaan GR -
$$\frac{2U}{mr_c^2} = -kc^2$$
Dimana kadalah konstanta kelengkungan. Karena itu,
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8 \pi G}{3}\rho - \frac{kc^2}{a^2}$$
Juga, $\rho$digantikan oleh kepadatan energi yang meliputi materi, radiasi, dan bentuk energi lainnya. Tetapi untuk tujuan representasi, itu ditulis sebagai$\rho$.
Model Dunia untuk Konstanta Kelengkungan yang Berbeda
Sekarang mari kita lihat berbagai kemungkinan tergantung pada nilai konstanta kelengkungan.
Kasus 1: k = 1, atau Alam Semesta Tertutup
Untuk alam semesta yang mengembang, $da/dt > 0$. Saat ekspansi berlanjut, suku pertama di kanan persamaan di atas adalah sebagai$a^{-3}$, sedangkan istilah kedua pergi sebagai $a^{-2}$. Ketika dua suku menjadi sama, alam semesta menghentikan ekspansi. Lalu -
$$\frac{8 \pi G}{3}\rho = \frac{kc^2}{a^2}$$
Di sini, k = 1, oleh karena itu,
$$a = \left [ \frac{3c^2}{8 \pi G\rho} \right ]^{\frac{1}{2}}$$
Alam semesta seperti itu terbatas dan memiliki volume yang terbatas. Ini disebut Semesta Tertutup.
Kasus 2: k = -1, atau Open Universe
Jika k < 0, ekspansi tidak akan pernah berhenti. Setelah beberapa saat, istilah pertama di kanan dapat diabaikan dibandingkan dengan istilah kedua.
Di sini, k = -1. Karena itu,$da/dt ∼ c$.
Dalam hal ini, alam semesta meluncur. Alam semesta seperti itu memiliki ruang dan waktu yang tidak terbatas. Ini disebut Alam Semesta Terbuka.
Kasus 3: k = 0, atau Alam Semesta Datar
Dalam kasus ini, alam semesta mengembang dengan laju yang semakin berkurang. Di sini, k = 0. Oleh karena itu,
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho$$
Alam semesta seperti itu memiliki ruang dan waktu yang tidak terbatas. Ini disebut Alam Semesta Datar.
Poin untuk Diingat
Persamaan Friedmann memberi tahu kita tentang perluasan ruang dalam model alam semesta homogen dan isotropik.
Bergantung pada nilai konstanta kelengkungan yang berbeda, kita dapat memiliki Semesta Tertutup, Terbuka atau Datar.
Dalam bab ini, kita akan membahas Persamaan Fluida dan bagaimana persamaan ini memberitahu kita tentang kepadatan alam semesta yang berubah seiring waktu.
Memperkirakan ρ c dan ρ di Alam Semesta Saat Ini
Untuk alam semesta saat ini -
$$\rho_c \simeq 10^{11}M_\odot M_{pc}^{-3} \simeq 10\: hydrogen \: atoms \: m^{-3}$$
Ada berbagai macam kepadatan kritis di luar angkasa kita. Seperti, untuk media intergalaksi$\rho_c$ adalah 1 atom hidrogen $m^{-3}$, sedangkan untuk awan molekul itu $10^6$ atom hidrogen $m^{−3}$.
Kita harus mengukur $\rho_c$mempertimbangkan sampel ruang yang tepat. Di dalam galaksi kita, nilai$\rho_c$sangat tinggi, tetapi galaksi kita bukanlah perwakilan dari seluruh alam semesta. Jadi, kita harus pergi ke luar angkasa di mana prinsip kosmologis berlaku, yaitu jarak ≈ 300 Mpc. Melihat 300 Mpc berarti melihat 1 miliar tahun yang lalu, tetapi tetaplah alam semesta saat ini.
Survei seperti SDSS dilakukan untuk menentukan kepadatan materi yang sebenarnya. Mereka mengambil volume 5 × 500 × 5 Mpc 3 , menghitung jumlah galaksi dan menambahkan semua cahaya yang datang dari galaksi-galaksi ini. Dengan asumsi bahwa 1 L ≡ 1 M, yaitu 1 Luminositas matahari ≡ 1 Massa matahari.
Kami melakukan konversi ringan ke massa dan kemudian kami mencoba memperkirakan jumlah baryon berdasarkan partikel materi terlihat yang ada dalam volume tersebut.
Sebagai contoh,
$$1000L_\odot ≡ 1000M_\odot / m_p$$
Dimana, m p = massa proton.
Kemudian kita mendapatkan secara kasar kepadatan bilangan baryon $\Omega b ∼= 0.025$. Ini menyiratkan$\rho b = 0.25%$ dari $\rho_c$. Survei yang berbeda menghasilkan nilai yang sedikit berbeda. Jadi, di alam semesta lokal, kepadatan jumlah materi yang terlihat jauh lebih sedikit daripada kepadatan kritis, artinya kita hidup di alam semesta terbuka.
Massa dengan faktor 10 tidak dimasukkan dalam survei ini karena survei ini memperhitungkan radiasi elektromagnetik tetapi bukan materi gelap. Memberi,$\Omega_m = 0.3 − 0.4$. Masih menyimpulkan bahwa kita hidup di alam semesta terbuka.
Materi gelap berinteraksi dengan gravitasi. Banyak materi gelap yang dapat menghentikan ekspansi. Kami belum meresmikan caranya$\rho$ berubah seiring waktu, yang karenanya kita membutuhkan kumpulan persamaan lain.
Termodinamika menyatakan bahwa -
$$dQ = dU + dW$$
Untuk sistem yang berkembang dalam hal ukuran, $dW = P dV$. Ekspansi alam semesta dimodelkan sebagai adiabatik yaitu$dQ = 0$. Jadi, perubahan volume harus terjadi dari perubahan dU energi internal.
Mari kita ambil volume alam semesta tertentu dari radius yang bergerak unit yaitu $r_c = 1$. Jika$\rho$ adalah kepadatan material dalam volume ruang ini, lalu,
$$M = \frac{4}{3} \pi a^3r_c^3 \rho$$
$$U = \frac{4}{3}\pi a^3\rho c^2$$
Dimana, Uadalah kepadatan Energi. Mari kita cari tahu perubahan energi internal seiring dengan waktu saat alam semesta berkembang.
$$\frac{\mathrm{d} U}{\mathrm{d} t} = 4 \pi a^2 \rho c^2 \frac{\mathrm{d} a}{\mathrm{d} t} + \frac{4}{3}\pi a^3 c^2\frac{\mathrm{d} \rho}{\mathrm{d} t}$$
Demikian pula, perubahan volume dengan waktu diberikan oleh,
$$\frac{\mathrm{d} V}{\mathrm{d} t} = 4\pi a^2 \frac{\mathrm{d} a}{\mathrm{d} t}$$
Mengganti $dU = −P dV$. Kita mendapatkan,
$$4\pi a^2(c^2 \rho +P)\dot{a}+\frac{4}{3}\pi a^3c^2\dot{\rho} = 0$$
$$\dot{\rho}+3\frac{\dot{a}}{a}\left ( \rho + \frac{P}{c^2} \right ) = 0$$
Ini disebut Fluid Equation. Ini memberi tahu kita bagaimana kepadatan alam semesta berubah seiring waktu.
Tekanan turun saat alam semesta mengembang. Pada setiap tekanan instan berubah, tetapi tidak ada perbedaan tekanan antara dua titik dalam volume yang dipertimbangkan, jadi gradien tekanan adalah nol. Hanya material relativistik yang memberikan tekanan, materi tidak memiliki tekanan.
Persamaan Friedmann bersama dengan Persamaan Fluida memodelkan alam semesta.
Poin untuk Diingat
Materi gelap berinteraksi dengan gravitasi. Banyak materi gelap yang dapat menghentikan ekspansi.
Persamaan Fluida memberi tahu kita bagaimana kepadatan alam semesta berubah seiring waktu.
Persamaan Friedmann bersama dengan Persamaan Fluida memodelkan alam semesta.
Hanya material relativistik yang memberikan tekanan, materi tidak memiliki tekanan.
Dalam bab ini, kita akan membahas Solusi Persamaan Friedmann yang berkaitan dengan Alam Semesta yang Didominasi Materi. Dalam kosmologi, karena kita melihat segala sesuatu dalam skala besar, tata surya, galaksi, segala sesuatu terjadi seperti partikel debu (itulah yang kita lihat dengan mata kita), kita bisa menyebutnya alam semesta berdebu atau alam semesta materi saja.
Dalam Fluid Equation,
$$\dot{\rho} = -3\left ( \frac{\dot{a}}{a} \right )\rho -3\left ( \frac{\dot{a}}{a} \right )\left ( \frac{P}{c^2} \right )$$
Kita bisa lihat ada istilah tekanan. Untuk alam semesta yang berdebu,P = 0, karena rapatan energi materi akan lebih besar dari tekanan radiasi, dan materi tidak bergerak dengan kecepatan relativistik.
Jadi, Persamaan Fluida akan menjadi,
$$\dot{\rho} = -3\left ( \frac{\dot{a}}{a} \right )\rho$$
$$\Rightarrow \dot{\rho}a + 3\dot{a}\rho = 0$$
$$\Rightarrow \frac{1}{a^3}\frac{\mathrm{d}}{\mathrm{d} t}(a^3 \rho) = 0$$
$$\Rightarrow \rho a^3 =\: constant$$
$$\Rightarrow \rho \propto \frac{1}{a^3}$$
Tidak ada intuisi lawan dalam persamaan ini karena kepadatan harus berskala $a^{-3}$ karena Volume meningkat sebagai $a^3$.
Dari hubungan terakhir, kita dapat mengatakan bahwa,
$$\frac{\rho (t)}{\rho_0} = \left [ \frac{a_0}{a(t)} \right ]^3$$
Untuk alam semesta saat ini, a, yang sama dengan a0 seharusnya 1. Jadi,
$$\rho(t) = \frac{\rho_0}{a^3}$$
Dalam materi yang didominasi alam semesta datar, k = 0. Jadi, persamaan Friedmann akan menjadi,
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8 \pi G\rho}{3}$$
$$\dot{a}^2 = \frac{8\pi G \rho a^2}{3}$$
Dengan menyelesaikan persamaan ini, kita akan mendapatkan,
$$a \propto t^{2/3}$$
$$\frac{a(t)}{a_0} = \left ( \frac{t}{t_0} \right )^{2/3}$$
$$a(t) = \left( \frac{t}{t_0} \right )^{2/3}$$
Artinya, alam semesta akan terus bertambah dengan laju yang semakin berkurang. Gambar berikut menunjukkan perluasan Dusty Universe.

Bagaimana ρ Berubah dengan Waktu?
Lihatlah persamaan berikut -
$$\frac{\rho(t)}{\rho_0} = \left ( \frac{t_0}{t} \right )^2$$
Kita tahu bahwa faktor skala berubah seiring dengan waktu $t^{2/3}$. Begitu,
$$a(t) = \left ( \frac{t}{t_0} \right )^{2/3}$$
Membedakannya, kita akan mendapatkan,
$$\frac{(da)}{dt} = \dot{a} = \frac{2}{3} \left ( \frac{t^{-1/3}}{t_0} \right )$$
Kami tahu bahwa Hubble Constant adalah,
$$H(t) = \frac{\dot{a}}{a} = \frac{2}{3t}$$
Ini adalah persamaan untuk Einstein-de sitter Universe. Jika kita ingin menghitung usia alam semesta saat ini,
$$t_0 = t_{age} = \frac{2}{3H_0}$$
Setelah memasukkan nilai $H_0$ untuk jagat raya sekarang, kita akan mendapatkan nilai umur jagat raya sebagai 9 Gyrs. Ada banyakGlobular Cluster di galaksi bima sakti kita yang usianya lebih dari itu.
Itu semua tentang alam semesta yang berdebu. Sekarang, jika Anda berasumsi bahwa alam semesta didominasi oleh radiasi dan bukan oleh materi, maka kerapatan energi radiasi berlaku sebagai$a^{-4}$ daripada $a^{-3}$. Kami akan melihat lebih banyak di bab berikutnya.
Poin untuk Diingat
Dalam kosmologi, segala sesuatu terjadi seperti partikel debu, oleh karena itu kita menyebutnya alam semesta berdebu atau alam semesta materi saja.
Jika kita berasumsi bahwa alam semesta didominasi oleh radiasi dan bukan oleh materi, maka kerapatan energi radiasi menjadi sama $a^{-4}$ daripada $a^{-3}$.
Dalam bab ini, kita akan membahas Solusi untuk Persamaan Friedmann yang berkaitan dengan Alam Semesta yang Didominasi Radiasi. Pada awalnya, kami membandingkan kepadatan energi materi dengan radiasi. Ini akan memungkinkan kita untuk melihat apakah alam semesta kita didominasi materi atau radiasi.
Kepadatan Energi Radiasi
Radiasi yang lazim di alam semesta saat ini dapat dikaitkan sangat sedikit dengan sumber bintang, tetapi ini terutama disebabkan oleh sisa CMB (Latar Belakang Gelombang Mikro Kosmik).
Kepadatan energi radiasi, $\epsilon_{\gamma,0}$, dapat diungkapkan sebagai berikut -
$$\epsilon_{\gamma,0} = aT_0^4$$
Sini, a adalah konstanta radiasi yang memiliki ekspresi $(8\pi^5k_B^4)/(15h^3c^2)$ sama dengan a = 7.5657 × 10−15erg\: cm−3 K−4. Suhu, T0, kami pertimbangkan di sini, sesuai dengan benda hitam yang berhubungan dengan CMB.
Mengganti hasil, kami punya,
$$\epsilon_{\gamma,0} = aT_0^4 = 4 \times 10^{-13}erg\: cm^{-3}$$
Kepadatan Energi Materi
Dalam kalkulasi berikut, kita memiliki asumsi bekerja dengan alam semesta datar dan K = 0. Kita menganggap kerapatan energi materi sebagai $\epsilon = \rho c^2$. Kami mempertimbangkan yang berikut -
$$\rho_{m,0}c^2 = 0.3\rho_{c,0}c^2 = 0.3 \times \frac{3H_0^2}{8\pi G} \times c^2$$
$$\rho_{m,0}c^2 \simeq 2 \times 10^{-8} erg \:cm^{-3}$$
$$\rho_{b,0}c^2 = 0.03\rho_{c,0}c^2 = 0.03 \times \frac{3H_0^2}{8\pi G} \times c^2$$
$$\rho_{b,0}c^2 \simeq 2 \times 10^{-9} erg\: cm^{-3}$$
Jadi, dari kalkulasi di atas, kita melihat bahwa kita hidup di alam semesta yang didominasi materi. Ini dapat didukung oleh fakta bahwa CMB sangat dingin. Saat kita melihat ke masa lalu, kita akan mendapati suhu CMB semakin panas, dan akan dapat menyimpulkan bahwa mungkin ada zaman di mana alam semesta didominasi oleh radiasi.
Variasi Faktor Massa Jenis dan Skala
Persamaan fluida menunjukkan kepada kita bahwa -
$$\dot{\rho} + 3\frac{\dot{a}}{a}\left ( \rho + \frac{P}{c^2} \right ) = 0$$
Jika kita menganggap alam semesta berdebu, kita akan mendapatkan P = 0. Mengesampingkan hasil sebelumnya, kita menganggap alam semesta didominasi oleh radiasi.
$$\dot{\rho}_{rad} + 3 \frac{\dot{a}}{a}\left ( \rho_{rad} + \frac{P}{c^2} \right ) = 0$$
Menggunakan hubungan tekanan $P_{rad} = \rho c^{2/3}$ kita punya -
$$\dot{\rho}_{rad} + 3 \frac{\dot{a}}{a}\left ( \rho_{rad} + \frac{\rho_{rad}}{3} \right ) = 0$$
$$\dot{\rho}_{rad} + 4\frac{\dot{a}}{a}(\rho_{rad}) = 0$$
Pada penyederhanaan lebih lanjut, kami memiliki,
$$\frac{1}{a^4}\frac{\mathrm{d}}{\mathrm{d} t}(\rho_{rad}a^4) = 0$$
$$\rho_{rad}a^4 =\: constant$$
$$\rho_{rad} \propto \frac{1}{a^4}$$
Di atas hasil menunjukkan terbalik 4 th variasi kekuatan dengan$\rho$.
Ini secara fisik dapat diartikan sebagai $a^{-3}$berasal dari variasi volume yang meningkat. Yang tersisa$a^{-1}$dapat diperlakukan sebagai energi yang hilang oleh foton akibat perluasan ruang di alam semesta (pergeseran merah kosmologis 1 + z = a -1 ).
Gambar berikut menunjukkan variasi materi dan kepadatan radiasi dengan waktu.
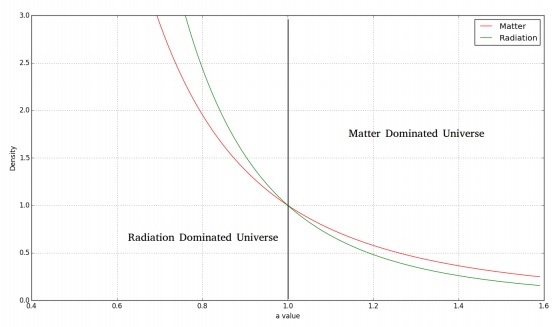
Untuk alam semesta yang datar dan didominasi radiasi, kita akan mendapatkan persamaan Friedmann sebagai berikut -
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G\rho}{3}$$
$$\left ( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3}\frac{\rho_0}{a^4}$$
Pada penyederhanaan dan penerapan solusi pada persamaan diferensial, kita memiliki -
$$(\dot{a})^2 = \frac{8\pi G\rho_0}{3a^2}$$
$$\Rightarrow a(t) \propto t^{\frac{1}{2}}$$
Jadi, kami memiliki -
$$a(t) = a_0 \left ( \frac{t}{t_0} \right )^{\frac{1}{2}}$$
Dari persamaan di atas, kita melihat bahwa laju peningkatan faktor skala lebih kecil daripada laju peningkatan faktor skala alam semesta berdebu.
Poin untuk Diingat
Radiasi yang lazim di alam semesta saat ini dapat dikaitkan sangat sedikit dengan sumber bintang.
Untuk alam semesta yang berdebu, tekanannya nol.
CMB sangat dingin.
Area Dark Energy adalah area yang sangat abu-abu dalam astronomi karena merupakan parameter bebas di semua persamaan, tetapi tidak ada gambaran jelas apa sebenarnya ini.
Kita akan mulai dengan persamaan Friedmann,
$$\left ( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2}$$
Sebagian besar buku dasar tentang kosmologi, semuanya dimulai dengan menggambarkan energi gelap dari episode ini bahwa sebelum pengamatan Hubble, alam semesta tertutup dan statis.
Sekarang, agar alam semesta menjadi statis di sisi kanan, kedua suku harus cocok dan harus nol, tetapi jika suku pertama lebih besar dari suku kedua, maka alam semesta tidak akan statis, jadi Einstein menjatuhkan parameter bebas ∧ ke dalam persamaan medan untuk membuat alam semesta statis, jadi dia berpendapat bahwa tidak peduli apa suku pertama dibandingkan dengan suku kedua, Anda selalu bisa mendapatkan alam semesta statis jika ada satu lagi komponen dalam persamaan, yang dapat mengkompensasi dis- kecocokan antara dua istilah ini.
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2} + \frac{\wedge}{3}$$
$$\left ( \frac{\ddot{a}}{a} \right ) = -\frac{4 \pi G}{3}\left ( \rho + \frac{3P}{c^2} \right ) + \frac{\wedge}{3}$$
Dimana $P = \rho \ast c^2/3$ dan $\wedge = \rho \ast c^2$adalah Parameter Kosmologis. (Tanda negatif hanya karena ketertarikan)
Dalam persamaan di atas (persamaan percepatan) -
$3P/c^2$ adalah tekanan negatif akibat radiasi,
$-4\pi G/3$ adalah tarikan karena gravitasi, dan
$\wedge/3$ memberikan kontribusi positif.
Suku ketiga bertindak sebagai gaya tolak karena bagian lain dari persamaan itu menarik.
Signifikansi fisik persamaan adalah itu ˙a = 0karena tidak ada bukti yang menunjukkan bahwa alam semesta mengembang. Bagaimana jika kedua istilah ini tidak cocok satu sama lain, jadi lebih baik menambahkan komponen dan tergantung pada offsetnya kita selalu dapat mengubah nilai parameter bebas.
Saat itu belum ada penjelasan fisik tentang parameter kosmologis ini, itulah sebabnya ketika penjelasan tentang alam semesta yang mengembang ditemukan pada tahun 1920-an, dimana Einstein segera harus membuang konstanta ini.
Penjelasan tentang ini cosmological constant masih digunakan karena menjelaskan versi yang berbeda dari alam semesta, tetapi definisi konstanta kosmologis ini, cara penafsirannya terus berubah seiring waktu.
Sekarang konsep konstanta kosmologis ini telah dibawa kembali ke kosmologi karena berbagai alasan. Salah satu alasannya adalah, kami memiliki pengamatan kepadatan energi berbagai komponen alam semesta (baryonic, dark matter, radiasi), jadi kami tahu apa parameter ini. Pengamatan independen menggunakancosmic microwave background menunjukkan bahwa k = 0.
$$CMB, k=0\: \rho = \rho_c = \frac{3H_0^2}{8\pi G} \approx 10 \: Hydrogen \: atoms.m^{-3}$$
Untuk k menjadi 0, $\rho$ harus sama dengan $\rho_c$, tetapi semua yang kita tahu jika kita menjumlahkannya tidak menghasilkan 0, yang berarti ada beberapa komponen lain yang menunjukkan bahwa nilainya jauh lebih kecil dari $\rho_c$.
$$\rho = \rho_b + \rho_{DM} + \rho_{rad} << \rho_c$$
Satu lagi bukti energi gelap berasal dari Type 1 Supernova Observationyang terjadi ketika katai putih menambah materi dan melebihi batas Chandrashekhar, yang merupakan batas yang sangat tepat (≈ 1.4M). Sekarang setiap kali terjadi Ledakan Supernova Tipe 1, kita memiliki massa yang sama yang berarti energi ikat total sistem sama dan jumlah energi cahaya yang dapat kita lihat juga sama.
Tentu saja, cahaya supernova meningkat dan kemudian pingsan, tetapi jika Anda mengukur kecerahan puncak, hasilnya akan selalu sama sehingga menjadi kandidat standar. Jadi, dengan Supernova Tipe 1 yang kami gunakan untuk mengukur komponen kosmologis alam semesta dan para astronom menemukan bahwa supernova dengan pergeseran merah tinggi 30% - 40% lebih redup daripada supernova pergeseran merah rendah dan dapat dijelaskan jika ada -nol∧ istilah.
Dalam model kosmologis DE (Dark Energy)diperlakukan sebagai fluida, yang berarti kita dapat menulis persamaan keadaan untuk itu. Persamaan keadaan adalah persamaan yang menghubungkan variabel seperti Tekanan, Massa jenis, Suhu, dan Volume dari dua keadaan materi yang berbeda.
Secara dimensi kita melihat,
$$\frac{8 \pi G}{3}\rho = \frac{\wedge}{3}$$
$$\rho_\wedge = \frac{\wedge}{8\pi G}$$
Kepadatan energi DE,
$$\epsilon_\wedge = \rho_\wedge \ast c^2 = \frac{\wedge c^2}{8 \pi G}$$
Parameter kepadatan energi gelap,
$$\Omega_\wedge = \frac{\rho_\wedge}{\rho_c}$$
$\Omega_\wedge$ adalah kepadatan energi gelap dalam hal massa jenis kritis.
$$\rho = \rho_b + \rho_{DM} +\rho_\wedge$$
Ada sejumlah teori tentang energi gelap, yang menolak alam semesta dan menyebabkan alam semesta mengembang. Salah satu hipotesisnya adalah bahwa energi gelap ini bisa jadi merupakan kepadatan energi vakum. Misalkan ruang itu sendiri sedang memproses sejumlah energi dan ketika Anda menghitung jumlah materi baryonik, materi gelap, dan radiasi dalam satuan volume ruang, Anda juga menghitung jumlah energi yang terkait dengan ruang, tetapi tidak jelas bahwa energi gelap sebenarnya adalah kepadatan energi vakum.
Kita tahu bahwa hubungan antara faktor kerapatan dan skala untuk materi gelap dan radiasi adalah,
$$\rho_m \propto \frac{1}{a^3}$$
$$\rho_m \propto \frac{1}{a^4}$$
Kami memiliki plot faktor skala kepadatan v / s. Di plot yang sama, kita bisa melihatnya$\rho_\wedge$ adalah konstanta dengan perluasan alam semesta yang tidak bergantung pada faktor skala.
Gambar berikut menunjukkan hubungan antara kepadatan dan faktor skala.

‘ρ’ v/s ‘a’(faktor skala yang terkait dengan waktu) dalam grafik yang sama, energi gelap dimodelkan sebagai konstanta. Jadi, energi gelap apa pun yang kita ukur di alam semesta saat ini, itu adalah konstanta.
Poin untuk Diingat
Pengamatan independen menggunakan latar belakang gelombang mikro kosmik menunjukkan bahwa k = 0.
$\rho_\wedge$ adalah konstanta dengan perluasan alam semesta yang tidak bergantung pada faktor skala.
Gravitasi juga berubah seiring dengan waktu yang disebut modified Newtonian dynamics.
Pada bab ini, kita akan membahas tentang Kurva Rotasi Galaksi Spiral dan bukti Materi Gelap.
Materi Gelap dan Fakta Pengamatan tentang Materi Gelap
Bukti Awal Materi Gelap adalah study of the Kinematics of Spiral Galaxy.
Matahari berjarak 30.000 tahun cahaya dari pusat galaksi kita. Kecepatan sentris galaksi adalah 220 km / s.
Mengapa kecepatan 220 km / s bukan 100 km / s atau 500 km / s? Apa yang mengatur gerak melingkar benda?
Massa yang tertutup dalam radius membantu mendeteksi kecepatan di alam semesta.
Rotasi Galaksi Bima Sakti atau Spiral - Rotasi Diferensial
Angular Velocity bervariasi dengan jarak dari pusat.
Jangka waktu orbit bergantung pada jarak dari pusat.
Materi yang lebih dekat dengan pusat galaksi memiliki jangka waktu yang lebih pendek dan materi yang jauh dari pusat galaksi memiliki jangka waktu yang lebih besar.
Kurva Rotasi
Memprediksi perubahan kecepatan dengan Galactic centric radius. Kurva yang memberikan kecepatan berubah dengan jari-jari orbit.
Ketika kita melihat sesuatu bergerak, kita mengira bahwa gravitasi yang mempengaruhi rotasi.
Distribusi massa bervariasi dengan jari-jari. Kepadatan materi akan memprediksi kurva rotasi. Kurva rotasi didasarkan pada kerapatan materi, yang bervariasi dengan jari-jari.
Kecerahan Permukaan
Kami memilih tambalan dan melihat berapa banyak cahaya yang keluar.
Jumlah cahaya yang berasal dari tambalan disebut sebagai Kecerahan Permukaan.
Satuannya adalah mag/arcsec2.
Jika kita menemukan kecerahan permukaan bervariasi dengan radius, kita dapat menemukan materi bercahaya bervariasi dengan radius.
$$\mu(r) \propto exp \left( \frac{-r}{h_R} \right )$$
$h_R$ adalah panjang skala. $\mu(r) = \mu_o \ast exp \left( \frac{-r}{h_R} \right )$
$h_R$ hampir 3 kpc untuk Bima Sakti.
Galaksi Spiral
Agar para astronom dapat memahami kurva rotasi, mereka membagi galaksi menjadi dua komponen, yaitu -
- Disk
- Bulge
Gambar berikut menunjukkan tonjolan bola pusat + Disk lingkaran. Distribusi bintang dan gas berbeda pada tonjolan dan cakram.

Kinematika Galaksi Spiral
-
Kecepatan melingkar benda apa pun - Untuk tonjolan adalah (r <Rb).
$$V^2(r) = G \ast \frac{M(r)}{r}$$
$$M(r) = \frac{4\pi r^3}{3} \ast \rho_b$$
-
Untuk disk - (Rb <r <Rd)
$$V^2(r) = G \ast \frac{M(r)}{r}$$
Bulge memiliki kepadatan bintang yang kira-kira konstan.
Kepadatan di dalam Bulge adalah konstan (tidak berubah dengan jarak di dalam tonjolan).
Dalam sebuah cakram, kerapatan bintang menurun seiring dengan jari-jari. Jari-jari bertambah kemudian materi bercahaya berkurang.
Dalam jumlah besar - $V(r) \propto r$
Dalam Disk - $V(r) \propto 1/\sqrt{r}$
Kurva Rotasi Galaksi Spiral
Melalui Spectroscopy (galaksi terdekat - galaksi spasial diselesaikan), kami menghasilkan kurva rotasi.
Seperti disebutkan di atas, kita melihat bahwa kurva rotasi datar di daerah terluar, yaitu benda-benda bergerak cepat di daerah terluar, yang umumnya tidak diharapkan dalam bentuk ini.
Kecepatan orbit meningkat dengan bertambahnya jari-jari daerah dalam, tetapi mendatar di daerah luar.
Materi Gelap
Materi Gelap dikatakan sebagai Komponen Alam Semesta yang Tidak Bercahaya. Mari kita pahami tentang materi gelap melalui petunjuk berikut.
Kurva rotasi datar berlawanan dengan apa yang kita lihat untuk distribusi bintang dan gas di galaksi spiral.
Luminositas permukaan piringan jatuh secara eksponensial dengan jari-jari, menyiratkan bahwa massa materi bercahaya, kebanyakan bintang, terkonsentrasi di sekitar pusat galaksi.
Perataan kurva rotasi menunjukkan bahwa massa total galaksi dalam radius tertentu r selalu meningkat dengan peningkatan r.
Ini hanya dapat dijelaskan jika ada sejumlah besar massa gravitasi tak terlihat di galaksi ini yang tidak memancarkan radiasi elektromagnetik.
Pengukuran kurva rotasi galaksi spiral adalah salah satu bukti paling meyakinkan untuk materi gelap.
Bukti Materi Gelap
Massa yang Hilang - 10 kali massa bercahaya.
Sebagian besar materi gelap ini pasti berada di lingkaran cahaya galaksi: Materi gelap dalam jumlah besar di cakram dapat mengganggu stabilitas jangka panjang cakram terhadap gaya pasang surut.
Beberapa bagian kecil dari materi gelap di cakram dapat berupa bintang baryonic - redup (katai coklat, katai hitam), dan sisa-sisa bintang kompak (bintang neutron, lubang hitam). Tapi materi gelap baryonic tidak dapat menjelaskan skala penuh dari massa yang hilang di galaksi.
Profil Kepadatan Materi Gelap - $M(r) \propto r$ dan $\rho(r) \propto r^{−2}$.
Data kurva rotasi untuk galaksi spiral konsisten dengan materi gelap yang terdistribusi dalam halo.
Halo gelap ini merupakan sebagian besar dari total massa galaksi.
Semua materi baryonic (bintang, gugus bintang, ISM, dll.) Disatukan oleh potensial gravitasi halo materi gelap ini.
Kesimpulan
Materi gelap hanya dapat dideteksi melalui interaksi gravitasinya dengan materi biasa. Belum ada interaksi dengan cahaya (tidak ada gaya elektromagnetik) yang diamati.
Neutrinos- Isi daya lebih sedikit, interaksi lemah, tetapi massa terlalu sedikit (<0,23 eV). Partikel DM harus memiliki E> 10 eV atau lebih untuk menjelaskan pembentukan struktur.
Weakly Interacting Massive Particles (WIMPS) dapat menjadi sumber Dark Matter.
Poin untuk Diingat
Materi yang lebih dekat ke pusat galaksi memiliki periode waktu yang lebih singkat.
Bulge memiliki kepadatan bintang yang kira-kira konstan.
Luminositas permukaan disk turun secara eksponensial dengan radius.
Materi gelap dalam jumlah besar dalam disk dapat mengganggu stabilitas jangka panjang disk terhadap gaya pasang surut.
Bukti langsung pertama dari materi gelap berasal Frids Ricky. Dia melakukan beberapa pengamatan yang mengungkapkan materi gelap untuk pertama kalinya. Pengamatannya mempertimbangkan gerakan keseluruhan dalam gugus galaksi.
Objek yang diperluas adalah gugus galaksi dan dianggap sebagai struktur terikat. Galaksi-galaksi ini bergerak sehubungan dengan pusat gugus tetapi tidak terbang. Kami melihat gerakan keseluruhan galaksi.
Asumsi: Kecepatan Mewakili Potensi yang Mendasari
Setiap galaksi akan memiliki gerak sendiri dalam gugus dan Hubble Flow Component. Galaksi yang lebih kecil lebih kecil, sebagian besar cahaya berasal dari M31 dan MW, ada beberapa galaksi katai. Untuk analisis kasar kami, kami hanya dapat menggunakan M31 dan MW dan mengevaluasi massa dinamis grup lokal.
Ada kecepatan relatif antara kita dan M31. Itu kasar, tapi itu benar. Ceritanya dimulai sejak lama ketika M31 dan MW dekat satu sama lain, karena mereka adalah anggota cluster, mereka saling menjauh. Setelah beberapa waktu mereka mencapai pemisahan maksimum, lalu semakin dekat satu sama lain.
Katakanlah pemisahan maksimum yang dapat dicapai adalah $r_{max}$. Sekarang mereka memiliki pemisahan yang disebutr. MembiarkanMmenjadi massa gabungan MW dan M31. Kami tidak tahu kapan$r_{max}$ tercapai.
$$\frac{GM}{r_{max}} = \:Potential \: at \:r_{max}$$
Ketika galaksi-galaksi ini mendekat satu sama lain pada suatu saat r, maka energi sistem akan menjadi -
$$\frac{1}{2}\sigma^2 = \frac{GM}{r} = \frac{GM}{r_{max}}$$
σ adalah kecepatan relatif kedua galaksi. M adalah massa tereduksi saja, tetapi massa uji adalah 1. σ adalah kecepatan benda apa pun pada jarak rdari tengah cluster. Kami percaya bahwa cluster ini berada dalam persamaan dinamis karena teori virial berlaku. Jadi, galaksi tidak bisa datang dengan kecepatan berbeda.
Berapa lama waktu yang dibutuhkan galaksi-galaksi ini untuk mencapai jarak maksimum?
Untuk memahami ini, mari kita perhatikan persamaan berikut.
$$\frac{1}{2}\left ( \frac{dr}{dt} \right )^2 = \frac{GM}{r} - \frac{GM}{r_{max}}$$
$$t_{max} = \int_{0}^{r_{max}} dt = \int_{0}^{r_{max}} \frac{dr}{\sqrt{2GM}}\left ( \frac{1}{r} - \frac{1}{r_{max}} \right )^2$$
$$t_{max} = \frac{\pi r_{max}^{\frac{3}{2}}}{2\sqrt{2GM}}$$
Dimana, M = massa dinamis kelompok lokal. Total waktu dari awal hingga akhir tumbukan adalah$2t_{max}$. Karena itu,
$$2t_{max} = t_0 + \frac{D}{\sigma}$$
Dan $t_0$ adalah zaman alam semesta saat ini.
Jika sebenarnya $t_{max} < RHS$, maka kami memiliki batas waktu yang lebih rendah. $D/\sigma$adalah saat dimana mereka akan bertabrakan lagi. Di sini, kami mengasumsikan σ konstan.
$$t_{max} = \frac{t_0}{2} + \frac{D}{2\sigma}$$
$$r_{max} = t_{max} \times \sigma = 770K_{pc}$$
Di sini, σ = kecepatan relatif antara MW dan M31.
$$M_{dynamic} = 3 \times 10^{12}M_0$$
$$M_{MW}^{lum} = 3 \times 10^{10}M_0$$
$$M_{M31}^{lum} = 3 \times 10^{10}M_0$$
Tapi secara praktis, massa dinamis ditemukan dengan mempertimbangkan setiap galaksi di dalam gugusnya. Massa yang hilang adalah materi gelap danFrids Rickyperhatikan bahwa galaksi dalam gugus koma bergerak terlalu cepat. Dia meramalkan keberadaan bintang neutron setahun setelah bintang neutron ditemukan dan menggunakan teleskop Palomar untuk menemukan supernova.
Poin untuk Diingat
Bukti langsung pertama dari materi gelap berasal Frids Ricky.
Objek yang diperluas adalah gugus galaksi dan dianggap bound structures.
Dynamic mass ditemukan dengan mempertimbangkan setiap galaksi di dalam cluster.
Pada bab ini, kita akan membahas tentang parameter Density dan Hubble.
Parameter Hubble
Parameter Hubble didefinisikan sebagai berikut -
$$H(t) \equiv \frac{da/dt}{a}$$
yang mengukur seberapa cepat faktor skala berubah. Secara umum, evolusi faktor skala ditentukan oleh Persamaan Friedmann.
$$H^2(t) \equiv \left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho - \frac{kc^2}{a^2} + \frac{\wedge}{3}$$
dimana, ∧ adalah konstanta kosmologis.
Untuk alam semesta datar, k = 0, maka Persamaan Friedmann menjadi -
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho + \frac{\wedge}{3}$$
Untuk materi yang mendominasi alam semesta, kepadatannya bervariasi sebagai -
$$\frac{\rho_m}{\rho_{m,0}} = \left ( \frac{a_0}{a} \right )^3 \Rightarrow \rho_m = \rho_{m,0}a^{-3}$$
dan, untuk alam semesta yang didominasi radiasi, kepadatannya bervariasi sebagai -
$$\frac{\rho_{rad}}{\rho_{rad,0}} = \left ( \frac{a_0}{a} \right )^4 \Rightarrow \rho_{rad} = \rho_{rad,0}a^{-4}$$
Saat ini, kita hidup di alam semesta yang didominasi materi. Oleh karena itu, pertimbangkan$\rho ≡ \rho_m$, kami mendapatkan -
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho_{m,0}a^{-3} + \frac{\wedge}{3}$$
Konstanta kosmologis dan kepadatan energi gelap terkait sebagai berikut -
$$\rho_\wedge = \frac{\wedge}{8 \pi G} \Rightarrow \wedge = 8\pi G\rho_\wedge$$
Dari sini, kami mendapatkan -
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho_{m,0}a^{-3} + \frac{8 \pi G}{3} \rho_\wedge$$
Juga, kerapatan kritis dan konstanta Hubble terkait sebagai berikut -
$$\rho_{c,0} = \frac{3H_0^2}{8 \pi G} \Rightarrow \frac{8\pi G}{3} = \frac{H_0^2}{\rho_{c,0}}$$
Dari sini, kami mendapatkan -
$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{H_0^2}{\rho_{c,0}}\rho_{m,0}a^{-3} + \frac{H_0^2}{\rho_{c,0}}\rho_\wedge$$
$$\left ( \frac{\dot{a}}{a} \right )^2 = H_0^2\Omega_{m,0}a^{-3} + H_0^2\Omega_{\wedge,0}$$
$$(\dot{a})^2 = H_0^2\Omega_{m,0}a^{-1} + H_0^2\Omega_{\wedge,0}a^2$$
$$\left ( \frac{\dot{a}}{H_0} \right )^2 = \Omega_{m,0}\frac{1}{a} + \Omega_{\wedge,0}a^2$$
$$\left ( \frac{\dot{a}}{H_0} \right )^2 = \Omega_{m,0}(1+z) + \Omega_{\wedge,0}\frac{1}{(1+z)^2}$$
$$\left ( \frac{\dot{a}}{H_0} \right)^2 (1+z)^2 = \Omega_{m,0}(1+z)^3 + \Omega_{\wedge,0}$$
$$\left ( \frac{\dot{a}}{H_0} \right)^2 \frac{1}{a^2} = \Omega_{m,0}(1 + z)^3 + \Omega_{\wedge,0}$$
$$\left ( \frac{H(z)}{H_0} \right )^2 = \Omega_{m,0}(1+z)^3 + \Omega_{\wedge,0}$$
Sini, $H(z)$adalah parameter Hubble yang bergantung pada pergeseran merah. Ini dapat dimodifikasi untuk memasukkan parameter kepadatan radiasi$\Omega_{rad}$ dan parameter kepadatan kelengkungan $\Omega_k$. Persamaan yang dimodifikasi adalah -
$$\left ( \frac{H(z)}{H_0} \right )^2 = \Omega_{m,0}(1+z)^3 + \Omega_{rad,0}(1+z)^4+\Omega_{k,0}(1+z)^2+\Omega_{\wedge,0}$$
$$Or, \: \left ( \frac{H(z)}{H_0} \right)^2 = E(z)$$
$$Or, \: H(z) = H_0E(z)^{\frac{1}{2}}$$
dimana,
$$E(z) \equiv \Omega_{m,0}(1 + z)^3 + \Omega_{rad,0}(1+z)^4 + \Omega_{k,0}(1+z)^2+\Omega_{\wedge,0}$$
Ini menunjukkan bahwa parameter Hubble bervariasi dengan waktu.
Untuk Einstein-de Sitter Alam semesta, $\Omega_m = 1, \Omega_\wedge = 0, k = 0$.
Dengan memasukkan nilai-nilai ini, kami mendapatkan -
$$H(z) = H_0(1+z)^{\frac{3}{2}}$$
yang menunjukkan evolusi waktu parameter Hubble untuk alam semesta Einstein-de Sitter.
Parameter Kepadatan
Parameter kepadatan, $\Omega$, didefinisikan sebagai rasio kepadatan aktual (atau yang diamati) ρ dengan kepadatan kritis $\rho_c$. Untuk kuantitas berapa pun$x$ parameter kepadatan yang sesuai, $\Omega_x$ dapat dinyatakan secara matematis sebagai -
$$\Omega_x = \frac{\rho_x}{\rho_c}$$
Untuk jumlah berbeda yang dipertimbangkan, kita dapat menentukan parameter kepadatan berikut.
| S.No. | Kuantitas | Parameter Kepadatan |
|---|---|---|
| 1 | Baryons | $\Omega_b = \frac{\rho_b}{\rho_c}$ |
| 2 | Materi (Baryonic + Dark) | $\Omega_m = \frac{\rho_m}{\rho_c}$ |
| 3 | Energi Gelap | $\Omega_\wedge = \frac{\rho_\wedge}{\rho_c}$ |
| 4 | Radiasi | $\Omega_{rad} = \frac{\rho_{rad}}{\rho_c}$ |
Dimana simbol memiliki arti yang biasa.
Poin untuk Diingat
Evolusi faktor skala ditentukan oleh Friedmann Equation.
H(z) adalah parameter Hubble yang bergantung pada pergeseran merah.
Itu Hubble Parameter bervariasi dengan waktu.
Itu Density Parameter didefinisikan sebagai rasio kepadatan aktual (atau yang diamati) dengan kepadatan kritis.
Seperti yang dibahas di bab sebelumnya, evolusi waktu parameter Hubble diberikan oleh -
$$H(z) = H_0E(z)^{\frac{1}{2}}$$
Dimana z adalah pergeseran merah dan E(Z) adalah -
$$E(z) \equiv \Omega_{m,0}(1+z)^3 + \Omega(1+z)^4 +\Omega_{k,0}(1+z)^2 + \Omega^{\wedge,0}$$
Jika perluasan alam semesta konstan, maka umur sebenarnya dari alam semesta diberikan sebagai berikut -
$$t_H = \frac{1}{H_0}$$
Jika materi yang mendominasi alam semesta, yaitu alam semesta Einstein Desitter, maka usia sebenarnya dari alam semesta diberikan oleh -
$$t_H = \frac{2}{3H_0}$$
Skala dan Redshift ditentukan oleh -
$$a=\frac{a_0}{1+z}$$
Umur alam semesta dalam parameter kosmologis diturunkan sebagai berikut.
Parameter Hubble diberikan oleh -
$$H = \frac{\frac{da}{dt}}{a}$$
Membedakan, kita dapatkan -
$$da = \frac{-dz}{(1+z)^2}$$
Dimana a0 = 1 (nilai sekarang dari faktor skala)
$$\frac{\mathrm{d} a}{\mathrm{d} t} = \frac{-1}{(1+z)^2}$$
$$\frac{\mathrm{d} a}{\mathrm{d} t} = \frac{\mathrm{d} a}{\mathrm{d} t}\frac{\mathrm{d} z}{\mathrm{d} t}$$
$$H = \frac{\dot{a}}{a} = \frac{\mathrm{d} a}{\mathrm{d} t}\frac{\mathrm{d} z}{\mathrm{d} t} \frac{1+z}{1}$$
$$\frac{\dot{a}}{a} = \frac{-1}{1+z}\frac{\mathrm{d} z}{\mathrm{d} t}\frac{1}{1}$$
$$H(z) = H_0E(z)^{\frac{1}{2}}$$
$$dt = \frac{-dz}{H_0E(z)^{\frac{1}{2}}(1+z)}$$
Jika kita ingin menemukan usia alam semesta pada pergeseran merah tertentu ‘z’ kemudian -
$$t(z) = \frac{1}{H_0}\int_{\infty}^{z_1} \frac{-1}{E(z)^{\frac{1}{2}}(1+z)}dz$$
Dimana k adalah parameter kepadatan kelengkungan dan -
$$E(z) \equiv \Omega_{m,0}(1+z)^3 + \Omega_{rad,0}(1+z)^4 + \Omega_{k,0}(1+z)^2 + \Omega_{\wedge,0}$$
Untuk menghitung usia alam semesta saat ini, ambillah z1 = 0.
$$t(z=0) = t_{age} = t_0 = \frac{1}{H_0}\int_{\infty}^{z_1} \frac{-1}{E(z)^{\frac{1}{2}}(1+z)}dz$$
Untuk Model Einstein Desitter, yaitu, $\Omega_m = 1$, $\Omega_{rad} = 0$, $\Omega_k = 0$, $\Omega_\wedge = 0$, persamaan usia alam semesta menjadi -
$$t_{age} = \frac{1}{H_0}\int_{0}^{\infty} \frac{1}{(1+z)^{\frac{5}{2}}}dz$$
Setelah menyelesaikan integral, kita mendapatkan -
$$t_H = \frac{2}{3H_0}$$
Langit malam seperti a Cosmic Time Machine.Setiap kali kita mengamati planet, bintang, atau galaksi yang jauh, kita melihatnya seperti berjam-jam, berabad-abad, atau bahkan ribuan tahun yang lalu. Ini karena cahaya bergerak pada kecepatan yang terbatas (kecepatan cahaya) dan mengingat jarak yang jauh di Semesta, kita tidak melihat objek seperti sekarang, tetapi seperti saat cahaya dipancarkan. Waktu yang telah berlalu antara - saat kita mendeteksi cahaya di Bumi dan saat awalnya dipancarkan oleh sumbernya, dikenal sebagaiLookback Time (tL(z1)).
Jadi, waktu lihat balik diberikan oleh -
$$t_1(z_1) = t_0-t(z_1)$$
Waktu melihat ke belakang untuk Einstein Desitter Universe adalah -
$$t_L(z) = \frac{2}{3H_0}\left [ 1- \frac{1}{(1+z)^{\frac{3}{2}}} \right ]$$
Poin untuk Diingat
Setiap kali kita mengamati planet, bintang, atau galaksi yang jauh, kita melihatnya seperti berjam-jam, berabad-abad, atau bahkan ribuan tahun yang lalu.
Waktu yang berlalu antara - saat kita mendeteksi cahaya di Bumi dan saat awalnya dipancarkan oleh sumbernya, dikenal sebagai waktu lookback.
Dalam bab ini, kita akan memahami apa itu Jarak Diameter Sudut dan bagaimana hal itu membantu dalam Kosmologi.
Untuk alam semesta saat ini -
$\Omega_{m,0} \: = \: 0.3$
$\Omega_{\wedge,0} \: = \: 0.69$
$\Omega_{rad,0} \: = \: 0.01$
$\Omega_{k,0} \: = \: 0$
Kami telah mempelajari dua jenis jarak sampai sekarang -
Proper distance (lp) - Jarak yang ditempuh foton dari sumber ke kita, yaitu The Instantaneous distance.
Comoving distance (lc) - Jarak antar objek dalam ruang yang tidak meluas, yaitu, distance in a comoving frame of reference.
Jarak sebagai Fungsi Pergeseran Merah
Pertimbangkan galaksi yang memancarkan foton pada suatu waktu t1 yang terdeteksi oleh pengamat di t0. Kita dapat menulis jarak yang tepat ke galaksi sebagai -
$$l_p = \int_{t_1}^{t_0} cdt$$
Biarkan pergeseran merah galaksi terjadi z,
$$\Rightarrow \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{1}{a^2}\frac{\mathrm{d} a}{\mathrm{d} t}$$
$$\Rightarrow \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{\frac{\mathrm{d} a}{\mathrm{d} t}}{a}\frac{1}{a}$$
$$\therefore \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{H(z)}{a}$$
Sekarang, galaksi bergerak jarak kapan saja t akan -
$$l_c = \frac{l_p}{a(t)}$$
$$l_c = \int_{t_1}^{t_0} \frac{cdt}{a(t)}$$
Dari segi z,
$$l_c = \int_{t_0}^{t_1} \frac{cdz}{H(z)}$$
Ada dua cara untuk mencari jarak, yaitu sebagai berikut -
Hubungan Fluks-Luminositas
$$F = \frac{L}{4\pi d^2}$$
dimana d adalah jarak di sumbernya.
Jarak Diameter Sudut Sumber
Jika kita mengetahui ukuran sumber, lebar sudutnya akan memberi tahu kita jaraknya dari pengamat.
$$\theta = \frac{D}{l}$$
dimana l adalah jarak diameter sudut dari sumber.
θ adalah ukuran sudut sumber.
D adalah ukuran sumbernya.
Pertimbangkan galaksi berukuran D dan ukuran sudut dθ.
Kami tahu itu,
$$d\theta = \frac{D}{d_A}$$
$$\therefore D^2 = a(t)^2(r^2 d\theta^2) \quad \because dr^2 = 0; \: d\phi ^2 \approx 0$$
$$\Rightarrow D = a(t)rd\theta$$
Berubah r untuk rc, jarak galaksi yang sedang bergerak, kita memiliki -
$$d\theta = \frac{D}{r_ca(t)}$$
Di sini, jika kita memilih t = t0, kami akhirnya mengukur jarak saat ini ke galaksi. TapiDdiukur pada saat emisi foton. Oleh karena itu, dengan menggunakant = t0, kita mendapatkan jarak yang lebih jauh ke galaksi dan karenanya meremehkan ukurannya. Oleh karena itu, kita harus memanfaatkan waktut1.
$$\therefore d\theta = \frac{D}{r_ca(t_1)}$$
Membandingkan ini dengan hasil sebelumnya, kita mendapatkan -
$$d_\wedge = a(t_1)r_c$$
$$r_c = l_c = \frac{d_\wedge}{a(t_1)} = d_\wedge(1+z_1) \quad \because 1+z_1 = \frac{1}{a(t_1)}$$
Karena itu,
$$d_\wedge = \frac{c}{1+z_1} \int_{0}^{z_1} \frac{dz}{H(z)}$$
dA adalah Jarak Diameter Sudut untuk objek.
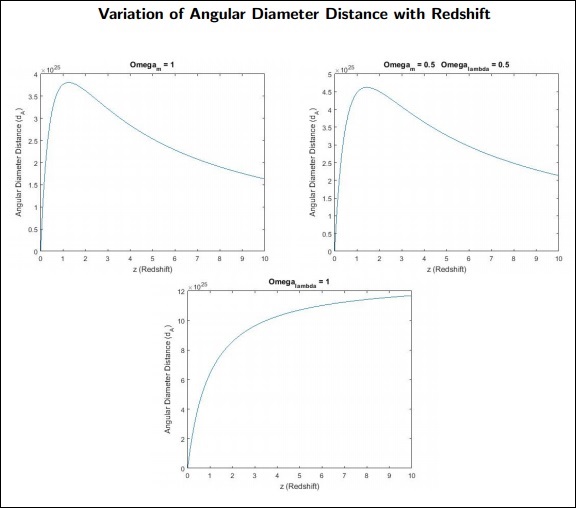
Poin untuk Diingat
Jika kita mengetahui ukuran sumber, lebar sudutnya akan memberi tahu kita jaraknya dari pengamat.
Jarak yang tepat adalah jarak yang ditempuh foton dari sumber ke kita.
Comoving distance adalah jarak antar objek dalam suatu ruang yang tidak meluas.
Seperti dibahas pada bab sebelumnya, jarak diameter sudut ke sumber pada pergeseran merah z diberikan oleh -
$$d_\wedge (z_{gal}) = \frac{c}{1+z_{gal}}\int_{0}^{z_{gal}} \frac{1}{H(z)}dz$$
$$d_\wedge(z_{gal}) = \frac{r_c}{1+z_{gal}}$$
dimana $r_c$ adalah jarak tempuh.
Jarak Luminositas bergantung pada kosmologi dan didefinisikan sebagai jarak di mana fluks yang diamati f berasal dari suatu objek.
Jika luminositas intrinsik $d_L$ dari suatu benda yang jauh diketahui, kita dapat menghitung luminositasnya dengan mengukur fluksnya $f$ yang ditentukan oleh -
$$d_L(z) = \sqrt{\frac{L}{4\pi f}}$$
Energi Foton berubah menjadi merah.
$$\frac{\lambda_{obs}}{\lambda_{emi}} = \frac{a_0}{a_e}$$
dimana $\lambda_{obs}, \lambda_{emi}$ diamati dan dipancarkan panjang gelombang dan $a_0, a_e$ adalah faktor skala yang sesuai.
$$\frac{\Delta t_{obs}}{\Delta t_{emi}} = \frac{a_0}{a_e}$$
dimana $\Delta_t{obs}$ diamati sebagai interval waktu foton, sedangkan $\Delta_t{emi}$ adalah interval waktu di mana mereka dipancarkan.
$$L_{emi} = \frac{nhv_{emi}}{\Delta t_{emi}}$$
$$L_{obs} = \frac{nhv_{obs}}{\Delta t_{obs}}$$
$\Delta t_{obs}$ akan membutuhkan lebih banyak waktu daripada $\Delta t_{emi}$ karena detektor harus menerima semua foton.
$$L_{obs} = L_{emi}\left ( \frac{a_0}{a_e} \right )^2$$
$$L_{obs} < L_{emi}$$
$$f_{obs} = \frac{L_{obs}}{4\pi d_L^2}$$
Untuk alam semesta yang tidak mengembang, jarak luminositas sama dengan jarak comoving.
$$d_L = r_c$$
$$\Rightarrow f_{obs} = \frac{L_{obs}}{4\pi r_c^2}$$
$$f_{obs} = \frac{L_{emi}}{4 \pi r_c^2}\left ( \frac{a_e}{a_0} \right )^2$$
$$\Rightarrow d_L = r_c\left ( \frac{a_0}{a_e} \right )$$
Kami menemukan jarak luminositas $d_L$ untuk menghitung luminositas objek yang memancarkan $L_{emi}$ -
Interpretation - Jika kita tahu pergeseran merahnya z galaksi manapun, kita bisa mencari tahu $d_A$ dan dari situ kita bisa menghitung $r_c$. Ini digunakan untuk mencari tahu$d_L$.
Jika $d_L ! = r_c(a_0/a_e)$, maka kami tidak dapat menemukan Lemi $f_{obs}$.
Hubungan antara Jarak Luminositas $d_L$ dan Jarak Diameter Sudut $d_A.$
Kami tahu bahwa -
$$d_A(z_{gal}) = \frac{d_L}{1+z_{gal}}\left ( \frac{a_0}{a_e} \right )$$
$$d_L = (1 + z_{gal})d_A(z_{gal})\left ( \frac{a_0}{a_e} \right )$$
Faktor skala ketika foton dipancarkan diberikan oleh -
$$a_e = \frac{1}{(1+z_{gal})}$$
Faktor skala alam semesta saat ini adalah -
$$a_0 = 1$$
$$d_L = (1 + z_{gal})^2d_\wedge(z_{gal})$$
Yang mana yang harus dipilih $d_L$ atau $d_A$?
Untuk galaksi dengan ukuran yang diketahui dan pergeseran merah untuk menghitung besarnya, maka $d_A$ digunakan.
Jika ada galaksi dengan magnitudo tampak tertentu, maka untuk mengetahui besarnya, $d_L$ digunakan.
Example - Jika diketahui bahwa dua galaksi dengan pergeseran merah yang sama (z = 1) dan pada bidang langit dipisahkan oleh 2.3 arc sec lalu berapa jarak fisik maksimum antara keduanya?
Untuk ini, gunakan $d_A$ sebagai berikut -
$$d_A(z_{gal}) = \frac{c}{1+z_{gal}}\int_{0}^{z_{gal}} \frac{1}{H(z)}dz$$
dimana z = 1 menggantikan H (z) berdasarkan parameter kosmologis galaksi.
Poin untuk Diingat
Jarak luminositas tergantung cosmology.
Jika luminositas intrinsik $d_L$ dari suatu benda yang jauh diketahui, kita dapat menghitung luminositasnya dengan mengukur fluksnya f.
Untuk alam semesta yang tidak mengembang, jarak luminositas sama dengan comoving distance.
Jarak luminositas selalu lebih besar dari Angular Diameter Distance.
Untuk setiap pergeseran merah (z), kita memiliki dua nilai untuk jarak -
- Jarak Diameter Sudut (d A )
- Jarak Luminositas (d L )
Tidak ada definisi unik tentang jarak "kosmologis" di alam semesta. Pilihan jarak tergantung pada tujuan dan kenyamanan aplikasi.
Untuk menguji tren prediksi bagaimana ukuran sudut suatu objek bervariasi dengan pergeseran merah, diperlukan tolok ukur ukuran standar di langit. Ini harus menjadi objek yang -
sangat bercahaya, sehingga dapat dideteksi pada z> 1.
sangat besar, sehingga kami dapat menentukan ukuran sudutnya.
belum berkembang secara morfologis selama waktu yang signifikan secara kosmologis (z ∼ 1 sesuai dengan waktu melihat ke belakang sekitar 7 Gyr).
Beberapa objek (seperti galaksi cD) memenuhi dua kriteria pertama. Tetapi hampir setiap objek ditemukan berevolusi secara morfologis seiring waktu. Secara umum, objek astrofisika (sumber diperpanjang) cenderung secara intrinsik lebih kecil di masa lalu karena masih dalam bentuk.
Jarak Luminositas
Jarak luminositas bergantung pada kosmologi. Ketergantungan jarak luminositas pada kosmologi membuatnya menjadi ukuran parameter kosmologis yang berguna.
Parameter kosmologis dapat diperkirakan jika kita dapat menemukan candle standar yang tidak berevolusi secara intrinsik dan ada dari lokal hingga jagat raya pergeseran merah tinggi.
Lilin standar adalah lilin yang tidak berbeda luminositasnya dari sumber ke sumber. Premisnya adalah bahwa perbedaan apa pun dalam perkiraan luminositas lilin standar harus disebabkan oleh kosmologi. Salah satu lilin tersebut adalah Supernova Tipe Ia.
Tipe 1a Supernova (SNe)
Ini adalah hasil ledakan katai putih setelah pertambahan massa yang cukup dari rekannya, raksasa merah atau bintang deret utama serupa, dalam sistem biner. Setelah raksasa merah datang lebih dekat dari jarak lobus Roche dari katai putih, perpindahan massa dimulai dan akhirnya katai putih itu meledak memberikan energi dalam jumlah besar, tanpa meninggalkan inti. Ini disebut Tipe 1a Supernova. Tingkat tipikal ledakan Supernova Tipe 1a di galaksi adalah 1 per abad.
Pencarian untuk Tipe 1a SNe telah berlangsung dengan tim yang berbeda -
- Tim Pencarian Supernova z Tinggi (Brian Schmidt, Adam Reiss dkk.)
- Proyek Kosmologi Supernova (Saul Perlmutter et al.)
Ada tim peneliti lain yang dipanggil Carnegie Supernovae Project yang telah memberikan hasil serupa.
Kesamaan hasil dari tim yang berbeda menunjukkan sifat kosmologis SNe Tipe 1a. Karenanya, ini adalah candle standar yang efisien.
Poin untuk Diingat
Tidak ada definisi unik tentang jarak "kosmologis" di alam semesta.
Jarak Diameter Sudut dan Jarak Luminositas adalah yang paling banyak digunakan.
Lilin standar adalah lilin yang tidak berbeda luminositasnya dari sumber ke sumber.
Tipe 1a SNe memenuhi kriteria sebagai candle standar.
CMB (Latar Belakang Gelombang Mikro Kosmik) pada dasarnya dibentuk oleh foton saat materi dan radiasi berada dalam kesetimbangan. Pada 1920-an, gagasan tentang alam semesta yang mengembang diterima dan dapat menjawab beberapa pertanyaan. Tetapi pertanyaan tentang kelimpahan unsur-unsur yang lebih berat dan kelimpahan tidak terjawab. Selain itu, alam semesta yang mengembang menyiratkan bahwa kepadatan materi harus berkurang hingga 0.
Pada tahun 1948, George Gammow dan Ralph Alpher menjelaskan asal mula unsur-unsur yang lebih berat dan kelimpahannya menggunakan “Big Bang”. Mereka bersama Robert Herman meramalkan adanya “Relict Radiation” atau radiasi sisa dari “Big Bang”. Suhu yang diprediksi untuk sisa radiasi ini adalah antara 50-6 K. Pada tahun 1965, Robert Dicke, Jim Peebles dan David Wilkinson bersama dengan Kelompok Riset Amo Perizias secara eksperimental mendeteksi CMB.
Alam semesta awal sangat panas dan energinya terlalu tinggi untuk materi tetap netral. Oleh karena itu, materi berada dalam bentuk terionisasi -Plasma. Radiasi (foton) dan Materi (plasma) berinteraksi terutama melalui tiga proses berikut.
Compton Scattering - (Proses Interaksi Utama) Hamburan tidak elastis antara foton berenergi tinggi dan partikel bermuatan energi rendah.
Thomson Scattering - Hamburan foton elastis oleh partikel bermuatan bebas.
Inverse Compton Scattering- Partikel bermuatan energi tinggi dan foton energi rendah. Interaksi ini akhirnya menghasilkan materi dan radiasi dalam kesetimbangan termal.
Ekuilibrium Termal
Dalam kesetimbangan termal, radiasi mematuhi Planck Distribution of Energy,
$$B_v(T) = \frac{2hv^3}{c(e^{hv/k_BT}-1)}$$
Selama waktu ini, karena interaksi yang sangat sering, jalur bebas foton rata-rata sangat kecil. Alam semesta buram terhadap radiasi. Alam semesta awal didominasi radiasi. Alam semesta berevolusi sedemikian rupa sehingga materi dan radiasi mencapai kesetimbangan termal dan kepadatan energinya menjadi sama. Hal ini terlihat dari grafik yang menunjukkan evolusi massa jenis dengan faktor skala. Mari kita cari tahu faktor skala (waktu) (a (t)) di mana materi dan radiasi mencapai kesetimbangan.
$$\rho_m \propto \frac{1}{a^3}, \: \rho_r \propto \frac{1}{a^4}$$
$$\frac{\rho_{m,t}}{\rho_{r,t}} = \frac{\Omega_{m,t}}{\Omega_{r,t}} = \frac{\Omega_{m,0}}{\Omega_{r,0}}a(t)$$
Pada kesetimbangan,
$$\frac{\rho_{m,t}}{\rho_{r,t}} = \frac{\Omega_{m,t}}{\Omega_{r,t}} = 1$$
$$\Rightarrow \frac{\Omega_{m,0}}{\Omega_{r,0}}a(t) = 1 \: \Rightarrow a(t) = 2.96 \times 10^{-4}$$
menggunakan $\Omega_{m,0} = 0.27$ dan $\Omega_{r,0} = 8 \times 10^{−5}$. Pergeseran merah yang sesuai dengan faktor skala ini diberikan oleh -
$$z = 1/a(t)-1 \approx 3375$$
Kepadatan energi radiasi turun karena perluasan alam semesta. Jadi alam semesta mulai mendingin. Ketika energi foton mulai berkurang, atom netral mulai terbentuk. Dengan demikian, sekitar pergeseran merah 1300, Hidrogen netral mulai terbentuk. Era ini memiliki suhu mendekati 3000K.
Interaksi antara materi dan radiasi menjadi sangat jarang dan dengan demikian alam semesta mulai menjadi transparan terhadap radiasi. Jangka waktu ini disebut“Surface of last scattering”karena jalur bebas rata-rata foton menjadi sangat besar sehingga hampir tidak ada hamburan yang terjadi setelah periode ini. Itu juga disebut sebagai“Cosmic Photosphere”.
Poin untuk Diingat
CMB dibentuk oleh foton saat materi dan radiasi berada dalam kesetimbangan.
Alam semesta awal sangat panas dan energinya terlalu tinggi untuk materi tetap netral, jadi ia ada sebagai materi-Plasma terionisasi.
Compton Hamburan, Hamburan Thomson, Hamburan Compton Terbalik adalah proses interaksi radiasi 3 materi kemudian.
Alam semesta berevolusi sedemikian rupa sehingga materi dan radiasi mencapai kesetimbangan termal.
Pertama-tama kita harus memahami apa yang menjadi ciri decoupling. Kita tahu bahwa energi jauh lebih tinggi sedemikian rupa sehingga materi hanya ada dalam bentukIonized Particles. Jadi, pada masa pelepasan gandengan dan rekombinasi, energi harus turun untuk memungkinkan ionisasi hidrogen. Perhitungan perkiraan dapat dilakukan untuk perkiraan suhu pada saat decoupling.
Ini telah dilakukan sebagai berikut -
Pertama, pertimbangkan hanya ionisasi hidrogen keadaan dasar.
$$hv \approx k_BT$$
$$\therefore T \approx \frac{hv}{k_B}$$
Untuk ionisasi hidrogen keadaan dasar, hν adalah 13,6 eV dan kB adalah Boltzmann Constant8,61 × 10 −5 eV / K yang menunjukkan suhu 1,5 × 105 kelvin.
Ini pada dasarnya memberi tahu kita bahwa jika suhu di bawah 1,5 × 10 5 K, atom netral dapat mulai terbentuk.
Kita tahu bahwa rasio foton terhadap baryon adalah sekitar 5 × 10 10 . Oleh karena itu, bahkan pada bagian ekor grafik di mana jumlah foton berkurang, masih terdapat cukup foton untuk mengionisasi atom hidrogen. Selain itu, rekombinasi elektron dan proton tidak menjamin atom hidrogen dalam keadaan dasar. Keadaan terangsang membutuhkan energi yang lebih rendah untuk ionisasi. Oleh karena itu, analisis statistik yang disiplin harus dilakukan kasus per kasus untuk mendapatkan nilai yang akurat. Perhitungan mengatur suhu menjadi sekitar 3000K.
Demi penjelasan, kami mempertimbangkan kasus hidrogen yang menarik ke dalam keadaan tereksitasi pertama. Persamaan umum untuk rasio jumlah foton dengan energi lebih dariΔE, Nγ (> ΔE) dengan jumlah total foton Nγ diberikan oleh -
$$\frac{N_\gamma(> \Delta E)}{N_\gamma} \propto e^{\frac{-\Delta E}{kT}}$$
Untuk kasus menarik hidrogen ke keadaan tereksitasi pertama, ΔEadalah 10,2 eV. Sekarang, jika kita mempertimbangkan bilangan yang sangat konservatif minimal 1 foton dengan energi lebih dari 10,2 untuk setiap baryon (ingat bahwa rasionya adalah 5 × 10 10 , kita memperoleh suhu dari persamaan 3 sebagai 4800 K (Nγ yang disisipkan (> ΔE) = Np).
Ini adalah suhu untuk membuat populasi atom hidrogen netral dalam keadaan tereksitasi pertama. Suhu untuk mengionisasi ini jauh lebih rendah. Dengan demikian, kami memperoleh perkiraan yang lebih baik dari 1,5 × 10 5 K yang lebih dekat dengan nilai yang diterima 3000 K.
Redshift - Hubungan Suhu
Untuk memahami hubungan antara pergeseran merah dan suhu, kami menggunakan dua metode berikut seperti yang dijelaskan di bawah ini.
Metode 1
Dari Wien’s Law, kami tahu itu
$$\lambda_mT = constant$$
Untuk menghubungkan ini dengan pergeseran merah, kami menggunakan -
$$1+z = \frac{\lambda_0}{\lambda_e}$$
Sebagai $λ_oT_o = λ_eT(z)$, kami mendapatkan -
$$T(z) = T_0\frac{\lambda_0}{\lambda_e} = T_0(1+z)$$
Pengaturan To sebagai nilai saat ini 3K, kita bisa mendapatkan nilai suhu untuk pergeseran merah tertentu.
Metode 2
Dalam hal frekuensi, kita tahu -
$$v_0 = \frac{v_e}{1+z}$$
$$B_vdv = \frac{2hv^3}{c^2} \frac{dv}{e^{hv/kT}-1}$$
Ini memberitahu kita tentang energi bersih foton untuk interval energi dan hνadalah energi foton tunggal. Oleh karena itu, kita dapat memperoleh jumlah foton denganBνdν/hν.
Jika $n_{νo}$ adalah untuk saat ini dan $n_{νe}$ untuk dipancarkan, kami mendapatkan -
$$\frac{n_{v_e}}{n_{v_0}} = (1+z)^3$$
Pada penyederhanaan, kami mendapatkan,
$$n_{v_0} =\frac{2v_c^2}{c^2}\frac{dv_c}{e^{hv/kT}-1}\frac{1}{(1+z)^3}=\frac{2v_0^2}{c^2}\frac{dv_c}{e^{hv/kT}-1}$$
Ini memberi kita Wien’s Law lagi dan dengan demikian dapat disimpulkan bahwa -
$$T(z) = T_0\frac{\lambda_0}{\lambda_e} = T_0(1+z)$$
Poin untuk Diingat
- Alam semesta awal sangat panas, ∼ 3000K.
- Pengukuran saat ini mengungkapkan suhu alam semesta mendekati 3K.
- Semakin jauh ke masa lalu, suhu meningkat secara proporsional.
Pada bab ini, kita akan membahas anisotropi Radiasi CMB dan COBE, yaitu Cosmic Background Explorer.
Anisotropi Primer di CMB
Untuk memahami pengamatan dari luar angkasa dan anisotropi primer pada Radiasi Latar Belakang Gelombang Mikro Kosmik, mari kita ambil persamaan berikut dan memahaminya seperti gambar di bawah ini.
Kerapatan Nomor Foton CMB (n γ , 0)
$$n_{\gamma,0} = \frac{Total \: energy \: density}{Characteristic \: energy \:of \:Photons}$$
$$n_{\gamma,0} = \frac{aT_0^4}{k_BT_0}$$
Dimana $k_B$ adalah Boltzmann Constant dan $T_0$ adalah present temperature of the universe.
Menggunakan suhu saat ini $(T_0)$sebagai 2,7 K, kita mendapatkan kerapatan bilangan foton CMB saat ini sebagai 400 cm −3 .
Kerapatan bilangan foton bintang kosmik jauh lebih kecil (∼ = 10 −3 cm −3 ) pada skala besar.
Rasio Baryon ke Foton (η)
Jika kontribusi bintang dari galaksi, yang bercampur dengan CMB, dapat diabaikan, rasio baryon terhadap proton adalah -
$$\eta = \frac{n_{b,0}}{n_{\gamma,0}}$$
Nilai sekarang adalah ∼5 × 10 −10 . Karena kepadatan bilangan foton dan baryon sebanding dengana−3, kemudian η tidak berkembang seiring waktu.
Kepadatan Energi
Berbeda dengan kerapatan bilangan, kerapatan energi materi lebih didominasi daripada kerapatan energi foton saat ini.
Kepadatan energi materi baryonic = $\rho_{b,0}c^2 = 0.04\rho_cc^2 = 2 × 10^{−9} ergcm^{−3}$. Sedangkan kepadatan energi radiasi =$aT_0^4 = 4 \times 10^{−13}ergcm{−3}$.
Isotropi Radiasi CMB
Penzias dan Wilsonmenemukan CMB menjadi isotropik dalam batas-batas pengamatan. Batasannya adalah resolusi sudut rendah dan sensitivitas instrumen. Mereka melakukan pengamatan dari bumi, karena itu, pengamatan tidak dapat dilakukan melalui semua spektrum karena uap air di atmosfer menyerap banyak panjang gelombang mulai dari 1mm hingga 1m. Jadi, CMB tidak bisa dianggap sebagai spektrum.
CMB dianggap invarian secara rotasi (isotropik). Karena ada masa ketika materi dan radiasi berada dalam kesetimbangan, maka pembentukan struktur di alam semesta tidak dapat dijelaskan. Karena distribusi materi bukanlah isotropik tetapi berkumpul bersama seperti jaring kosmik dengan rongga besar di antaranya, CMB dianggap memiliki asal ekstragalaktik.
Tetapi, ketika pengamatan dari ruang angkasa dimulai, anisotropi di CMB ditemukan, yang mengarah pada alasan bahwa anisotropi ini dalam materi mengarah pada pembentukan struktur.
Pengamatan Radiasi CMB dari Luar Angkasa
Satelit utama yang diluncurkan untuk mengamati CMB adalah -
Cosmic Microwave Background Explorer (COBE, 1989)
Wilkinson Microwave Anisotropy Probe (WMAP, 2001) dan
Planck (2009).
COBE (Penjelajah Latar Belakang Kosmik)
COBE memiliki dua instrumen. MerekaFar InfraRed Absolute Spectrometer (FIRAS) dan Differential Microwave Radiometers(Antena DMR). FIRAS mengukur intensitas CMB sebagai fungsi panjang gelombang sepanjang arah tertentu. Sedangkan DMR memiliki 3 antena untuk mengukur perbedaan intensitas CMB dari tiga arah yang berbeda. Petunjuk berikut memberi kita beberapa informasi lebih lanjut tentang FIRAS dan DMR.
Pengamatan CMB dari FIRAS menunjukkan bahwa radiasi CMB sesuai dengan spektrum benda hitam pada T = 2.72528 ± 0.00065 K.
DMR mengukur tiga frekuensi (31,5 GHz, 53 GHz, 90 GHz) ke segala arah di langit.
The “red batman symbol” pada pengamatan DMR adalah noise dari emisi latar depan (emisi synchrotron difusi galaksi).
Variasi intensitas dalam pengamatan sesuai dengan variasi suhu. Adanya titik panas dan dingin membuktikan bahwa radiasi CMB bersifat anisotropik.
Anisotropi ini harus ada pada waktu decoupling karena tidak ada distorsi pada CMB. Jadi, materi harus memiliki beberapa kantong dengan kepadatan yang lebih tinggi daripada kantong lainnya.
Hasil COBE
Spektrum CMB (intensitas sebagai fungsi energi) hampir merupakan benda hitam sempurna sesuai dengan T = 2,7 K. Intensitas spesifik radiasi CMB hampir sama untuk semua arah. Konfirmasi bahwa alam semesta isotropik dalam skala besar (memvalidasi asumsi prinsip kosmologis kami).
Analisis data menunjukkan bahwa terdapat anisotropi suhu (“fluktuasi”) dalam spektrum CMB pada resolusi COBE (DMR).
Resolution of COBE, WMAP, Planck
Instrumen DMR on-board COBE memiliki resolusi spasial (maksimum) terbatas ∼ 7 derajat.
Wilkinson Microwave Anisotropy Probe (WMAP) memiliki resolusi rata-rata ∼ 0,7 derajat.
Satelit Planck memiliki resolusi sudut ∼ 10 arc-minute.
Poin untuk Diingat
Kerapatan bilangan foton bintang kosmik jauh lebih kecil daripada kerapatan bilangan foton CMB.
Kita hidup di alam semesta yang didominasi materi, karena kepadatan energi materi lebih tinggi daripada kepadatan energi foton.
COBE, WMAP, Planck adalah upaya untuk mengukur dan mengkuantifikasi anisotropi di CMB.
Pembentukan struktur di alam semesta merupakan hasil anisotropi CMB.
Ketika kita melihat pada peta CMB langit yang telah diperbaiki dan dikoreksi, ada banyak kontaminasi latar depan, yang merupakan semacam anisotropydi peta ini. Kita dapat melihat bahwa emisi latar depan ini berasal dari galaksi bima sakti. Intensitas CMB tinggi di sepanjang bidang bidang galaksi dan berkurang intensitasnya saat kita menjauh. Di sini, kita dapat mengamati anisotropi sekunder, yang merupakan emisi synchrotron dari galaksi. Emisi ini membentuk kontaminasi latar depan. Untuk melihat emisi CMB dari langit, kita perlu mengurangi emisi latar depan ini.
Gambar berikut menunjukkan CMB dengan emisi latar depan.

Anisotropi Dipol
Ada jenis anisotropi lain, yang ditemukan di CMB all sky map, disebut sebagai Dipole Anisotropy. Itu tidak terkait dengan alam semesta awal. Ini dapat direpresentasikan menggunakan fungsi harmonik bola. Jika terdapat pola pada permukaan bola dan kita ingin memetakannya menggunakan fungsi matematika, kita dapat melakukannya dengan menggunakan fungsi trigonometri. Jadi, saat kita memetakan, itu bisa menjadi monopole - sama di setiap arah, atau dipol - membalik properti saat diputar 180 derajat. Demikian pula, kita memiliki quadrupole dan seterusnya. Untuk pola yang kompleks, ini dapat dinyatakan sebagai jumlah monopole, dipole, quadrupole, dll.
CMB dimodelkan sedemikian rupa sehingga salah satu sumber utama anisotropi di semua peta langit adalah anisotropi dipol ini, tetapi ini bukan pemodelan CMB primordial. Hal tersebut dapat dilihat pada gambar di bawah ini.

Arah dipol yang kita lihat bukanlah arah yang acak. Anisotropi dipol memiliki arah. Kami melihat intensitas CMB di sepanjang arah tertentu. Arah ini disebabkan oleh vektor kecepatan tata surya. Kecepatan bumi dapat direpresentasikan sehubungan dengan matahari atau pusat galaksi. Arah pergerakan bumi, kami mengamati pergeseran biru dan pergeseran merah dan dipol terletak di sepanjang arah ini.
Gambar di atas memiliki tampilan dipol yang khas karena galaksi kita bergerak ke arah tertentu. Hasilnya - satu sisi langit akan muncul Redshifted dan sisi lain langit akan muncul Blueshifted. Dalam hal ini, Pergeseran Merah berarti foton lebih panjang dalam panjang gelombang = lebih dingin (jadi mundur dari namanya, foton tampak biru pada diagram di atas).
Kita dapat mengatakan, bumi sedang bergerak ke beberapa arah tertentu sehubungan dengan matahari / pusat galaksi / CMB di langit pada saat tertentu. Kemudian, jika kita melihat pada sudut mana pun dan mengukur suhu CMB, hasilnya akan berbeda. Ini karena, kami mengukur foton yang tergabung dalam Blueshifted atau Redshifted dan bergantung pada garis pandang foton di langit.
Poin untuk Diingat
Kontaminasi latar depan CMB semua peta langit disebut anisotropi CMB.
Emisi ini berasal dari galaksi bima sakti kita.
2 jenis anisotropi adalah: Anisotropi Dipol dan Anisotropi Spektrum Daya Sudut.
Anisotropi dipol berada pada arah tertentu, sedangkan anisotropi Angular Power Spectrum tersebar di mana-mana.
Panjang Horizon adalah jarak yang ditempuh oleh foton cahaya dari 'The Big Bang' ke 'The Recombination Era'. 1 st puncak spektrum sudut adalah pada θ = 1◦ (l = 180), yang merupakan skala panjang sangat istimewa.
Jarak yang tepat antara dua titik diberikan oleh -
$$r_p = \int_{0}^{t}cdt$$
Jika kita ambil time frame dari t = 0 ke t = t rec , maka
$$r_H = \int_{0}^{t_{rec}}cdt$$
Dimana $r_H$ adalah jarak horizon yang tepat.
Sekarang, kita tahu bahwa -
$$\dot{a} = \frac{\mathrm{d} a}{\mathrm{d} t}$$
$$dt = \frac{da}{\dot{a}}$$
Saat t = 0, a = 0.
Kemudian $t = t_{rec}, a = a_0 / (1 + z_{rec})$.
Karenanya, kami dapat menulis,
$$r_H(z_{rec})=\int_{0}^{a_{rec}} c\frac{da}{aH}$$
$$H(a_{rec}) = H(z_{rec}) = H_0\sqrt{\Omega_{m,0}}a^{-3/2}$$
Selama Recombination period universeadalah materi yang didominasi. yaitu,Ωrad << Ωmatter. Oleh karena itu, istilah radiasi dijatuhkan.
$$r_H(z_{rec}) = \frac{c}{H_0\sqrt{\Omega_{m,0}}}\int_{0}^{a_{rec}} \frac{da}{a^{-1/2}}$$
$$r_H(z_{rec}) = \frac{2c}{3H_0\sqrt{\Omega_{m,0}}}\frac{1}{(1+z_{rec})^{3/2}}$$
$$\theta_H(rec) = \frac{r_H(z_{rec})}{d_A(z_{rec})}$$
Yang sama dengan 0,5 derajat, jika kita memasukkan semua nilai yang diketahui ke dalam persamaan.
Itu Electromagnetic radiationburam dari permukaan hamburan terakhir. Dua titik mana pun yang 'tidak' terletak di dalam cakrawala satu sama lain tidak perlu memiliki sifat yang sama. Sehingga akan memberikan nilai temperatur yang berbeda.
Kita bisa mendapatkan dua titik di permukaan ini yang tidak saling berpotongan, yang berarti pada satu titik alam semesta mengembang lebih cepat dari kecepatan cahaya yang merupakan model inflasi untuk ekspansi.
Poin untuk Diingat
Panjang cakrawala adalah jarak yang ditempuh foton cahaya dari 'Ledakan Besar' ke 'Era Rekombinasi'.
Selama periode Rekombinasi, alam semesta didominasi materi.
Radiasi elektromagnetik tidak tembus cahaya dari permukaan hamburan terakhir.
Astrobiologyadalah studi tentang asal-usul, evolusi, distribusi, dan masa depan kehidupan di alam semesta. Ini berkaitan dengan menemukan dan mendeteksiExtrasolar Planets.
Astrobiology membahas poin-poin berikut -
Bagaimana kehidupan dimulai dan berkembang? (biologi + geologi + kimia + ilmu atmosfer)
Apakah ada dunia di luar bumi yang menguntungkan bagi kehidupan? (astronomi)
Bagaimana masa depan kehidupan di bumi?
Astronomy membahas poin-poin berikut -
Bagaimana cara mendeteksi sistem planet di sekitar bintang lain?
Salah satu metodenya adalah pencitraan langsung, tetapi ini adalah tugas yang sangat sulit karena planet merupakan sumber cahaya yang sangat redup dibandingkan dengan bintang, dan sedikit cahaya yang berasal darinya cenderung hilang dalam silau dari bintang induknya.
Kontras lebih baik bila planet lebih dekat dengan bintang induk dan panas, sehingga memancarkan radiasi infra merah yang intens. Kami dapat membuat gambar di wilayah inframerah.
Teknik untuk Deteksi Planet Ekstra Surya
Teknik yang paling efisien untuk deteksi planet ekstrasurya adalah sebagai berikut. Masing-masing juga dijelaskan secara rinci pada bab-bab selanjutnya.
Metode Kecepatan Radial
Ini juga disebut sebagai metode Doppler. Dalam hal ini -
Sistem planet bintang berputar di sekitar barycenter mereka, goyangan bintang.
Goyangan dapat dideteksi dengan
Pergeseran Merah / Biru berkala. Astrometri - mengukur objek di langit dengan sangat tepat.
Metode Transit
Metode Transit (teleskop luar angkasa Kepler) digunakan untuk mengetahui besarnya. Penurunan kecerahan bintang per planet biasanya sangat kecil, tidak seperti dalam sistem biner.
Pencitraan Langsung
Pencitraan planet menggunakan teleskop.
Mari kita lihat studi kasus yang dilakukan pada Metode Kecepatan Radial.
Studi kasus
Studi kasus ini adalah pada orbit Circular dan bidang orbit tegak lurus dengan bidang langit. Waktu yang dibutuhkan oleh keduanya di sekitar barycenter akan sama. Ini akan sama dengan perbedaan waktu antara dua Redshift atau Blueshift.
Perhatikan gambar berikut.

Pada A dan C - kecepatan penuh diukur. Di C, kecepatan adalah nol.
Vrmax = V * adalah kecepatan sebenarnya dari bintang.
P adalah periode waktu bintang dan juga planet.
θ adalah fase orbit.
Massa Bintang - M * , radius Orbit a * , massa planetmp.
Dari pusat persamaan massa,
$$m_p a_p = M_\ast a_\ast$$
Dari persamaan kecepatan,
$$V_\ast = \frac{2\pi a_\ast}{P}$$
$$\Rightarrow a_\ast = \frac{PV_\ast}{2\pi}$$
Dari Kepler’s Law,
$$P^2 = \frac{4\pi^2a_p^3}{GM_\ast}$$
$$\Rightarrow a_p = \left ( \frac{P^2GM_\ast}{4\pi^2} \right)^{1/3}$$
Dari persamaan di atas, kita dapatkan -
$$\Rightarrow m_p = \left( \frac{P}{2\pi G} \right)^{1/3}M_\ast^{2/3}V_\ast$$
Kita mendapatkan: $m_p, a_p$ dan $a_\ast$.
Persamaan di atas bias terhadap sebagian besar planet masif yang dekat dengan bintang.
Poin untuk Diingat
Astrobiologi adalah studi tentang asal usul, evolusi, distribusi, dan masa depan kehidupan di alam semesta.
Teknik untuk mendeteksi planet ekstrasurya adalah: Metode Kecepatan Radial, Metode Transit, Pencitraan Langsung, dll.
Goyangan dapat dideteksi dengan pergeseran merah / biru berkala dan Astrometri.
Metode Kecepatan Radial bias untuk mendeteksi planet masif yang dekat dengan bintang.
Pada bab sebelumnya, Metode Kecepatan Radial untuk kasus di mana bidang orbit dan bidang langit tegak lurus telah dibahas untuk orbit melingkar. Di sini, kita akan membahas satu kasus lagi, ketika bidang orbit dan bidang langit tidak tegak lurus untuk orbit melingkar.
Ketika bidang orbit berada pada sudut terhadap bidang langit (tidak tegak lurus), kita mendapatkan situasi berikut -

Dalam kasus ini, ketika keduanya tegak lurus, kami memiliki dua titik di mana kami dapat mengukur kecepatan sebenarnya. Tapi di sini, itu tidak mungkin. Pada semua titik, kita hanya dapat mengukur komponen kecepatan sebenarnya,v.
$$v_r = v \:sin(i)cos(\theta)$$
dimana θadalah fase orbit yang merupakan besaran yang bergantung pada waktu. Sudut kemiringanidi sisi lain, tidak bergantung pada waktu. Karenanya,
$$(v_r)_{max} = v\: sin(i)$$
Kurva kecepatan radial yang diamati akan berbentuk berikut -

Ketika bidang orbit tegak lurus dengan langit -
$$m_p = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}}(M_\ast)^{\frac{2}{3}}v$$
dimana mp, P, G, M∗adalah massa planet, periode orbit, konstanta gravitasi universal, dan massa bintang. Tetapi dalam kasus ini, kita harus memodifikasinya sebagai berikut -
$$m_psin(i) = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}} (M_\ast)^{\frac{2}{3}}(v_r)_{max}$$
Namun, menemukan nilai i adalah tugas yang sulit. Kami dapat memberlakukan batasan tertentu pada nilaiimenggunakan metode transit. Lintasan planet antara bintang dan bumi disebut transit. Kita dapat memperoleh kurva cahaya dengan mengamati transit dan penurunan signifikan pada fluks yang diamati dari kurva cahaya menunjukkan bahwa i mendekati 90 derajat. Jika kondisi seperti itu tidak dipenuhi, kami tidak dapat mengetahui nilai darii. Kemudian nilaimp yang kami temukan dapat berfungsi sebagai batas bawah massa planet, karena memang demikian mp sin(i) dan sin(i) ≤ 1.
Kesimpulannya, metode kecepatan radial lebih nyaman daripada metode transit karena kecepatan radial dapat diukur setiap saat tetapi pengukuran transit hanya dapat dilakukan selama transit yang mungkin tidak berlangsung lama.
Poin untuk Diingat
Menemukan kemiringan orbit planet tidak dilakukan dengan metode Kecepatan Radial.
Metode Kecepatan Radial lebih baik daripada Metode Transit karena kecepatan radial dapat diukur selalu tidak seperti metode transit.
Transit berumur pendek dan sangat mudah untuk dilewatkan.
Metode Transit (Kepler Space Telescope)digunakan untuk mengetahui ukurannya. Penurunan kecerahan bintang oleh sebuah planet biasanya sangat berbeda dengan sistem biner.
F0 adalah fluks bintang sebelum planet itu menggantikannya.
F1 adalah fluks setelah seluruh planet berada di depan bintang.
Gambar berikut akan digunakan untuk semua perhitungan.

$$\frac{F_0 - F_1}{F_0} = \frac{\pi r_p^{2}}{\pi R^2_\ast}$$
$$\frac{\Delta F}{F} \cong \frac{r^2_p}{R^2_\ast}$$
$$\left ( \frac{\Delta F}{F} \right )_{earth} \cong 0.001\%$$
$$\left ( \frac{\Delta F}{F} \right )_{jupiter} \cong 1\%$$
Ini tidak mudah dicapai dengan teleskop berbasis darat. Ini dicapai oleh teleskop Hubble.

Sini, $t_T$ adalah waktu antara posisi A dan D dan $t_F$ adalah waktu antara posisi B dan C.
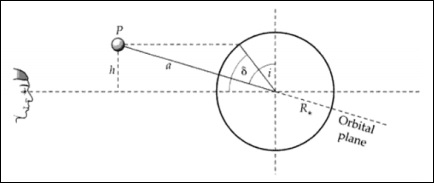
Geometri transit terkait dengan kemiringan idari sistem. Garis lintang dan kemiringan transit dapat dipertukarkan.
Dari gambar di atas, kita bisa menulis -
$$\frac{h}{a} = cos(i)$$
$$\frac{h}{R_\ast} = sin(\delta)$$
$$cos(i) = \frac{R_\ast sin(\delta)}{a}$$
$$y^2 = (R_\ast + R_p)^2 - h^2$$
$$y = [(R_\ast + R_p)^2 - h^2]^{\frac{1}{2}}$$
$$sin(\theta) = \frac{y}{a}$$
$$\theta = sin^{-1}\left [ \frac{(R_\ast + R_p)^2 - a^2cos^2(i)}{a^2} \right ]^{\frac{1}{2}}$$
$$t_T = \frac{P}{2\pi} \times 2\theta$$
Sini, $t_T$ adalah pecahan dari periode waktu terjadinya transit dan (2θ / 2π) adalah pecahan sudut terjadinya transit.
$$sin(\frac{t_T\pi}{P}) = \frac{R_\ast}{a}\left [ \left ( 1+ \frac{R_p}{R_\ast}\right )^2 - \left ( \frac{a}{R_\ast}cos(i)\right )^2 \right ]^{\frac{1}{2}}$$
Biasanya, a >> R ∗ >> Rp. Jadi, kita bisa menulis -
$$sin(\frac{t_T\pi}{P}) = \frac{R_\ast}{a}\left [ 1- \left ( \frac{a}{R_\ast}cos(i) \right )^2\right ]^{\frac{1}{2}}$$
Sini, Padalah durasi antara dua transit berturut-turut. Waktu transit sangat kurang dibandingkan dengan periode waktu orbit. Karenanya,
$$t_T = \frac{P}{\pi}\left [ \left ( \frac{R_\ast}{a}\right )^2 - cos^2(i)\right ]^{\frac{1}{2}}$$
Sini, tT, P, R∗ adalah yang bisa diamati, a dan i harus ditemukan.
Sekarang,
$$sin(\frac{t_F\pi}{P}) = \frac{R_\ast}{a}\left [\left (1 - \frac{R_p}{R_\ast} \right )^2 - \left ( \frac{a}{R_\ast}cos\:i \right )^2\right ]^{\frac{1}{2}}$$
dimana, $y^2 = (R_\ast − R_p)^2 − h^2$.
Membiarkan,
$$\frac{\Delta F}{F} = D = \left ( \frac{R_p}{R_\ast} \right )^2$$
Sekarang, kita bisa mengungkapkan,
$$\frac{a}{R_\ast} = \frac{2P}{\pi} D^{\frac{1}{4}}(t^2_T - t^2_F)^{-\frac{1}{2}}$$
Untuk bintang deret utama,
$$R_\ast \propto M^\alpha_\ast$$
$$\frac{R_\ast}{R_0} \propto \left ( \frac{M_\ast}{M_0}\right )^\alpha$$
Ini memberi R∗.
Karenanya, kami mendapatkan nilai 'a' juga.
Jadi, kita mendapatkan 'R p ', 'ap' dan bahkan 'i'.
Untuk semua ini,
$$h \leq R_\ast + R_p$$
$$a\: cos\: i \leq R_\ast + R_p$$
Bahkan ~ 89 derajat, durasi transit sangat kecil. Planet tersebut harus sangat dekat untuk mendapatkan waktu transit yang cukup. Ini memberikan batasan yang ketat pada 'i'. Begitu kita mendapatkan 'i', kita bisa mendapatkan 'm p ' dari pengukuran kecepatan radial.
Deteksi dengan metode transit ini disebut sebagai deteksi peluang, yaitu probabilitas mengamati transit. Perhitungan probabilitas transit (probabilitas pengamatan) ditunjukkan di bawah ini.
Probabilitas transit terkait dengan sudut padat yang dilacak oleh dua konfigurasi transit ekstrim, yaitu -
$$Solid \: angle \:of \:planet \: = 2\pi \left ( \frac{2R_\ast}{a} \right )$$
Serta total sudut solid pada sumbu semi-mayor a, atau -
$$Solid \:angle \:of \:sphere \: =\: 4\pi$$
Probabilitasnya adalah rasio dari dua area ini -
$$= \: \frac{area \:of\: sky \: covered \:by\: favourable \: orientation}{area\: of\: sky \:covered\: by\: all\: possible\: orientation\: of\: orbit}$$
$= \frac{4\pi a_pR_\ast}{4\pi a^2_p} = \frac{R_\ast}{a_p}$ $\frac{area\: of\: hollow \: cyclinder}{area\: of\: sphere}$
Probabilitas ini tidak tergantung pada pengamat.
Poin untuk Diingat
- Metode Transit (Teleskop Luar Angkasa Kepler) digunakan untuk mengetahui ukurannya.
- Deteksi dengan Metode Transit adalah deteksi kebetulan.
- Planet tersebut harus sangat dekat untuk mendapatkan waktu transit yang cukup.
- Probabilitas transit terkait dengan sudut padat planet.
- Probabilitas ini tidak tergantung pada kerangka acuan pengamat.
Gambar langsung pertama dari planet ekstrasurya, pada tahun 2004, adalah sebuah planet bermassa 3-10 Mjupiter mengorbit di sekitar katai coklat (2M1207) bermassa 25 Mjupiter. Teknik seperti kecepatan Radial, Transit, microlensing gravitasi, Pencitraan, Astrometri, dll., Telah digunakan untuk mendeteksi exoplanet. Jumlah deteksi meningkat setiap tahun.
Hingga sekitar tahun 2010, metode kecepatan Radial digunakan secara luas, namun saat ini sebagian besar pendeteksian dilakukan dengan metode Transit. Ada lonjakan dalam jumlah deteksi pada tahun 2014, saat itulahKepler Space Telescope (KST) mulai memberikan hasil.
Distribusi periode massa menunjukkan bahwa metode kecepatan Radial lebih condong ke arah deteksi planet masif dengan periode lebih besar, sedangkan dengan metode Transit, planet dengan periode lebih rendah hanya terdeteksi seperti yang ditunjukkan pada gambar berikut (Courtesy: NASA Exoplanet Archive) .
Ada peningkatan kolosal dalam jumlah deteksi planet bermassa lebih kecil sejak munculnya KST. Ini terbukti dari gambar yang diberikan di bawah ini. Planet yang terdeteksi oleh KST dibagi menjadi dua kelompok: planet masif panas yang disebut "Jupiter Panas" dan planet bermassa lebih rendah yang disebut "Bumi Super Panas" (karena lebih masif dari Bumi).

Saat kami memplot jumlah planet ekstrasurya yang terdeteksi versus jaraknya, kami menemukan bahwa sebagian besar planet ini berada dalam jarak 2kpc, yang berada di dalam galaksi kita. Mungkin planet-planet bukan hal yang aneh di alam semesta, karena deteksi kita terbatas hanya pada jenis planet tertentu di sebagian kecil alam semesta.
Planet terbentuk dari circumstellar disc atau proto planetary disc. Jika planet terbentuk sebagai produk sampingan selama pembentukan bintang, mungkin jumlah planet di alam semesta melebihi jumlah bintang di alam semesta !!
Zona Hunian
Zona Hunian dapat didefinisikan sebagai zona di sekitar bintang tempat air dapat berada dalam bentuk cairnya. Pertimbangkan planet di kejauhan$a_p$dari bintang seperti yang ditunjukkan pada gambar berikut. Metode sederhana untuk menghitung suhu planet dijelaskan sebagai berikut.
$$\left ( \frac{L_\ast}{4\pi a^2_p} \right )\pi R^2_p(1 - A) = 4\pi R^2_p \sigma T^4_p$$
dan
$$\frac{L_\ast}{4\pi R^2_\ast} = \sigma T^4_\ast$$
$$\therefore T_p = (1 - A)T_\ast \sqrt{\frac{R_\ast}{2a_p}}$$
Dalam kasus kami, mengganti
Lsun = 3.83 x 1026
ap = 1.5 ∗ 1011 and
A = 0.3
Akan memberi $T_{Earth} = 255K$. Perhitungan sebenarnya sangat terlibat termasuk fisika awan. Zona layak huni di tata surya kita terletak antara 0,9 AU dan 1,7 AU.
Luminositas Matahari ditemukan meningkat seiring waktu karena tekanan gas yang menurun. Itu 30% kurang terang saat mulai membakar hidrogen. Hal ini akan mengakibatkan pergeseran zona layak huni menjauhi Matahari. Karena Bumi berada di dekat tepi dalam zona Hunian, mungkin suatu hari Bumi akan keluar dari zona tersebut!
Zona Layak Huni
Singkatnya itu disebut sebagai CHZdapat didefinisikan sebagai wilayah di mana air cair dapat berada selama seluruh masa Urutan Utama sebuah bintang. KST telah mendeteksi banyak planet ekstrasurya yang terletak di zona layak huni.
Tanda tangan biologis adalah zat apa pun - seperti unsur, isotop, molekul, atau fenomena yang memberikan bukti ilmiah kehidupan masa lalu atau masa kini. Contohnya adalah deteksi O 2 dan CO 2 di planet, yang biasanya tidak mungkin dilakukan melalui proses geologi saja. Deteksi ini dilakukan dengan menganalisis spektrum serapan.
Poin untuk Diingat
Teknik seperti kecepatan Radial, Transit, microlensing gravitasi, Pencitraan, Astrometri, dll., Telah digunakan untuk mendeteksi exoplanet.
Metode kecepatan radial lebih condong pada deteksi planet masif dengan periode lebih besar.
Planet masif panas disebut "Jupiter Panas" dan planet bermassa lebih rendah disebut "Bumi Super Panas".
Jumlah planet di alam semesta melebihi jumlah bintang di alam semesta.
Zona layak huni dapat didefinisikan sebagai zona di sekitar bintang tempat air dapat berada dalam bentuk cairnya.