Kosmologi - Metode Transit
Metode Transit (Kepler Space Telescope)digunakan untuk mengetahui ukurannya. Penurunan kecerahan bintang oleh sebuah planet biasanya sangat berbeda dengan sistem biner.
F0 adalah fluks bintang sebelum planet itu menggantikannya.
F1 adalah fluks setelah seluruh planet berada di depan bintang.
Gambar berikut akan digunakan untuk semua perhitungan.

$$ \ frac {F_0 - F_1} {F_0} = \ frac {\ pi r_p ^ {2}} {\ pi R ^ 2_ \ ast} $$
$$ \ frac {\ Delta F} {F} \ cong \ frac {r ^ 2_p} {R ^ 2_ \ ast} $$
$$ \ kiri (\ frac {\ Delta F} {F} \ kanan) _ {bumi} \ cong 0,001 \% $$
$$ \ kiri (\ frac {\ Delta F} {F} \ kanan) _ {jupiter} \ cong 1 \% $$
Ini tidak mudah dicapai dengan teleskop berbasis darat. Ini dicapai oleh teleskop Hubble.

Di sini, $ t_T $ adalah waktu antara posisi A dan D dan $ t_F $ adalah waktu antara posisi B dan C.
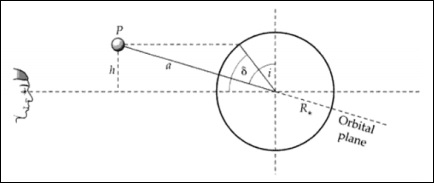
Geometri transit terkait dengan kemiringan idari sistem. Garis lintang dan kemiringan transit dapat dipertukarkan.
Dari gambar di atas, kita bisa menulis -
$$ \ frac {h} {a} = cos (i) $$
$$ \ frac {h} {R_ \ ast} = sin (\ delta) $$
$$ cos (i) = \ frac {R_ \ ast sin (\ delta)} {a} $$
$$ y ^ 2 = (R_ \ ast + R_p) ^ 2 - j ^ 2 $$
$$ y = [(R_ \ ast + R_p) ^ 2 - j ^ 2] ^ {\ frac {1} {2}} $$
$$ sin (\ theta) = \ frac {y} {a} $$
$$ \ theta = sin ^ {- 1} \ kiri [\ frac {(R_ \ ast + R_p) ^ 2 - a ^ 2cos ^ 2 (i)} {a ^ 2} \ kanan] ^ {\ frac {1 } {2}} $$
$$ t_T = \ frac {P} {2 \ pi} \ times 2 \ theta $$
Di sini, $ t_T $ adalah pecahan dari periode waktu terjadinya transit dan (2θ / 2π) adalah pecahan sudut terjadinya transit.
$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ kiri [\ kiri (1+ \ frac {R_p} {R_ \ ast} \ kanan) ^ 2 - \ kiri (\ frac {a} {R_ \ ast} cos (i) \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$
Biasanya, a >> R ∗ >> Rp. Jadi, kita bisa menulis -
$$ sin (\ frac {t_T \ pi} {P}) = \ frac {R_ \ ast} {a} \ kiri [1- \ kiri (\ frac {a} {R_ \ ast} cos (i) \ kanan ) ^ 2 \ kanan] ^ {\ frac {1} {2}} $$
Sini, Padalah durasi antara dua transit berturut-turut. Waktu transit sangat kurang dibandingkan dengan periode waktu orbit. Karenanya,
$$ t_T = \ frac {P} {\ pi} \ kiri [\ kiri (\ frac {R_ \ ast} {a} \ kanan) ^ 2 - cos ^ 2 (i) \ kanan] ^ {\ frac {1 } {2}} $$
Sini, tT, P, R∗ adalah yang bisa diamati, a dan i harus ditemukan.
Sekarang,
$$ sin (\ frac {t_F \ pi} {P}) = \ frac {R_ \ ast} {a} \ kiri [\ kiri (1 - \ frac {R_p} {R_ \ ast} \ kanan) ^ 2 - \ kiri (\ frac {a} {R_ \ ast} cos \: i \ right) ^ 2 \ right] ^ {\ frac {1} {2}} $$
di mana, $ y ^ 2 = (R_ \ ast - R_p) ^ 2 - h ^ 2 $.
Membiarkan,
$$ \ frac {\ Delta F} {F} = D = \ kiri (\ frac {R_p} {R_ \ ast} \ kanan) ^ 2 $$
Sekarang, kita bisa mengungkapkan,
$$ \ frac {a} {R_ \ ast} = \ frac {2P} {\ pi} D ^ {\ frac {1} {4}} (t ^ 2_T - t ^ 2_F) ^ {- \ frac {1 } {2}} $$
Untuk bintang deret utama,
$$ R_ \ ast \ propto M ^ \ alpha_ \ ast $$
$$ \ frac {R_ \ ast} {R_0} \ propto \ kiri (\ frac {M_ \ ast} {M_0} \ kanan) ^ \ alpha $$
Ini memberi R∗.
Karenanya, kami mendapatkan nilai 'a' juga.
Jadi, kita mendapatkan 'R p ', 'ap' dan bahkan 'i'.
Untuk semua ini,
$$ h \ leq R_ \ ast + R_p $$
$$ a \: cos \: i \ leq R_ \ ast + R_p $$
Bahkan ~ 89 derajat, durasi transit sangat kecil. Planet tersebut harus sangat dekat untuk mendapatkan waktu transit yang cukup. Ini memberikan batasan yang ketat pada 'i'. Begitu kita mendapatkan 'i', kita bisa mendapatkan 'm p ' dari pengukuran kecepatan radial.
Deteksi dengan metode transit ini disebut sebagai deteksi peluang, yaitu probabilitas mengamati transit. Perhitungan probabilitas transit (probabilitas pengamatan) ditunjukkan di bawah ini.
Probabilitas transit terkait dengan sudut padat yang dilacak oleh dua konfigurasi transit ekstrim, yaitu -
$$ Padat \: sudut \: dari \: planet \: = 2 \ pi \ kiri (\ frac {2R_ \ ast} {a} \ kanan) $$
Serta total sudut solid pada sumbu semi-mayor a, atau -
$$ Padat \: sudut \: dari \: bola \: = \: 4 \ pi $$
Probabilitasnya adalah rasio dari dua area ini -
$$ = \: \ frac {area \: dari \: langit \: tertutup \: oleh \: disukai \: orientasi} {area \: dari \: langit \: tertutup \: oleh \: semua \: mungkin \: orientasi \: dari \: orbit} $$
$ = \ frac {4 \ pi a_pR_ \ ast} {4 \ pi a ^ 2_p} = \ frac {R_ \ ast} {a_p} $ $ \ frac {area \: dari \: hollow \: cyclinder} {area \ : dari \: sphere} $
Probabilitas ini tidak tergantung pada pengamat.
Poin untuk Diingat
- Metode Transit (Teleskop Luar Angkasa Kepler) digunakan untuk mengetahui ukurannya.
- Deteksi dengan Metode Transit adalah deteksi kebetulan.
- Planet tersebut harus sangat dekat untuk mendapatkan waktu transit yang cukup.
- Probabilitas transit terkait dengan sudut padat planet.
- Probabilitas ini tidak tergantung pada kerangka acuan pengamat.