추론-시계
시계의 손 (180)의 최대 각도 할 수 있습니다 오 그들 사이. 이 경우 양손은 직선을 나타냅니다.
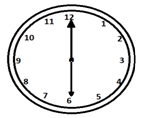
시계 바늘은 서로 15 분 거리에있을 때 매시간 두 번씩 직각을 만듭니다.
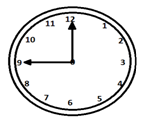
시계의 두 바늘은 매시간 한 번씩 일치합니다.
시계는 모든 인간이 일상 업무를 예약하는 데 매우 중요합니다. 시계 이론은 일상 생활과 관련이 있습니다.
시계는 시간을시, 분, 초로 나누어 시간을 표시하는 도구입니다.
다이얼
시간을 나타내는 1에서 12까지 번호가 매겨진 원형 다이얼이 있습니다. 다이얼의 둘레는 60 개의 동일한 공간으로 더 나뉘며이를 분 공간이라고합니다.
1 시간 = 60 분
1 분 = 60 초
1 시간 = 3600 초
트릭
n시와 (n + 1)시 사이에 시계의 두 바늘이 n시에서 $ \ left (\ frac {60n} {11} \ right) $ 분에서 일치합니다.
n시와 (n + 1)시 사이에, 시계의 두 바늘은 n을 지나서 $ \ left (5n \ pm 15 \ right) \ times \ frac {12} {11} $ min에서 서로 직각을 이룹니다. .
n시와 (n + 1)시 사이에 시계의 바늘이 (함께 있지 않고) 일직선이됩니다.
$ \ left (5n-30 \ right) \ times \ frac {12} {11} $ 분 지난 n, (n> 6 일 때)
$ \ left (5n + 30 \ right) \ times \ frac {12} {11} $ min 지난 n, (n <6 일 때)
n시와 (n + 1)시 사이에 시계 바늘은 $ \ left (5n \ pm x \ right) \ times \ frac {12} {11} $ 분에서 $ x $ 분 떨어져 있습니다. '+'기호는 분침이 앞에 있음을 나타내고 '–'기호는 시침이 앞에 있음을 나타냅니다.
시계의 분침이 올바른 시간의 $ x $ 분 간격으로 시침을 추월하면 시계가 $ \ left (\ frac {720} {11}-x \ right) \ left만큼 잃거나 증가합니다. (\ frac {60 \ times 24} {x} \ right) $ 분
1 − 7.15에서 8.15 사이에 시계 바늘이 서로 일치합니까?
Options −
A -$ 39 \ frac {5} {11} $
B -$ 39 \ frac {4} {11} $
C -$ 38 \ frac {5} {11} $
D -$ 39 \ frac {4} {11} $
Answer − A
Explanation −
$ \ frac {60 \ times n} {11} = \ frac {60} {11} \ times \ frac {29} {4} = 39 \ frac {5} {11} $
$ n = 7.15 = 7 \ frac {15} {60} = \ frac {29} {4} $
2 − 9시에서 8시 사이에 양손이 서로 직각을 이루는 특정 시간은 언제입니까?
Options −
A -9시 이후 $ 65 \ frac {4} {11} $ 및 $ 32 \ frac {7} {11} $ 분
B -9시 이후 $ 65 \ frac {2} {11} $ 및 $ 32 \ frac {2} {11} $ 분
C -9 분 후 $ 65 \ frac {3} {11} $ 및 $ 32 \ frac {3} {11} $ 분
D -9시 이후 $ 65 \ frac {1} {11} $ 및 $ 32 \ frac {1} {11} $ 분
Answer − A
Explanation −
$ \ left (5n \ pm 15 \ right) \ times \ frac {12} {11} = \ left (5 \ times9 \ pm 15 \ right) \ times \ frac {12} {11} $
$ = 65 \ frac {4} {11} $ 및 $ 32 \ frac {7} {11} $ 분 지난 9시
3 − 12시에서 1시 사이에 시계의 양침이 언제 직선을 이룹니 까?
Options −
A-$ \ frac {360} {11} $ 분 지난 12
B-$ \ frac {355} {11} $ 분 지난 12
C-$ \ frac {340} {11} $ 분 지난 12
D-$ \ frac {345} {11} $ 분 지난 12
Answer − D
Explanation −
$ \ left (5n-30 \ right) \ times \ frac {12} {11} $ 분 지난 n
$ \ left (6-30 \ right) \ times \ frac {12} {11} $ 분 지난 12
$ = \ frac {345} {11} $ 분 과거 12 (n = 12 이후)
4-얼마나 많은 시간에 시계 바늘이 30 분 안에있을 것입니다. 월요일 오후 12시에서 1시 사이에 공간이 떨어져 있습니까?
Options −
A -$ \ frac {1080} {11} $ 및 $ \ frac {300} {11} $ 분 지난 12시
B -$ \ frac {1080} {12} $ 및 $ \ frac {360} {11} $ 분 지난 12시
C -$ \ frac {1080} {11} $ 및 $ \ frac {360} {11} $ 분 지난 12시
D -$ \ frac {1080} {12} $ 및 $ \ frac {300} {12} $ 분 지난 12시
Answer − C
Explanation −
$ \ left (5n \ pm x \ right) \ times \ frac {12} {11} $
$ = \ 왼쪽 (5 \ times12 \ pm 30 \ 오른쪽) \ times \ frac {12} {11} $
$ = \ frac {90 \ times12} {11} $ 및 $ \ frac {30 \ times12} {11} $ 12시 이전 = $ \ frac {1080} {11} $ 및 $ \ frac {360} {11} 12시 $ 분
5− 시계의 분침이 61 분 간격으로 시침을 추월합니다. 그러면 시계는 얼마나 많은 시간을 잃거나 얻습니까?
Options −
A -$ 104 \ frac {4} {671} $ 분
B -$ 105 \ frac {1} {671} $ 분
C -$ 104 \ frac {3} {671} $ 분
D -$ 105 \ frac {4} {671} $ 분
Answer − B
Explanation −
$ \ left (\ frac {720} {11} -61 \ right) \ times \ left (\ frac {60 \ times24} {61} \ right) $
$ = 105 \ frac {1} {671} $ 분