추론-논리적 추론
논리적 추론은 다양한 경쟁 시험에이 장의 쉬운 및 마크 가져 오기 문제가 많이 포함되어 있으므로 중요한 장입니다. 이 장에서는 이러한 문제를 해결하는 두 가지 방법에 대해 설명합니다.
- 삼단 법
- 벤 다이어그램 방법
기초
문이 두 개 있으면 삼단 법이 문제를 해결하는 가장 좋은 방법이지만 문 수가 두 개 이상이면 벤 다이어그램 방법으로 이동합니다. 때때로 진술과 결론은 일반적으로 받아 들여지는 사실에서 파생되지만 논리적이지 않을 수도 있습니다. 예를 들면-
a) 일부 의자는 문입니다.
b) 모든 남자는 여자입니다
c) 우유가 흰색이 아닙니다.
결론에 도달하려면 추상적 사고가 필요합니다. 문장의 논리적 의미를 이해하고 그에 따라 결론에 답해야합니다. 각 진술은 사실로 생각해야하며 결론이 논리적으로 진술을 따르는 지 확인해야합니다.
예선
이것들은 한 가지가 다른 것과 얼마나 비슷하거나 다른지를 설명하는 데 사용되는 몇 가지 기본 단어입니다. 일부 한정자의 예는 "All", "Some", "Some-not"등입니다.
벤 다이어그램 개념
반면 벤 다이어그램은 기하학적 도형의 형태로 문장이나 문장을 표현할 수있는 과정입니다. 주어진 모든 진술은 가능한 벤 다이어그램에 그려져 있습니다. 그런 다음 모든 결론이 해당 다이어그램으로 확인됩니다. 모든 벤 다이어그램을 충족하는 결론은 유효한 결론으로 간주됩니다.
| 진술 | 해당 벤 다이어그램 |
|---|---|
| A는 모두 B |
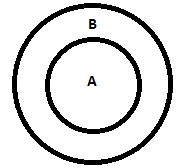
|
| 일부 A는 B (OR) 일부 A는 B가 아닙니다. |
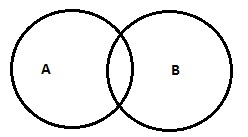
|
| 아니 A는 B |
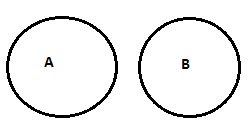
|
훨씬 더 나은 방식으로 이해하기 위해 간단한 예를 들어 봅시다.
Sample − 1
Statements −
모든 엔지니어는 바보입니다. 모든 바보는 의사입니다. 모든 의사는 가난합니다.
Conclusions −
I. 가난한 사람들은 바보입니다.
II. 가난한 사람들은 엔지니어입니다.
Options −
A − 나만 유효하다
B − II 만 유효합니다.
C − 두 진술 모두 유효 함
D − 유효한 진술이 없습니다.
Answer − 옵션 C
Explanation −
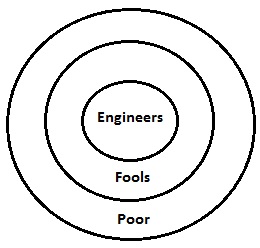
주어진 진술에 대한 벤 다이어그램은 위에 그려져 있습니다. 한 곳에서 모든 문장을 다이어그램으로 보여줍니다. 여기에서 결론에 대해 하나씩 논의하면 모든 것이 명확해질 것입니다.
여기서 바보는 가난한 사람들의 하위 집합입니다. 따라서 가난한 사람들이 바보가 될 것이라는 것은 분명한 사실입니다. 따라서 결론 I은 타당합니다. 마찬가지로 결론 II는 엔지니어가 가난한 사람들의 하위 집합이기 때문에 유효합니다. 따라서 두 진술 모두 유효합니다.
Sample − 2
Statements −
일부 키보드는 마우스입니다. 일부 마우스는 라디오입니다.
Conclusions −
I. 일부 키보드는 라디오입니다.
II. 일부 라디오는 키보드입니다.
III. 모든 라디오는 마우스입니다.
IV. 모든 마우스는 키보드입니다.
Options −
A − 내가 유효한 결론 만
B − 결론 II 만 유효합니다.
C − I 또는 II 중 하나가 유효합니다.
D − 유효한 결론이 없음
E − I와 II 모두 유효
Answer − 옵션 D
Explanation − 두 진술 모두 특별하므로 명확한 결론은 유효하지 않습니다.
Sample − 3
Statements −
모든 학생들은 냉정합니다. 모든 학생들은 장난 꾸러기입니다.
Conclusions −
I. 모든 장난 꾸러기는 냉정하거나 그 반대입니다.
II. 일부 냉정한 사람들은 장난 꾸러기입니다.
III. 일반적으로 음란 한 것은 술에 취하지 않습니다.
IV. 범죄와 죄책감은 함께갑니다.
Options −
A − 내가 유효한 결론 만
B − 결론 II 만 유효합니다.
C − I 또는 II 중 하나가 유효합니다.
D − I 또는 II 중 어느 것도 유효하지 않습니다.
E − I와 II 모두 유효
Answer − 옵션 B
Explanation− 성명서에 '학생'이라는 중간 용어가 두 번 분포되어 있기 때문에 결론이 광범위 할 수 없습니다. 따라서 '어떤 냉정한 사람은 장난 꾸러기'가 타당하다. 따라서 II는 사실입니다.