ภูมิภาคของการบรรจบกัน (ROC)

การแปรผันของช่วงของσซึ่งการแปลงลาปลาซมาบรรจบกันเรียกว่าพื้นที่ของคอนเวอร์เจนซ์

คุณสมบัติของ ROC ของ Laplace Transform

• ROC มีเส้นสตริปขนานกับแกนjωในระนาบ

  

• ถ้า x (t) เป็นอินทิกรัลอย่างแน่นอนและมีระยะเวลา จำกัด ดังนั้น ROC คือ s-plane ทั้งหมด

• ถ้า x (t) เป็นลำดับด้านขวาแล้ว ROC: Re {s}> σ o

• ถ้า x (t) เป็นลำดับด้านซ้ายแล้ว ROC: Re {s} <σ o

• ถ้า x (t) เป็นลำดับสองด้านดังนั้น ROC คือการรวมสองภูมิภาค

ROC สามารถอธิบายได้โดยใช้ตัวอย่างที่ระบุด้านล่าง:

Example 1: Find the Laplace transform and ROC of $x(t) = e-^{at}u(t)$

$ LT [x (t)] = LT [e - ^ {at} u (t)] = {1 \ over S + a} $

$ Re {} \ gt -a $

$ ROC: Re {s} \ gt> -a $

Example 2: Find the Laplace transform and ROC of $x(t) = e^{at}u(-t)$

$ LT [x (t)] = LT [e ^ {at} u (t)] = {1 \ over Sa} $

$ Re {s} <a $

$ ROC: Re {s} <a $

Example 3: Find the Laplace transform and ROC of $x(t) = e^{-at}u(t)+e^{at}u(-t)$

$ LT [x (t)] = LT [e ^ {- at} u (t) + e ^ {at} u (-t)] = {1 \ over S + a} + {1 \ over Sa} $

สำหรับ $ {1 \ over S + a} Re \ {s \} \ gt -a $

สำหรับ $ {1 \ over Sa} Re \ {s \} \ lt a $

การอ้างอิงถึงแผนภาพด้านบนขอบเขตการรวมอยู่ระหว่าง –a ถึง a ดังนั้น

$ ROC: -a <Re {s} <a $

เวรกรรมและความมั่นคง

• เพื่อให้ระบบมีความเป็นเหตุเป็นผลเสาทั้งหมดของฟังก์ชันการถ่ายโอนต้องอยู่ทางขวาครึ่งหนึ่งของระนาบ

  

• ระบบกล่าวว่าจะเสถียรเมื่อเสาทั้งหมดของฟังก์ชันการถ่ายโอนวางอยู่ทางด้านซ้ายของระนาบ s

  

• ระบบได้รับการกล่าวว่าไม่เสถียรเมื่ออย่างน้อยหนึ่งขั้วของฟังก์ชันการถ่ายโอนถูกเลื่อนไปทางครึ่งขวาของระนาบ

  

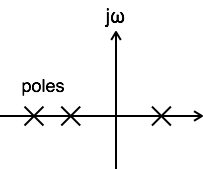
• ระบบได้รับการกล่าวว่ามีความเสถียรเล็กน้อยเมื่ออย่างน้อยหนึ่งขั้วของฟังก์ชันการถ่ายโอนอยู่บนแกน j s ของ s-plane

  

ROC ของฟังก์ชันพื้นฐาน

ฉ (t)	F (s)	ร็อค
$ u (t) $	$$ {1 \ over s} $$	ROC: Re {s}> 0
$ t \ u (t) $	$$ {1 \ over s ^ 2} $$	ROC: Re {s}> 0
$ t ^ n \, u (t) $	$$ {น! \ กว่า s ^ {n + 1}} $$	ROC: Re {s}> 0
$ e ^ {at} \, u (t) $	$$ {1 \ over sa} $$	ROC: Re {s}> ก
$ e ^ {- ที่} \, u (t) $	$$ {1 \ over s + a} $$	ROC: Re {s}> -a
$ e ^ {at} \, u (t) $	$$ - {1 \ over sa} $$	ROC: Re {s} <a
$ e ^ {- ที่} \, u (-t) $	$$ - {1 \ over s + a} $$	ROC: Re {s} <-a
$ t \, e ^ {at} \, u (t) $	$$ {1 \ over (sa) ^ 2} $$	ROC: Re {s}> ก
$ t ^ {n} e ^ {at} \, u (t) $	$$ {น! \ over (sa) ^ {n + 1}} $$	ROC: Re {s}> ก
$ t \, e ^ {- at} \, u (t) $	$$ {1 \ over (s + a) ^ 2} $$	ROC: Re {s}> -a
$ t ^ n \, e ^ {- at} \, u (t) $	$$ {น! \ over (s + a) ^ {n + 1}} $$	ROC: Re {s}> -a
$ t \, e ^ {at} \, u (-t) $	$$ - {1 \ over (sa) ^ 2} $$	ROC: Re {s} <a
$ t ^ n \, e ^ {at} \, u (-t) $	$$ - {n! \ over (sa) ^ {n + 1}} $$	ROC: Re {s} <a
$ t \, e ^ {- at} \, u (-t) $	$$ - {1 \ over (s + a) ^ 2} $$	ROC: Re {s} <-a
$ t ^ n \, e ^ {- at} \, u (-t) $	$$ - {n! \ over (s + a) ^ {n + 1}} $$	ROC: Re {s} <-a
$ e ^ {- at} \ cos \, bt $	$$ {s + a \ over (s + a) ^ 2 + b ^ 2} $$
$ e ^ {- at} \ sin \, bt $	$$ {b \ over (s + a) ^ 2 + b ^ 2} $$