Z-Transforms คุณสมบัติ

Z-Transform มีคุณสมบัติดังต่อไปนี้:

คุณสมบัติเชิงเส้น

ถ้า $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

และ $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $

จากนั้นคุณสมบัติเชิงเส้นระบุว่า

$ a \, x (n) + b \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} a \, X (Z) + b \, Y (Z) $

เวลาขยับทรัพย์สิน

ถ้า $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

จากนั้นคุณสมบัติการเปลี่ยนเวลาระบุว่า

$ x (nm) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} z ^ {- m} X (Z) $

การคูณด้วยคุณสมบัติของลำดับเอ็กซ์โปเนนเชียล

ถ้า $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

จากนั้นการคูณด้วยคุณสมบัติลำดับเลขชี้กำลังระบุว่า

$ a ^ n \,. x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z / a) $

คุณสมบัติการกลับรายการเวลา

ถ้า $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

จากนั้นคุณสมบัติการกลับตัวของเวลาระบุว่า

$ x (-n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (1 / Z) $

ความแตกต่างใน Z-Domain หรือการคูณด้วย n คุณสมบัติ

ถ้า $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

จากนั้นการคูณด้วย n หรือความแตกต่างในคุณสมบัติ z-domain ระบุว่า

$ n ^ kx (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} [-1] ^ kz ^ k {d ^ k X (Z) \ มากกว่า dZ ^ K} $

คุณสมบัติ Convolution

ถ้า $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

และ $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $

จากนั้นคุณสมบัติการแปลงสภาพระบุว่า

$ x (n) * y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z) $

คุณสมบัติสหสัมพันธ์

ถ้า $ \, x (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) $

และ $ \, y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} Y (Z) $

จากนั้นคุณสมบัติสหสัมพันธ์ระบุว่า

$ x (n) \ otimes y (n) \ stackrel {\ mathrm {ZT}} {\ longleftrightarrow} X (Z) .Y (Z ^ {- 1}) $

ค่าเริ่มต้นและทฤษฎีบทมูลค่าสุดท้าย

ค่าเริ่มต้นและทฤษฎีบทค่าสุดท้ายของการแปลง z ถูกกำหนดไว้สำหรับสัญญาณเชิงสาเหตุ

ทฤษฎีบทค่าเริ่มต้น

สำหรับสัญญาณเชิงสาเหตุ x (n) ทฤษฎีบทค่าเริ่มต้นระบุว่า

$ x (0) = \ lim_ {z \ to \ infty} ⁡X (z) $

ใช้เพื่อค้นหาค่าเริ่มต้นของสัญญาณโดยไม่ต้องใช้การแปลง z แบบผกผัน

ทฤษฎีบทมูลค่าสุดท้าย

สำหรับสัญญาณเชิงสาเหตุ x (n) ทฤษฎีบทค่าสุดท้ายระบุว่า

$ x (\ infty) = \ lim_ {z \ ถึง 1} [z-1] ⁡X (z) $

ใช้เพื่อค้นหาค่าสุดท้ายของสัญญาณโดยไม่ต้องใช้การแปลง z แบบผกผัน

Region of Convergence (ROC) ของ Z-Transform

ช่วงของการแปรผันของ z ที่การแปลงการแปลง z เรียกว่าขอบเขตการบรรจบกันของการแปลง z

คุณสมบัติของ ROC ของ Z-Transforms

ROC ของ z-transform จะแสดงด้วยวงกลมในระนาบ z
ROC ไม่มีเสาใด ๆ
ถ้า x (n) เป็นลำดับสาเหตุของระยะเวลา จำกัด หรือลำดับด้านขวา ROC จะเป็นระนาบ z ทั้งหมดยกเว้นที่ z = 0
ถ้า x (n) เป็นลำดับการต่อต้านสาเหตุระยะเวลา จำกัด หรือลำดับด้านซ้ายดังนั้น ROC จะเป็นระนาบ z ทั้งหมดยกเว้นที่ z = ∞
ถ้า x (n) เป็นลำดับสาเหตุของระยะเวลาที่ไม่สิ้นสุด ROC จะอยู่ด้านนอกของวงกลมที่มีรัศมี aie | z | > ก.
ถ้า x (n) เป็นลำดับการต่อต้านสาเหตุที่มีระยะเวลาไม่สิ้นสุด ROC จะอยู่ภายในวงกลมที่มีรัศมี aie | z | <a.
ถ้า x (n) เป็นระยะเวลา จำกัด สองลำดับด้านดังนั้น ROC จะเป็นระนาบ z ทั้งหมดยกเว้นที่ z = 0 & z = ∞

แนวคิดของ ROC สามารถอธิบายได้จากตัวอย่างต่อไปนี้:

Example 1: ค้นหา z-transform และ ROC ของ $ a ^ nu [n] + a ^ {-} nu [-n-1] $

$ ZT [a ^ nu [n]] + ZT [a ^ {- n} u [-n-1]] = {Z \ over Za} + {Z \ over Z {-1 \ over a}} $

$$ ROC: | z | \ gt a \ quad \ quad ROC: | z | \ lt {1 \ over a} $$

พล็อตของ ROC มีสองเงื่อนไขคือ a> 1 และ a <1 เนื่องจากคุณไม่ทราบก.

ในกรณีนี้ไม่มี ROC รวมกัน

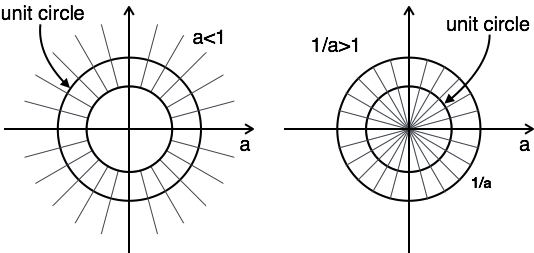
ที่นี่การรวมกันของ ROC มาจาก $ a \ lt | z | \ lt {1 \ over a} $

ดังนั้นสำหรับปัญหานี้การแปลง z จึงเป็นไปได้เมื่อ a <1

เวรกรรมและความมั่นคง

เงื่อนไขเชิงสาเหตุสำหรับระบบ LTI เวลาไม่ต่อเนื่องมีดังนี้:

ระบบ LTI เวลาไม่ต่อเนื่องเป็นสาเหตุเมื่อ

ROC อยู่นอกขั้วนอกสุด
ในฟังก์ชันการถ่ายโอน H [Z] ลำดับของตัวเศษจะไม่สามารถขูดได้มากกว่าลำดับของตัวส่วน

สภาพความเสถียรสำหรับระบบ LTI เวลาไม่ต่อเนื่อง

ระบบ LTI เวลาไม่ต่อเนื่องจะเสถียรเมื่อ

ฟังก์ชันระบบ H [Z] รวมวงกลมหน่วย | z | = 1
เสาทั้งหมดของฟังก์ชันการถ่ายโอนอยู่ในวงกลมหน่วย | z | = 1

Z-Transform ของสัญญาณพื้นฐาน

x (t)	X [Z]
$ \ delta $	1
$ u (n) $	$ {Z \ มากกว่า Z-1} $
$ u (-n-1) $	$ - {Z \ มากกว่า Z-1} $
$ \ delta (nm) $	$ z ^ {- m} $
$ a ^ nu [n] $	$ {Z \ over Za} $
$ a ^ nu [-n-1] $	$ - {Z \ over Za} $
$ n \, a ^ nu [n] $	$ {aZ \ over \| Za \| ^ 2} $
$ n \, a ^ nu [-n-1] $	$ - {aZ \ over \| Za \| ^ 2} $
$ a ^ n \ cos \ omega nu [n] $	$ {Z ^ 2-aZ \ cos \ omega \ กว่า Z ^ 2-2aZ \ cos \ omega + a ^ 2} $
$ a ^ n \ sin \ omega nu [n] $	$ {aZ \ sin \ omega \ over Z ^ 2 -2aZ \ cos \ omega + a ^ 2} $