Sayısal Aritmetik Devreler

Bu bölümde İkili toplayıcı ve İkili çıkarıcı gibi temel aritmetik devreleri tartışalım. Bu devreler 0 ve 1 ikili değerleri ile çalıştırılabilir.

İkili Toplayıcı

En temel aritmetik işlem toplamadır. İki ikili sayının toplamasını gerçekleştiren devre olarak bilinir.Binary adder. İlk olarak, iki bitin toplamasını gerçekleştiren bir toplayıcı uygulayalım.

Yarım Toplayıcı

Yarım toplayıcı, A ve B'nin iki ikili sayısının eklenmesini gerçekleştiren kombinasyonel bir devredir. single bit. Sum, S & Carry, C olmak üzere iki çıktı üretir

Truth table Yarım toplayıcı aşağıda gösterilmiştir.

Girişler		çıktılar
Bir	B	C	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

İki bitin toplamasını yaptığımızda, sonuçtaki toplam, ondalık olarak 0 ile 2 arasında değişen değerlere sahip olabilir. 0 ve 1 ondalık basamaklarını ikili olarak tek bit ile temsil edebiliriz. Ama ondalık basamak 2'yi ikili olarak tek bit ile temsil edemeyiz. Dolayısıyla, onu ikili olarak temsil etmek için iki bit gerekir.

Let, sum, S, En az anlamlı bit ve taşıma, C sonuçtaki toplamın En anlamlı biti olsun. Girişlerin ilk üç kombinasyonu için, taşıma, C sıfırdır ve S'nin değeri sıfır veya bir olacaktır.number of onesgirişlerde mevcut. Ancak, girdilerin son kombinasyonu için, taşıma, C birdir ve toplam, S sıfırdır, çünkü sonuçtaki toplam iki olur.

Doğruluk tablosundan, doğrudan Boolean functions her çıktı için

$$ S = A \ oplus B $$

$ C = AB $

Yukarıdaki işlevleri 2-girişli Ex-OR kapısı ve 2-girişli AND geçidi ile uygulayabiliriz. circuit diagram Yarım toplayıcı aşağıdaki şekilde gösterilmiştir.

Yukarıdaki devrede, iki girişli bir Ex-OR geçidi ve iki girişli AND geçidi sırasıyla toplam, S ve taşıma, C üretir. Bu nedenle Half-toplayıcı, iki bitin eklenmesini gerçekleştirir.

Tam Toplayıcı

Tam toplayıcı, birleşimsel bir devredir ve addition of three bitsA, B ve C _girişi . Burada, A ve B iki paralel anlamlı bittir ve C _in , önceki aşamadan üretilen taşıma bitidir. Bu Tam toplayıcı ayrıca Half toplayıcıya benzer iki çıktı toplamı, S & Carry, C _out üretir .

Truth table Tam toplayıcı aşağıda gösterilmiştir.

Girişler			çıktılar
A	B	Cin	Cout	S
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

Üç bitin toplamasını yaptığımızda, ortaya çıkan toplam, ondalık olarak 0 ile 3 arasında değişen değerlere sahip olabilir. 0 ve 1 ondalık basamaklarını ikili olarak tek bit ile temsil edebiliriz. Ancak, 2 ve 3 ondalık basamaklarını ikili olarak tek bit ile temsil edemeyiz. Dolayısıyla, bu iki ondalık basamağı ikili olarak temsil etmek için iki bit gerekir.

Let, sum, S, En az anlamlı bit ve Carry, C _out , sonuçtaki toplamın En önemli biti. Doğruluk tablosundaki tüm girdi kombinasyonları için çıktıların değerlerini doldurmak kolaydır. Sadece saynumber of onesgirişlerde bulunur ve çıkışlara eşdeğer ikili sayıyı yazın. C _in sıfıra eşitse, Tam toplayıcı doğruluk tablosu, Yarım toplayıcı doğruluk tablosu ile aynıdır.

Aşağıdakileri alacağız Boolean functions basitleştirmeden sonra her çıktı için.

$$ S = A \ oplus B \ oplus C_ {in} $$

$ c_ {çıkış} = AB + \ sol (A \ oplus B \ sağ) c_ {giriş} $

Toplam, S, girişlerde tek sayı bulunanlar olduğunda bire eşittir. Ex-OR geçidinin tek bir fonksiyon olan bir çıktı ürettiğini biliyoruz. Dolayısıyla, S toplamı üretmek için iki 2 girişli Ex-OR geçidi veya bir 3-girişli Ex-OR geçidi kullanabiliriz. İki 2-girişli AND geçidi ve bir OR geçidi kullanarak carry, C _out uygulayabiliriz . circuit diagram Aşağıdaki şekilde tam toplayıcı gösterilmektedir.

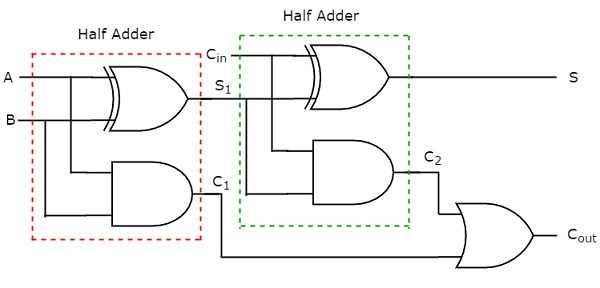
Bu toplayıcıya Full adderçünkü bir Tam toplayıcı uygulamak için iki Yarım toplayıcıya ve bir OR geçidine ihtiyacımız var. C _girişi sıfırsa, Tam toplayıcı Yarı toplayıcı olur. Yukarıdaki devre şemasından veya Full toplayıcının çıkışlarının Boole fonksiyonlarından kolayca doğrulayabiliriz.

4-bit İkili Toplayıcı

4 bitlik ikili toplayıcı, addition of two 4-bit numbers. 4 bitlik ikili sayılar, $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ ve $ B = B_ {3} B_ {2} B_ {1} B_ {0} $ olsun. 4 bitlik ikili toplayıcıyı aşağıdaki iki yoldan biriyle uygulayabiliriz.

• En az iki önemli bitin eklenmesi için bir Yarım toplayıcı ve üç yüksek anlamlı bitin eklenmesi için üç Tam toplayıcı kullanın.

• Tekdüzelik için dört Tam toplayıcı kullanın. Başlangıçta C _girişi sıfır olduğundan, en az anlamlı bitleri eklemek için kullanılan Tam toplayıcı Yarı toplayıcı olur.

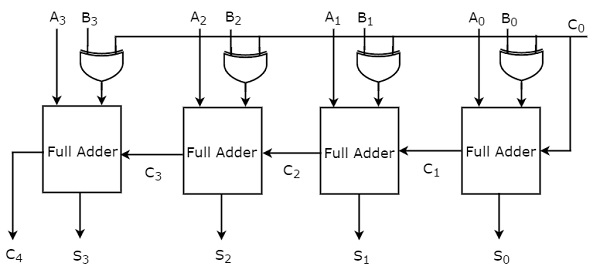
Şimdilik ikinci yaklaşımı düşündük. block diagram 4 bitlik ikili toplayıcı aşağıdaki şekilde gösterilmektedir.

Burada, 4 Tam toplayıcı basamaklıdır. Her Tam toplayıcı, iki paralel giriş A ve B'nin ilgili bitlerini alır. Bir Tam toplayıcının taşıma çıkışı, sonraki yüksek dereceli Tam toplayıcının taşıma girişi olacaktır. Bu 4 bitlik ikili toplayıcı, en fazla 5 bitlik sonuç toplamını üretir. Yani, son aşamada gerçekleştirilecek Tam toplayıcı MSB olacaktır.

Bu şekilde, herhangi bir yüksek dereceden ikili toplayıcıyı sadece gerekli Tam toplayıcı sayısını basamaklayarak uygulayabiliriz. Bu ikili toplayıcı aynı zamandaripple carry (binary) adder çünkü taşıma, bir aşamadan bir sonraki aşamaya yayılır (dalgalanmalar).

İkili Çıkarıcı

İki ikili sayının çıkarılmasını gerçekleştiren devre olarak bilinir Binary subtractor. Binary çıkarıcıyı aşağıdaki iki yöntemle uygulayabiliriz.

• Cascade Full çıkarıcılar
• 2'nin tamamlama yöntemi

İlk yöntemde, 'n' Full çıkarıcıları basamaklayarak bir n-bit ikili çıkarıcı elde edeceğiz. Bu nedenle, ilk önce Yarım çıkarıcı ve Tam çıkarıcıyı Yarım toplayıcı ve Tam toplayıcıya benzer şekilde uygulayabilirsiniz. Ardından, 'n' Full çıkarıcıları basamaklayarak n-bit ikili çıkarıcı uygulayabilirsiniz. Böylece, iki ikili sayının ikili toplama ve çıkarma işlemi için iki ayrı devremiz olacak.

İkinci yöntemde, sadece ikinci girişte bazı değişiklikler yaparak iki ikili sayıyı çıkarmak için aynı ikili toplayıcıyı kullanabiliriz. Böylece, dahili olarak ikili toplama işlemi gerçekleşir, ancak çıktı, sonuçta çıkan çıkarmadır.

A ve B ikili sayısının çıkarılmasının şu şekilde yazılabileceğini biliyoruz:

$$ AB = A + \ left ({2} 's \: iltifat \: / \: B \ sağ) $$

$ \ Rightarrow AB = A + \ left ({1} 's \: iltifat \: / \: B \ sağ) + 1 $

4-bit İkili Çıkarıcı

4 bitlik ikili çıkarıcı, subtraction of two 4-bit numbers. 4 bitlik ikili sayıları, $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ ve $ B = B_ {3} B_ {2} B_ {1} B_ {0} $ olsun. Dahili olarak, 4 bitlik İkili çıkarıcının çalışması 4 bitlik İkili toplayıcıya benzer. İkili sayı A'nın normal bitleri, ikili sayı B'nin tamamlanmış bitleri ve ilk taşıma (ödünç alma), bir olarak C _in 4-bit İkili toplayıcıya uygulanırsa, 4-bit İkili çıkarıcı olur. block diagram 4 bitlik ikili çıkarıcı aşağıdaki şekilde gösterilmiştir.

Bu 4 bitlik ikili çıkarıcı, en fazla 5 bit olan bir çıktı üretir. İkili sayı A, İkili sayı B'den büyükse, çıktının MSB'si sıfırdır ve kalan bitler AB'nin büyüklüğünü tutar. İkili sayı A, İkili sayı B'den küçükse, çıktının MSB'si birdir. Öyleyse, AB'nin büyüklüğünü elde etmek için 2'nin çıktı tamamlayıcısını alın.

Bu şekilde, sadece gerekli sayıda Tam toplayıcıyı gerekli değişikliklerle kademelendirerek daha yüksek dereceden ikili çıkarıcıları uygulayabiliriz.

İkili Toplayıcı / Çıkarıcı

İki ikili sayının herhangi bir zamanda toplanmasını veya çıkarılmasını gerçekleştirmek için kullanılabilen devre, Binary Adder / subtractor. Hem İkili toplayıcı hem de İkili çıkarıcı, basamaklı bir dizi Tam toplayıcı içerir. İkili sayı A'nın giriş bitleri hem İkili toplayıcıda hem de İkili çıkarıcıda doğrudan uygulanır.

İkili toplayıcı ve İkili çıkarıcıda bulunan Tam toplayıcıların girişlerinde iki fark vardır.

• İkili sayı B'nin girdi bitleri, İkili toplayıcıdaki Tam toplayıcılara doğrudan uygulanırken, ikili sayı B'nin tamamlanan bitleri İkili çıkarıcıdaki Tam toplayıcılara uygulanır.

• İlk taşıma, C ₀ = 0, 4-bit İkili toplayıcıda uygulanırken, ilk taşıma (ödünç), C ₀ = 1, 4-bit İkili çıkarıcıda uygulanır.

Biliyoruz ki 2-input Ex-OR gatediğer girdi sıfır olduğunda ilk girdi ile aynı olan bir çıktı üretir. Benzer şekilde, diğer girdi bir olduğunda ilk girdinin tamamlayıcısı olan bir çıktı üretir.

Bu nedenle, B ikili sayısının giriş bitlerini 2-girişli Ex-OR kapılarına uygulayabiliriz. Tüm bu Ex-OR kapılarının diğer girişi C _0'dır . Bu nedenle, C ₀ değerine bağlı olarak , Ex-OR kapıları B ikili sayısının normal veya tamamlanmış bitlerini üretir.

4-bit İkili Toplayıcı / Çıkarıcı

4 bitlik ikili toplayıcı / çıkarıcı, ilk taşıma veya ödünç alma değerine ( ₀₎ dayalı olarak iki 4 bitlik sayının eklenmesini veya çıkarılmasını üretir . 4 bitlik ikili sayılar, $ A = A_ {3} A_ {2} A_ {1} A_ {0} $ ve $ B = B_ {3} B_ {2} B_ {1} B_ {0} $ olsun. 4-bit İkili toplayıcı / çıkarıcının çalışması, 4-bit İkili toplayıcı ve 4-bit İkili çıkarıcı ile benzerdir.

A ve B ikili sayılarının normal bitlerini ve ilk taşıma veya ödünç alma, C _0'ı harici olarak 4 bitlik bir ikili toplayıcıya uygulayın. block diagram 4 bitlik ikili toplayıcı / çıkarıcı aşağıdaki şekilde gösterilmiştir.

İlk taşıma, ₀ sıfırsa, o zaman her bir tam toplayıcı, A ve B ikili sayılarının normal bitlerini alır. Dolayısıyla, 4 bitlik ikili toplayıcı / çıkarıcı bir çıktı üretir;addition of two binary numbers A ve B.

İlk ödünç alma, _{0 bir} ise, o zaman her tam toplayıcı normal A ikili sayı bitlerini ve B ikili sayılarının tamamlanmış bitlerini alır. Dolayısıyla, 4 bitlik ikili toplayıcı / çıkarıcı bir çıktı üretir;subtraction of two binary numbers A ve B.

Bu nedenle, ek Ex-OR kapılarının yardımıyla, aynı devre iki ikili sayının hem toplanması hem de çıkarılması için kullanılabilir.