Dijital Devreler - Kodlayıcılar
Bir EncoderDekoderin ters çalışmasını gerçekleştiren kombinasyonel bir devredir. Maksimum 2 n giriş satırı ve 'n' çıkış satırına sahiptir. Girişe eşdeğer aktif olan bir ikili kod üretecektir. Bu nedenle, kodlayıcı 2 n giriş satırını 'n' bit ile kodlar . Kodlayıcılarda etkinleştirme sinyalinin temsil edilmesi isteğe bağlıdır.
4 ila 2 Kodlayıcı
4'ten 2'ye Enkoderin dört girişi Y 3 , Y 2 , Y 1 ve Y 0 ve iki çıkışı A 1 ve A 0 olsun . block diagram Aşağıdaki şekilde 4 ila 2 Kodlayıcı gösterilmektedir.

Herhangi bir zamanda, çıkışta ilgili ikili kodu elde etmek için bu 4 girişten sadece biri '1' olabilir. Truth table 4 ila 2 kodlayıcı aşağıda gösterilmiştir.
| Girişler | çıktılar | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
Hakikat tablosundan şunu yazabiliriz: Boolean functions her çıktı için
$$ A_ {1} = Y_ {3} + Y_ {2} $$
$$ A_ {0} = Y_ {3} + Y_ {1} $$
Yukarıdaki iki Boole işlevini iki giriş VEYA geçidi kullanarak gerçekleştirebiliriz. circuit diagram Aşağıdaki şekilde 4 ila 2 kodlayıcı gösterilmektedir.

Yukarıdaki devre şeması iki OR geçidi içerir. Bu OR kapıları, dört girişi iki bit ile kodlar
İkili Kodlayıcıya Sekizli
Sekizden ikiye Enkoder sekiz girişe, Y 7'den Y 0'a ve üç çıkış A 2 , A 1 ve A 0'a sahiptir . Sekizden ikiye kodlayıcı, 8 ila 3 kodlayıcıdan başka bir şey değildir. block diagram Sekizlikten ikiliye Enkoder aşağıdaki şekilde gösterilmiştir.
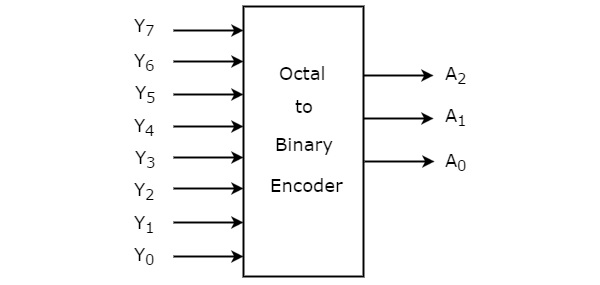
Herhangi bir zamanda, ilgili ikili kodu elde etmek için bu sekiz girişten yalnızca biri '1' olabilir. Truth table Sekizlikten ikiye kodlayıcı aşağıda gösterilmiştir.
| Girişler | çıktılar | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Hakikat tablosundan şunu yazabiliriz: Boolean functions her çıktı için
$$ A_ {2} = Y_ {7} + Y_ {6} + Y_ {5} + Y_ {4} $$
$$ A_ {1} = Y_ {7} + Y_ {6} + Y_ {3} + Y_ {2} $$
$$ A_ {0} = Y_ {7} + Y_ {5} + Y_ {3} + Y_ {1} $$
Yukarıdaki Boole işlevlerini dört giriş VEYA geçidi kullanarak gerçekleştirebiliriz. circuit diagram Sekizlikten ikiye enkoder aşağıdaki şekilde gösterilmektedir.

Yukarıdaki devre şeması, üç adet 4-girişli OR geçidi içerir. Bu VEYA kapıları, sekiz girişi üç bit ile kodlar.
Kodlayıcının Dezavantajları
Normal kodlayıcının dezavantajları aşağıdadır.
Kodlayıcının tüm çıktıları sıfıra eşit olduğunda bir belirsizlik vardır. Çünkü, yalnızca en az anlamlı girdi bir olduğunda veya tüm girdiler sıfır olduğunda, girdilere karşılık gelen kod olabilir.
Birden fazla giriş aktif Yüksek ise, o zaman kodlayıcı bir çıktı üretir ve bu doğru kod olmayabilir. İçinexampleY, her ikisi de eğer 3 ve Y, 6 olan '1', daha sonra kodlayıcı çıkışında 111 üretir. Bu, '1' olduğunda Y 3'e karşılık gelen eşdeğer kod veya '1' olduğunda Y 6'ya karşılık gelen eşdeğer kod değildir .
Dolayısıyla, bu zorlukların üstesinden gelmek için, her kodlayıcı girişine öncelikler atamalıyız. Ardından, kodlayıcının çıkışı, daha yüksek önceliğe sahip olan etkin Yüksek giriş (ler) e karşılık gelen (ikili) kod olacaktır. Bu kodlayıcıyapriority encoder.
Öncelikli Kodlayıcı
4 ila 2 öncelikli bir kodlayıcının dört girişi Y 3 , Y 2 , Y 1 ve Y 0 ve iki çıkışı A 1 ve A 0 vardır . Burada, Y 3 girdisi en yüksek önceliğe sahipken, Y 0 girdisi en düşük önceliğe sahiptir. Bu durumda, birden fazla giriş aynı anda '1' olsa bile, çıkış, sahip olduğu girişe karşılık gelen (ikili) kod olacaktır.higher priority.
Bir tane daha düşündük output, V çıkışlarda bulunan kodun geçerli olup olmadığını bilmek için.
Kodlayıcının en az bir girişi '1' ise, çıkışlarda bulunan kod geçerli bir koddur. Bu durumda çıktı, V 1'e eşit olacaktır.
Kodlayıcının tüm girişleri '0' ise, çıkışlarda bulunan kod geçerli değildir. Bu durumda çıktı, V, 0'a eşit olacaktır.
Truth table 4 ila 2 öncelikli kodlayıcı aşağıda gösterilmiştir.
| Girişler | çıktılar | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | V |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | x | 0 | 1 | 1 |
| 0 | 1 | x | x | 1 | 0 | 1 |
| 1 | x | x | x | 1 | 1 | 1 |
Kullanım 4 variable K-maps her çıktı için basitleştirilmiş ifadeler elde etmek için.
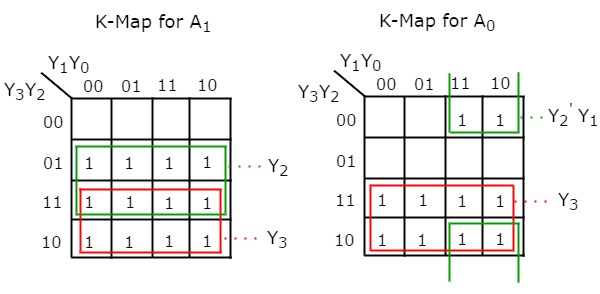
Basitleştirilmiş Boolean functions vardır
$$ A_ {1} = Y_ {3} + Y_ {2} $$
$ A_ {0} = Y_ {3} + {Y_ {2}} 'Y_ {1} $
Benzer şekilde, çıktının Boole işlevini, V olarak
$$ V = Y_ {3} + Y_ {2} + Y_ {1} + Y_ {0} $$
Mantık kapılarını kullanarak yukarıdaki Boole işlevlerini uygulayabiliriz. circuit diagram 4 ila 2 öncelikli kodlayıcı aşağıdaki şekilde gösterilmektedir.

Yukarıdaki devre şeması iki 2-girişli OR geçidi, bir 4-girişli OR geçidi, bir 2-girişli AND geçidi ve bir invertör içerir. Burada AND geçit ve inverter kombinasyonu, birden fazla giriş aynı anda '1'e eşit olsa bile çıkışlarda geçerli bir kod üretmek için kullanılır. Dolayısıyla, bu devre dört girişi iki bit ile kodlar.priority her girişe atanır.