Traitement numérique du signal - Guide rapide
Définition
Tout ce qui contient des informations peut être appelé comme signal. Elle peut également être définie comme une grandeur physique qui varie avec le temps, la température, la pression ou avec toute variable indépendante telle que le signal vocal ou le signal vidéo.
Le processus de fonctionnement dans lequel les caractéristiques d'un signal (amplitude, forme, phase, fréquence, etc.) subissent un changement est appelé traitement du signal.
Note- Tout signal indésirable interférant avec le signal principal est appelé bruit. Ainsi, le bruit est aussi un signal mais indésirable.
Selon leur représentation et leur traitement, les signaux peuvent être classés en diverses catégories dont les détails sont décrits ci-dessous.
Signaux de temps continus
Les signaux à temps continu sont définis le long d'un continuum de temps et sont donc représentés par une variable indépendante continue. Les signaux à temps continu sont souvent appelés signaux analogiques.
Ce type de signal montre une continuité à la fois en amplitude et en temps. Celles-ci auront des valeurs à chaque instant. Les fonctions sinus et cosinus sont le meilleur exemple de signal à temps continu.
Le signal montré ci-dessus est un exemple de signal de temps continu car nous pouvons obtenir la valeur du signal à chaque instant.
Signaux temporels discrets
Les signaux, qui sont définis à des instants discrets, sont appelés signaux discrets. Par conséquent, chaque variable indépendante a une valeur distincte. Ainsi, ils sont représentés comme une séquence de nombres.
Bien que les signaux vocaux et vidéo aient le privilège d'être représentés dans un format à la fois continu et discret; dans certaines circonstances, ils sont identiques. Les amplitudes présentent également des caractéristiques discrètes. Un exemple parfait de ceci est un signal numérique; dont l'amplitude et le temps sont tous deux discrets.
La figure ci-dessus représente la caractéristique d'amplitude discrète d'un signal discret sur une période de temps. Mathématiquement, ces types de signaux peuvent être formularisés comme;
$$x = \left \{ x\left [ n \right ] \right \},\quad -\infty < n< \infty$$Où, n est un entier.
C'est une séquence de nombres x, où le n ième nombre de la séquence est représenté par x [n].
Pour tester un système, on utilise généralement des signaux standard ou de base. Ces signaux sont les éléments de base de nombreux signaux complexes. Par conséquent, ils jouent un rôle très important dans l'étude des signaux et des systèmes.
Fonction d'impulsion d'unité ou de delta
Un signal, qui satisfait la condition, $\delta(t) = \lim_{\epsilon \to \infty} x(t)$est connu sous le nom de signal d'impulsion unitaire. Ce signal tend vers l'infini lorsque t = 0 et tend vers zéro lorsque t ≠ 0 de sorte que l'aire sous sa courbe soit toujours égale à un. La fonction delta a une amplitude nulle partout où excunit_impulse.jpgept à t = 0.

Propriétés du signal d'impulsion d'unité
- δ (t) est un signal pair.
- δ (t) est un exemple de signal ni énergie ni puissance (NENP).
- La zone du signal d'impulsion d'unité peut être écrite sous la forme; $$A = \int_{-\infty}^{\infty} \delta (t)dt = \int_{-\infty}^{\infty} \lim_{\epsilon \to 0} x(t) dt = \lim_{\epsilon \to 0} \int_{-\infty}^{\infty} [x(t)dt] = 1$$
- Le poids ou la force du signal peut s'écrire; $$y(t) = A\delta (t)$$
- La zone du signal d'impulsion pondéré peut être écrite comme - $$y (t) = \int_{-\infty}^{\infty} y (t)dt = \int_{-\infty}^{\infty} A\delta (t) = A[\int_{-\infty}^{\infty} \delta (t)dt ] = A = 1 = Wigthedimpulse$$
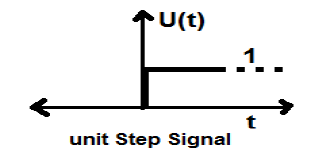
Signal d'étape de l'unité
Un signal qui satisfait les deux conditions suivantes -
- $U(t) = 1(when\quad t \geq 0 )and$
- $U(t) = 0 (when\quad t < 0 )$
est connu comme un signal de pas unitaire.
Il a la propriété de montrer la discontinuité à t = 0. Au point de discontinuité, la valeur du signal est donnée par la moyenne de la valeur du signal. Ce signal a été pris juste avant et après le point de discontinuité (selon les phénomènes de Gibb).
Si nous ajoutons un signal de pas à un autre signal de pas qui est mis à l'échelle du temps, le résultat sera l'unité. Il s'agit d'un signal de type puissance et la valeur de puissance est de 0,5. La valeur RMS (racine carrée moyenne) est de 0,707 et sa valeur moyenne est également de 0,5
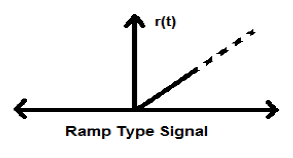
Signal de rampe
L'intégration du signal de pas entraîne un signal de rampe. Il est représenté par r (t). Le signal de rampe satisfait également la condition$r(t) = \int_{-\infty}^{t} U(t)dt = tU(t)$. Ce n'est ni un signal de type énergie ni puissance (NENP).
Signal parabolique
L'intégration du signal Ramp conduit au signal parabolique. Il est représenté par p (t). Le signal parabolique satisfait également la condition$p(t) = \int_{-\infty}^{t} r(t)dt = (t^{2}/2)U(t)$. Ce n'est ni un signal de type énergie ni puissance (NENP).
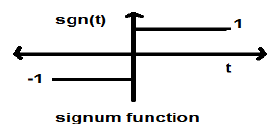
Fonction Signum
Cette fonction est représentée par
$$sgn(t) = \begin{cases}1 & for\quad t >0\\-1 & for\quad t<0\end{cases}$$C'est un signal de type puissance. Sa valeur de puissance et ses valeurs RMS (Root mean square) sont toutes deux égales à 1. La valeur moyenne de la fonction signum est zéro.
Fonction Sinc
C'est aussi une fonction du sinus et s'écrit -
$$SinC(t) = \frac{Sin\Pi t}{\Pi T} = Sa(\Pi t)$$Propriétés de la fonction Sinc
C'est un signal de type énergétique.
$Sinc(0) = \lim_{t \to 0}\frac{\sin \Pi t}{\Pi t} = 1$
$Sinc(\infty) = \lim_{t \to \infty}\frac{\sin \Pi \infty}{\Pi \infty} = 0$ (La plage de sinπ∞ varie entre -1 et +1 mais tout ce qui est divisé par l'infini est égal à zéro)
-
Si $ \sin c(t) = 0 => \sin \Pi t = 0$
$\Rightarrow \Pi t = n\Pi$
$\Rightarrow t = n (n \neq 0)$
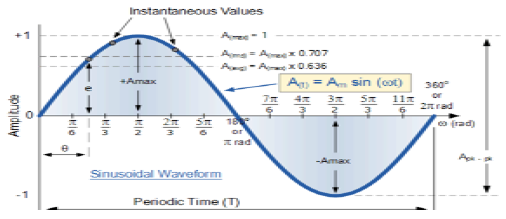
Signal sinusoïdal
Un signal, qui est de nature continue, est appelé signal continu. Le format général d'un signal sinusoïdal est
$$x(t) = A\sin (\omega t + \phi )$$Ici,
A = amplitude du signal
ω = Fréquence angulaire du signal (mesurée en radians)
φ = Angle de phase du signal (mesuré en radians)
La tendance de ce signal est de se répéter après une certaine période de temps, c'est pourquoi on l'appelle signal périodique. La période de temps du signal est donnée comme;
$$T = \frac{2\pi }{\omega }$$La vue schématique du signal sinusoïdal est illustrée ci-dessous.
Fonction rectangulaire
Un signal est dit de type fonction rectangulaire s'il satisfait à la condition suivante -
$$\pi(\frac{t}{\tau}) = \begin{cases}1, & for\quad t\leq \frac{\tau}{2}\\0, & Otherwise\end{cases}$$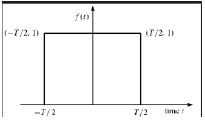
Étant symétrique par rapport à l'axe Y, ce signal est appelé signal pair.
Signal d'impulsion triangulaire
Tout signal satisfaisant à la condition suivante est appelé signal triangulaire.
$$\Delta(\frac{t}{\tau}) = \begin{cases}1-(\frac{2|t|}{\tau}) & for|t|<\frac{\tau}{2}\\0 & for|t|>\frac{\tau}{2}\end{cases}$$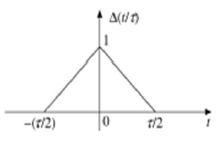
Ce signal est symétrique par rapport à l'axe Y. Par conséquent, il est également appelé signal pair.
Nous avons vu comment les signaux de base peuvent être représentés dans le domaine temporel continu. Voyons comment les signaux de base peuvent être représentés dans le domaine temporel discret.
Séquence d'impulsions de l'unité
Il est noté δ (n) dans le domaine temporel discret et peut être défini comme;
$$\delta(n)=\begin{cases}1, & for \quad n=0\\0, & Otherwise\end{cases}$$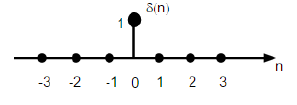
Signal d'étape de l'unité
Le signal de pas d'unité de temps discret est défini comme;
$$U(n)=\begin{cases}1, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$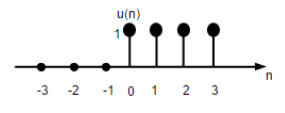
La figure ci-dessus montre la représentation graphique d'une fonction pas à pas discrète.
Fonction de rampe de l'unité
Une fonction de rampe d'unité discrète peut être définie comme -
$$r(n)=\begin{cases}n, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$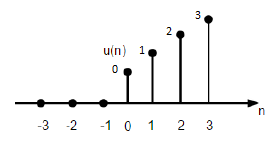
La figure ci-dessus montre la représentation graphique d'un signal de rampe discret.
Fonction parabolique
La fonction parabolique unitaire discrète est notée p (n) et peut être définie comme;
$$p(n) = \begin{cases}\frac{n^{2}}{2} ,& for \quad n\geq0\\0, & for \quad n<0\end{cases}$$En termes de fonction d'étape unitaire, il peut être écrit comme suit:
$$P(n) = \frac{n^{2}}{2}U(n)$$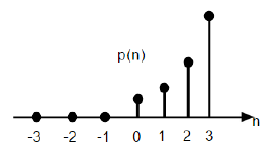
La figure ci-dessus montre la représentation graphique d'une séquence parabolique.
Signal sinusoïdal
Tous les signaux à temps continu sont périodiques. Les séquences sinusoïdales à temps discret peuvent être périodiques ou non. Ils dépendent de la valeur de ω. Pour qu'un signal temporel discret soit périodique, la fréquence angulaire ω doit être un multiple rationnel de 2π.
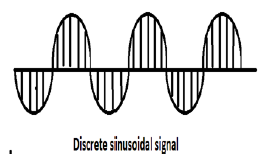
Un signal sinusoïdal discret est illustré dans la figure ci-dessus.
La forme discrète d'un signal sinusoïdal peut être représentée dans le format -
$$x(n) = A\sin(\omega n + \phi)$$Ici, A, ω et φ ont leur signification habituelle et n est l'entier. La période de temps du signal sinusoïdal discret est donnée par -
$$N =\frac{2\pi m}{\omega}$$Où, N et m sont des nombres entiers.
Les signaux de temps continu peuvent être classés selon différentes conditions ou opérations effectuées sur les signaux.
Signaux pairs et impairs
Signal uniforme
Un signal est dit égal s'il satisfait à la condition suivante;
$$x(-t) = x(t)$$L'inversion temporelle du signal n'implique ici aucun changement d'amplitude. Par exemple, considérons l'onde triangulaire ci-dessous.
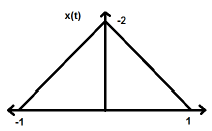
Le signal triangulaire est un signal pair. Depuis, il est symétrique par rapport à l'axe Y. Nous pouvons dire que c'est une image miroir autour de l'axe Y.
Considérez un autre signal comme indiqué dans la figure ci-dessous.
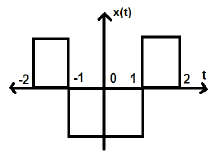
Nous pouvons voir que le signal ci-dessus est égal car il est symétrique par rapport à l'axe Y.
Signal étrange
Un signal est dit impair s'il satisfait à la condition suivante
$$x(-t) = -x(t)$$Ici, l'inversion du temps et le changement d'amplitude ont lieu simultanément.
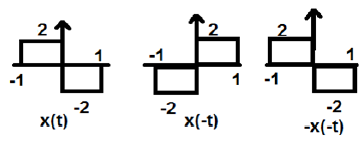
Dans la figure ci-dessus, nous pouvons voir un signal de pas x (t). Pour tester s'il s'agit d'un signal impair ou non, nous procédons d'abord à l'inversion du temps, c'est-à-dire x (-t) et le résultat est comme indiqué sur la figure. Ensuite, nous inversons l'amplitude du signal résultant, c'est-à-dire –x (-t) et nous obtenons le résultat comme indiqué sur la figure.
Si nous comparons la première et la troisième forme d'onde, nous pouvons voir qu'elles sont identiques, c'est-à-dire x (t) = -x (-t), ce qui satisfait nos critères. Par conséquent, le signal ci-dessus est un signal impair.
Quelques résultats importants liés aux signaux pairs et impairs sont donnés ci-dessous.
- Pair × Pair = Pair
- Impair × Impair = Pair
- Pair × Impair = Impair
- Paire ± Paire = Paire
- Impair ± Impair = Impair
- Pair ± Impair = Ni pair ni impair
Représentation de tout signal sous forme paire ou impaire
Certains signaux ne peuvent pas être directement classés en type pair ou impair. Ceux-ci sont représentés comme une combinaison de signaux pairs et impairs.
$$x(t)\rightarrow x_{e}(t)+x_{0}(t)$$Où x e (t) représente le signal pair et x o (t) représente le signal impair
$$x_{e}(t)=\frac{[x(t)+x(-t)]}{2}$$Et
$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$Exemple
Trouvez les parties paires et impaires du signal $x(n) = t+t^{2}+t^{3}$
Solution - En inversant x (n), on obtient
$$x(-n) = -t+t^{2}-t^{3}$$
Maintenant, selon la formule, la partie paire
$$x_{e}(t) = \frac{x(t)+x(-t)}{2}$$
$$= \frac{[(t+t^{2}+t^{3})+(-t+t^{2}-t^{3})]}{2}$$
$$= t^{2}$$
De même, selon la formule, la partie impaire est
$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$
$$= \frac{[(t+t^{2}+t^{3})-(-t+t^{2}-t^{3})]}{2}$$
$$= t+t^{3}$$
Signaux périodiques et non périodiques
Signaux périodiques
Le signal périodique se répète après un certain intervalle de temps. Nous pouvons le montrer sous forme d'équation comme -
$$x(t) = x(t)\pm nT$$Où, n = un entier (1,2,3 ……)
T = Période de temps fondamentale (FTP) ≠ 0 et ≠ ∞
La période de temps fondamentale (FTP) est la plus petite valeur de temps positive et fixe pour laquelle le signal est périodique.
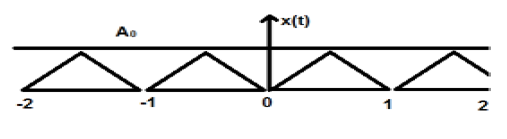
Un signal triangulaire est montré dans la figure ci-dessus d'amplitude A. Ici, le signal se répète toutes les 1 s. Par conséquent, on peut dire que le signal est périodique et que son FTP est de 1 s.
Signal non périodique
Simplement, on peut dire que les signaux, qui ne sont pas périodiques, sont de nature non périodique. Comme il est évident, ces signaux ne se répéteront pas après un intervalle de temps.
Les signaux non périodiques ne suivent pas un certain format; par conséquent, aucune équation mathématique particulière ne peut les décrire.
Signaux d'énergie et de puissance
Un signal est dit être un signal d'énergie, si et seulement si, l'énergie totale contenue est finie et non nulle (0 <E <∞). Par conséquent, pour tout signal de type d'énergie, le signal normalisé total est fini et non nul.
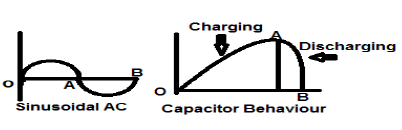
Un signal de courant alternatif sinusoïdal est un exemple parfait de signal de type Energy car il est en demi-cycle positif dans un cas, puis négatif dans le demi-cycle suivant. Par conséquent, sa puissance moyenne devient nulle.
Un condensateur sans perte est également un exemple parfait de signal de type énergie car lorsqu'il est connecté à une source, il se charge jusqu'à son niveau optimal et lorsque la source est supprimée, il dissipe cette quantité égale d'énergie à travers une charge et rend sa puissance moyenne à zéro.
Pour tout signal fini x (t), l'énergie peut être symbolisée par E et s'écrit;
$$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$La densité spectrale des signaux de type énergie donne la quantité d'énergie distribuée à différents niveaux de fréquence.
Signaux de type d'alimentation
Un signal est dit signal de type puissance, si et seulement si, la puissance moyenne normalisée est finie et non nulle, c'est-à-dire (0 <p <∞). Pour un signal de type puissance, la puissance moyenne normalisée est finie et non nulle. Presque tous les signaux périodiques sont des signaux de puissance et leur puissance moyenne est finie et non nulle.
Sous forme mathématique, la puissance d'un signal x (t) peut s'écrire;
$$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$Différence entre les signaux d'énergie et de puissance
Le tableau suivant résume les différences entre les signaux d'énergie et de puissance.
| Signal de puissance | Signal d'énergie |
|---|---|
| Les signaux périodiques pratiques sont des signaux de puissance. | Les signaux non périodiques sont des signaux d'énergie. |
| Ici, la puissance moyenne normalisée est finie et non nulle. | Ici, l'énergie normalisée totale est finie et non nulle. |
| Mathématiquement, $$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$ |
Mathématiquement, $$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$ |
| L'existence de ces signaux est infinie dans le temps. | Ces signaux existent pour une période de temps limitée. |
| L'énergie du signal de puissance est infinie sur un temps infini. | La puissance du signal d'énergie est nulle sur un temps infini. |
Exemples résolus
Example 1 - Trouver la puissance d'un signal $z(t) = 2\cos(3\Pi t+30^{o})+4\sin(3\Pi +30^{o})$
Solution- Les deux signaux ci-dessus sont orthogonaux l'un à l'autre car leurs termes de fréquence sont identiques l'un à l'autre également ils ont la même différence de phase. Ainsi, la puissance totale sera la somme des pouvoirs individuels.
Laisser $z(t) = x(t)+y(t)$
Où $x(t) = 2\cos (3\Pi t+30^{o})$ et $y(t) = 4\sin(3\Pi +30^{o})$
Le pouvoir de $x(t) = \frac{2^{2}}{2} = 2$
Le pouvoir de $y(t) = \frac{4^{2}}{2} = 8$
Par conséquent, $P(z) = p(x)+p(y) = 2+8 = 10$… Ans.
Example 2 - Tester si le signal donné $x(t) = t^{2}+j\sin t$ est conjugué ou pas?
Solution- Ici, la partie réelle étant t 2 est paire et la partie impaire (imaginaire) étant$\sin t$est impair. Ainsi, le signal ci-dessus est un signal conjugué.
Example 3 - Vérifiez si $X(t)= \sin \omega t$ est un signal impair ou un signal pair.
Solution - Donné $X(t) = \sin \omega t$
Par l'inversion du temps, nous obtiendrons $\sin (-\omega t)$
Mais nous savons que $\sin(-\phi) = -\sin \phi$.
Par conséquent,
$$\sin (-\omega t) = -\sin \omega t$$Ceci satisfait la condition pour qu'un signal soit impair. Par conséquent,$\sin \omega t$ est un signal étrange.
Tout comme les signaux à temps continu, les signaux à temps discret peuvent être classés en fonction des conditions ou des opérations sur les signaux.
Signaux pairs et impairs
Signal uniforme
Un signal est dit pair ou symétrique s'il satisfait à la condition suivante;
$$x(-n) = x(n)$$
Ici, nous pouvons voir que x (-1) = x (1), x (-2) = x (2) et x (-n) = x (n). Ainsi, c'est un signal pair.
Signal étrange
Un signal est dit impair s'il satisfait à la condition suivante;
$$x(-n) = -x(n)$$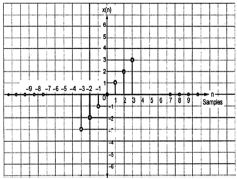
D'après la figure, nous pouvons voir que x (1) = -x (-1), x (2) = -x (2) et x (n) = -x (-n). Par conséquent, il s'agit d'un signal à la fois impair et antisymétrique.
Signaux périodiques et non périodiques
Un signal temporel discret est périodique si et seulement si, il satisfait la condition suivante -
$$x(n+N) = x(n)$$Ici, le signal x (n) se répète après N période. Ceci peut être mieux compris en considérant un signal cosinus -
$$x(n) = A \cos(2\pi f_{0}n+\theta)$$ $$x(n+N) = A\cos(2\pi f_{0}(n+N)+\theta) = A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$ $$= A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$Pour que le signal devienne périodique, la condition suivante doit être satisfaite;
$$x(n+N) = x(n)$$ $$\Rightarrow A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta) = A \cos(2\pi f_{0}n+\theta)$$c'est à dire $2\pi f_{0}N$ est un multiple entier de $2\pi$
$$2\pi f_{0}N = 2\pi K$$ $$\Rightarrow N = \frac{K}{f_{0}}$$Les fréquences des signaux sinusoïdaux discrets sont séparées par un multiple entier de $2\pi$.
Signaux d'énergie et de puissance
Signal d'énergie
L'énergie d'un signal temporel discret est notée E. Mathématiquement, elle peut s'écrire;
$$E = \displaystyle \sum\limits_{n=-\infty}^{+\infty}|x(n)|^2$$Si chaque valeur individuelle de $x(n)$sont au carré et ajoutés, nous obtenons le signal d'énergie. Ici$x(n)$ est le signal d'énergie et son énergie est finie dans le temps soit $ 0 <E <\ infty $
Signal de puissance
La puissance moyenne d'un signal discret est représentée par P. Mathématiquement, cela peut s'écrire;
$$P = \lim_{N \to \infty} \frac{1}{2N+1}\displaystyle\sum\limits_{n=-N}^{+N} |x(n)|^2$$Ici, la puissance est finie ie 0 <P <∞. Cependant, il existe certains signaux qui n'appartiennent ni à un signal de type énergie ni à un signal de type puissance.
Il existe d'autres signaux, qui sont le résultat d'une opération effectuée sur eux. Certains types courants de signaux sont décrits ci-dessous.
Signaux conjugués
Signaux, qui remplit la condition $x(t) = x*(-t)$ sont appelés signaux conjugués.
Laisser $x(t) = a(t)+jb(t)$... éqn. 1
Alors, $x(-t) = a(-t)+jb(-t)$
Et $x*(-t) = a(-t)-jb(-t)$... éqn. 2
Par condition, $x(t) = x*(-t)$
Si nous comparons les équations dérivées 1 et 2, nous pouvons voir que la partie réelle est paire, alors que la partie imaginaire est impaire. C'est la condition pour qu'un signal soit de type conjugué.
Signaux anti-symétriques conjugués
Signaux, qui satisfont la condition $x(t) = -x*(-t)$ sont appelés signaux antisymétriques conjugués
Laisser $x(t) = a(t)+jb(t)$... éqn. 1
Alors $x(-t) = a(-t)+jb(-t)$
Et $x*(-t) = a(-t)-jb(-t)$
$-x*(-t) = -a(-t)+jb(-t)$... éqn. 2
Par condition $x(t) = -x*(-t)$
Maintenant, comparez à nouveau les deux équations comme nous l'avons fait pour les signaux conjugués. Ici, nous verrons que la partie réelle est impaire et la partie imaginaire est paire. C'est la condition pour qu'un signal devienne de type anti-symétrique conjugué.
Exemple
Que le signal donné soit $x(t) = \sin t+jt^{2}$.
Ici, la vraie partie étant $\sin t$ est étrange et la partie imaginaire étant $t^2$est même. Ainsi, ce signal peut être classé comme signal antisymétrique conjugué.
Toute fonction peut être divisée en deux parties. Une partie étant la symétrie conjuguée et l'autre partie étant conjuguée anti-symétrique. Ainsi, tout signal x (t) peut être écrit comme
$$x(t) = xcs(t)+xcas(t)$$Où $xcs(t)$ est un signal symétrique conjugué et $xcas(t)$ est un signal anti symétrique conjugué
$$xcs(t) = \frac{[x(t)+x*(-t)]}{2}$$Et
$$xcas(t) = \frac{[x(t)-x*(-t)]}{2}$$Signaux symétriques demi-onde
Lorsqu'un signal satisfait la condition $cx(t) = -x(t\pm (\frac{T_{0}}{2}))$, il est appelé signal symétrique demi-onde. Ici, l'inversion d'amplitude et le décalage temporel du signal ont lieu à mi-temps. Pour un signal symétrique demi-onde, la valeur moyenne sera nulle mais ce n'est pas le cas lorsque la situation est inversée.
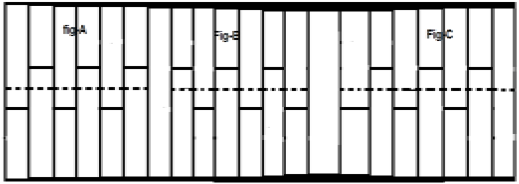
Considérons un signal x (t) comme le montre la figure A ci-dessus. La première étape consiste à décaler le signal dans le temps et à le faire$x[t-(\frac{T}{2})]$. Ainsi, le nouveau signal est modifié comme le montre la figure B. Ensuite, nous inversons l'amplitude du signal, c'est-à-dire le faisons$-x[t-(\frac{T}{2})]$ comme le montre la figure C. Puisque, ce signal se répète après un décalage à mi-temps et une inversion d'amplitude, il s'agit d'un signal symétrique demi-onde.
Signal orthogonal
Deux signaux x (t) et y (t) sont dits orthogonaux s'ils satisfont aux deux conditions suivantes.
Condition 1 - $\int_{-\infty}^{\infty}x(t)y(t) = 0$ [pour un signal non périodique]
Condition 2 - $\int x(t)y(t) = 0$ [Pour signal périodique]
Les signaux, qui contiennent des harmoniques impaires (3 ème , 5 ème , 7 ème ... etc.) Et ont des fréquences différentes, sont orthogonaux entre eux.
Dans les signaux de type trigonométrique, les fonctions sinus et les fonctions cosinus sont également orthogonales l'une à l'autre; à condition qu'ils aient la même fréquence et soient dans la même phase. De la même manière, les signaux DC (signaux de courant continu) et les signaux sinusoïdaux sont également orthogonaux l'un par rapport à l'autre. Si x (t) et y (t) sont deux signaux orthogonaux et$z(t) = x(t)+y(t)$ alors la puissance et l'énergie de z (t) peuvent s'écrire;
$$P(z) = p(x)+p(y)$$ $$E(z) = E(x)+E(y)$$Exemple
Analysez le signal: $z(t) = 3+4\sin(2\pi t+30^0)$
Ici, le signal comprend un signal CC (3) et une fonction sinus. Ainsi, par propriété, ce signal est un signal orthogonal et les deux sous-signaux qu'il contient sont orthogonaux l'un par rapport à l'autre.
Le décalage signifie le mouvement du signal, soit dans le domaine temporel (autour de l'axe Y) soit dans le domaine d'amplitude (autour de l'axe X). En conséquence, nous pouvons classer le décalage en deux catégories appelées décalage temporel et décalage d'amplitude, celles-ci sont ensuite discutées ci-dessous.
Changement de temps
Le décalage temporel signifie le décalage des signaux dans le domaine temporel. Mathématiquement, il peut être écrit comme
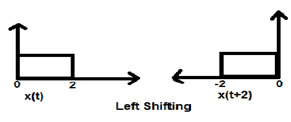
$$x(t) \rightarrow y(t+k)$$Cette valeur K peut être positive ou négative. Selon le signe de la valeur k, nous avons deux types de décalage nommés décalage à droite et décalage à gauche.
Cas 1 (K> 0)
Lorsque K est supérieur à zéro, le décalage du signal a lieu vers «gauche» dans le domaine temporel. Par conséquent, ce type de décalage est appelé décalage à gauche du signal.
Example
Cas 2 (K <0)
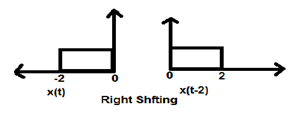
Lorsque K est inférieur à zéro, le décalage du signal a lieu vers la droite dans le domaine temporel. Par conséquent, ce type de décalage est connu sous le nom de décalage à droite.
Example
La figure ci-dessous montre le décalage vers la droite d'un signal de 2.
Décalage d'amplitude
Le décalage d'amplitude signifie le décalage du signal dans le domaine d'amplitude (autour de l'axe X). Mathématiquement, il peut être représenté par -
$$x(t) \rightarrow x(t)+K$$Cette valeur K peut être positive ou négative. En conséquence, nous avons deux types de décalage d'amplitude qui sont ensuite discutés ci-dessous.
Cas 1 (K> 0)
Lorsque K est supérieur à zéro, le décalage du signal a lieu vers le haut sur l'axe des x. Par conséquent, ce type de décalage est appelé déplacement vers le haut.
Example
Considérons un signal x (t) qui est donné comme;
$$x = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$Supposons que nous ayons pris K = + 1 pour que le nouveau signal puisse s'écrire -
$y(t) \rightarrow x(t)+1$ Ainsi, y (t) peut finalement s'écrire;
$$x(t) = \begin{cases}1, & t < 0\\2, & 0\leq t\leq 2\\ 1, & t>0\end{cases}$$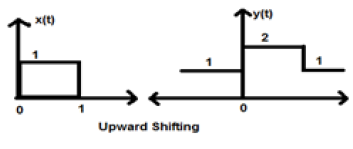
Cas 2 (K <0)
Lorsque K est inférieur à zéro, le décalage du signal a lieu vers le bas sur l'axe X. Par conséquent, on parle de décalage vers le bas du signal.
Example
Considérons un signal x (t) qui est donné comme;
$$x(t) = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$Supposons que nous ayons pris K = -1 pour que le nouveau signal puisse s'écrire;
$y(t)\rightarrow x(t)-1$ Ainsi, y (t) peut finalement s'écrire;
$$y(t) = \begin{cases}-1, & t < 0\\0, & 0\leq t\leq 2\\ -1, & t>0\end{cases}$$
Mise à l'échelle d'un signal signifie, une constante est multipliée par le temps ou l'amplitude du signal.
Mise à l'échelle du temps
Si une constante est multipliée sur l'axe des temps, on parle alors de mise à l'échelle du temps. Cela peut être représenté mathématiquement par;
$x(t) \rightarrow y(t) = x(\alpha t)$ ou $x(\frac{t}{\alpha})$; où α ≠ 0
Ainsi, l'axe des y étant le même, la grandeur de l'axe des x diminue ou augmente selon le signe de la constante (qu'elle soit positive ou négative). Par conséquent, la mise à l'échelle peut également être divisée en deux catégories, comme indiqué ci-dessous.
Compression du temps
Chaque fois que alpha est supérieur à zéro, l'amplitude du signal est divisée par alpha tandis que la valeur de l'axe Y reste la même. Ceci est connu sous le nom de compression temporelle.
Example
Considérons un signal x (t), qui est représenté comme dans la figure ci-dessous. Prenons la valeur de alpha égale à 2. Ainsi, y (t) sera x (2t), ce qui est illustré dans la figure donnée.

Clairement, nous pouvons voir à partir des figures ci-dessus que la grandeur de temps en axe y reste la même mais l'amplitude en axe x diminue de 4 à 2. Il s'agit donc d'un cas de compression temporelle.
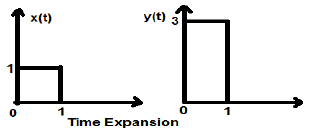
Expansion du temps
Lorsque le temps est divisé par l'alpha constant, l'amplitude de l'axe Y du signal est multipliée par alpha, en conservant l'amplitude de l'axe X telle qu'elle est. Par conséquent, cela s'appelle un signal de type à expansion temporelle.
Example
Considérons un signal carré x (t), de grandeur 1. Quand on le met à l'échelle temporelle par une constante 3, telle que $x(t) \rightarrow y(t) \rightarrow x(\frac{t}{3})$, puis l'amplitude du signal est modifiée par 3 fois, comme illustré dans la figure ci-dessous.
Mise à l'échelle de l'amplitude
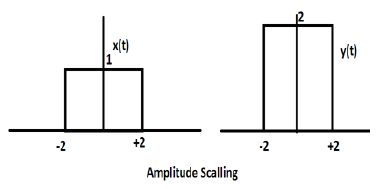
La multiplication d'une constante par l'amplitude du signal provoque une mise à l'échelle d'amplitude. Selon le signe de la constante, il peut s'agir d'une échelle d'amplitude ou d'une atténuation. Considérons un signal carré x (t) = Π (t / 4).
Supposons que nous définissions une autre fonction y (t) = 2 Π (t / 4). Dans ce cas, la valeur de l'axe des y sera doublée, en conservant la valeur de l'axe des temps telle quelle. Le est illustré dans la figure ci-dessous.
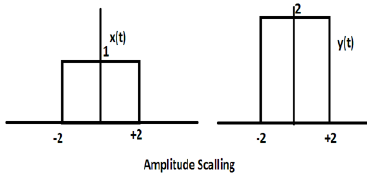
Considérons une autre fonction d'onde carrée définie comme z (t) où z (t) = 0,5 Π (t / 4). Ici, l'amplitude de la fonction z (t) sera la moitié de celle de x (t) c'est-à-dire que l'axe des temps reste le même, l'axe d'amplitude sera divisé par deux. Ceci est illustré par la figure ci-dessous.
Chaque fois que le temps d'un signal est multiplié par -1, le signal est inversé. Il produit son image miroir autour de l'axe Y ou X. C'est ce qu'on appelle l'inversion du signal.
L'inversion peut être classée en deux types en fonction de la condition que le temps ou l'amplitude du signal soit multiplié par -1.
Inversion du temps
Chaque fois que le temps du signal est multiplié par -1, on parle d'inversion temporelle du signal. Dans ce cas, le signal produit son image miroir autour de l'axe Y. Mathématiquement, cela peut être écrit comme;
$$x(t) \rightarrow y(t) \rightarrow x(-t)$$Cela peut être mieux compris par l'exemple suivant.

Dans l'exemple ci-dessus, nous pouvons clairement voir que le signal a été inversé autour de son axe Y. Il s'agit donc d'un type de mise à l'échelle temporelle également, mais ici la quantité de mise à l'échelle est toujours (-1).
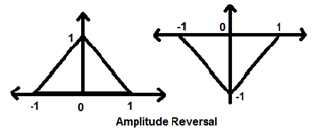
Inversion d'amplitude
Chaque fois que l'amplitude d'un signal est multipliée par -1, on parle alors d'inversion d'amplitude. Dans ce cas, le signal produit son image miroir autour de l'axe X. Mathématiquement, cela peut être écrit comme;
$$x(t)\rightarrow y(t)\rightarrow -x(t)$$Prenons l'exemple suivant. L'inversion d'amplitude est clairement visible.
Deux opérations très importantes effectuées sur les signaux sont la différenciation et l'intégration.
Différenciation
La différenciation de tout signal x (t) signifie une représentation de la pente de ce signal par rapport au temps. Mathématiquement, il est représenté par;
$$x(t)\rightarrow \frac{dx(t)}{dt}$$Dans le cas de la différenciation OPAMP, cette méthodologie est très utile. Nous pouvons facilement différencier un signal graphiquement plutôt que d'utiliser la formule. Cependant, la condition est que le signal doit être de type rectangulaire ou triangulaire, ce qui se produit dans la plupart des cas.
| Signal d'origine | Signal différencié |
|---|---|
| Rampe | Étape |
| Étape | Impulsion |
| Impulsion | 1 |
Le tableau ci-dessus illustre la condition du signal après avoir été différencié. Par exemple, un signal de rampe se convertit en un signal de pas après différenciation. De même, un signal de pas unitaire devient un signal d'impulsion.
Exemple
Que le signal qui nous est donné soit $x(t) = 4[r(t)-r(t-2)]$. Lorsque ce signal est tracé, il ressemblera à celui du côté gauche de la figure ci-dessous. Maintenant, notre objectif est de différencier le signal donné.
Pour commencer, nous allons commencer à différencier l'équation donnée. On sait que le signal de rampe après différenciation donne un signal de pas unitaire.
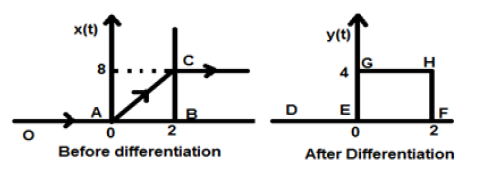
Ainsi, notre signal résultant y (t) peut s'écrire;
$y(t) = \frac{dx(t)}{dt}$
$= \frac{d4[r(t)-r(t-2)]}{dt}$
$= 4[u(t)-u(t-2)]$
Maintenant, ce signal est tracé finalement, ce qui est montré dans la partie droite de la figure ci-dessus.
L'intégration de tout signal signifie la sommation de ce signal dans un domaine temporel particulier pour obtenir un signal modifié. Mathématiquement, cela peut être représenté par -
$$x(t)\rightarrow y(t) = \int_{-\infty}^{t}x(t)dt$$Ici aussi, dans la plupart des cas, nous pouvons faire une intégration mathématique et trouver le signal résultant, mais une intégration directe en succession rapide est possible pour les signaux qui sont représentés graphiquement au format rectangulaire. A l'instar de la différenciation, ici aussi, nous référencerons un tableau pour obtenir le résultat rapidement.
| Signal d'origine | Signal intégré |
|---|---|
| 1 | impulsion |
| Impulsion | étape |
| Étape | Rampe |
Exemple
Considérons un signal $x(t) = u(t)-u(t-3)$. Il est illustré sur la figure 1 ci-dessous. De toute évidence, nous pouvons voir que c'est un signal de pas. Maintenant, nous allons l'intégrer. En se référant au tableau, nous savons que l'intégration du signal de pas donne un signal de rampe.
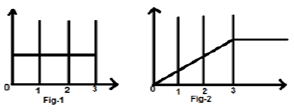
Cependant, nous le calculerons mathématiquement,
$y(t) = \int_{-\infty}^{t}x(t)dt$
$= \int_{-\infty}^{t}[u(t)-u(t-3)]dt$
$= \int_{-\infty}^{t}u(t)dt-\int_{-\infty}^{t}u(t-3)dt$
$= r(t)-r(t-3)$
La même chose est tracée comme indiqué sur la fig-2,
La convolution de deux signaux dans le domaine temporel équivaut à la multiplication de leur représentation dans le domaine fréquentiel. Mathématiquement, nous pouvons écrire la convolution de deux signaux comme
$$y(t) = x_{1}(t)*x_{2}(t)$$ $$= \int_{-\infty}^{\infty}x_{1}(p).x_{2}(t-p)dp$$Étapes de la convolution
- Prenez le signal x 1 (t) et mettez t = p ici pour qu'il soit x 1 (p).
- Prenez le signal x 2 (t) et effectuez l'étape 1 et faites-le x 2 (p).
- Faites le pliage du signal soit x 2 (-p).
- Effectuez le décalage temporel du signal ci-dessus x 2 [- (pt)]
- Faites ensuite la multiplication des deux signaux. c'est à dire$x_{1}(p).x_{2}[−(p−t)]$
Exemple
Faisons la convolution d'un signal de pas u (t) avec son propre type.
$y(t) = u(t)*u(t)$
$= \int_{-\infty}^{\infty}[u(p).u[-(p-t)]dp$
Maintenant, ce t peut être supérieur ou inférieur à zéro, comme le montrent les figures ci-dessous
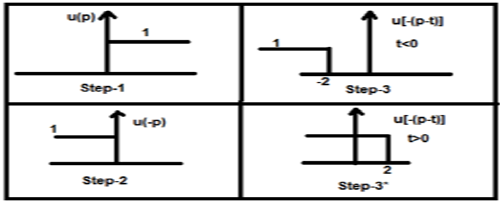
Donc, avec le cas ci-dessus, le résultat survient avec les possibilités suivantes
$y(t) = \begin{cases}0, & if\quad t<0\\\int_{0}^{t}1dt, & for\quad t>0\end{cases}$
$= \begin{cases}0, & if\quad t<0\\t, & t>0\end{cases} = r(t)$
Propriétés de la convolution
Commutatif
Il déclare que l'ordre de convolution n'a pas d'importance, ce qui peut être montré mathématiquement comme
$$x_{1}(t)*x_{2}(t) = x_{2}(t)*x_{1}(t)$$Associatif
Il déclare que l'ordre de convolution impliquant trois signaux peut être n'importe quoi. Mathématiquement, il peut être représenté par;
$$x_{1}(t)*[x_{2}(t)*x_{3}(t)] = [x_{1}(t)*x_{2}(t)]*x_{3}(t)$$Distributif
Deux signaux peuvent être ajoutés en premier, puis leur convolution peut être faite au troisième signal. Cela équivaut à la convolution de deux signaux individuellement avec le troisième signal et ajouté finalement. Mathématiquement, cela peut être écrit comme;
$$x_{1}(t)*[x_{2}(t)+x_{3}(t)] = [x_{1}(t)*x_{2}(t)+x_{1}(t)*x_{3}(t)]$$Surface
Si un signal est le résultat de la convolution de deux signaux, alors la zone du signal est la multiplication de ces signaux individuels. Mathématiquement, cela peut être écrit
Si $y(t) = x_{1}*x_{2}(t)$
Alors, Aire de y (t) = Aire de x 1 (t) X Aire de x 2 (t)
Mise à l'échelle
Si deux signaux sont mis à l'échelle à une constante inconnue «a» et qu'une convolution est effectuée, le signal résultant sera également convolué à la même constante «a» et sera divisé par cette quantité comme indiqué ci-dessous.
Si, $x_{1}(t)*x_{2}(t) = y(t)$
Ensuite, $x_{1}(at)*x_{2}(at) = \frac{y(at)}{a}, a \ne 0$
Retard
Supposons qu'un signal y (t) est le résultat de la convolution de deux signaux x1 (t) et x2 (t). Si les deux signaux sont retardés respectivement du temps t1 et t2, alors le signal résultant y (t) sera retardé de (t1 + t2). Mathématiquement, il peut s'écrire -
Si, $x_{1}(t)*x_{2}(t) = y(t)$
Ensuite, $x_{1}(t-t_{1})*x_{2}(t-t_{2}) = y[t-(t_{1}+t_{2})]$
Exemples résolus
Example 1 - Trouver la convolution des signaux u (t-1) et u (t-2).
Solution- Les signaux donnés sont u (t-1) et u (t-2). Leur convolution peut être effectuée comme indiqué ci-dessous -
$y(t) = u(t-1)*u(t-2)$
$y(t) = \int_{-\infty}^{+\infty}[u(t-1).u(t-2)]dt$
$= r(t-1)+r(t-2)$
$= r(t-3)$
Example 2 - Trouver la convolution de deux signaux donnée par
$x_{1}(n) = \lbrace 3,-2, 2\rbrace $
$x_{2}(n) = \begin{cases}2, & 0\leq n\leq 4\\0, & x > elsewhere\end{cases}$
Solution -
x 2 (n) peut être décodé comme$x_{2}(n) = \lbrace 2,2,2,2,2\rbrace Originalfirst$
x 1 (n) est donné précédemment$= \lbrace 3,-2,3\rbrace = 3-2Z^{-1}+2Z^{-2}$
De même, $x_{2}(z) = 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$
Signal résultant,
$X(Z) = X_{1}(Z)X_{2}(z)$
$= \lbrace 3-2Z^{-1}+2Z^{-2}\rbrace \times \lbrace 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}\rbrace$
$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+6Z^{-4}+6Z^{-5}$
En prenant la transformation Z inverse de ce qui précède, nous obtiendrons le signal résultant comme
$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$ Origine au premier
Example 3 - Déterminer la convolution des 2 signaux suivants -
$x(n) = \lbrace 2,1,0,1\rbrace$
$h(n) = \lbrace 1,2,3,1\rbrace$
Solution -
En prenant la transformation en Z des signaux, nous obtenons,
$x(z) = 2+2Z^{-1}+2Z^{-3}$
Et $h(n) = 1+2Z^{-1}+3Z^{-2}+Z^{-3}$
Maintenant, la convolution de deux signaux signifie la multiplication de leurs transformations Z
C'est $Y(Z) = X(Z) \times h(Z)$
$= \lbrace 2+2Z^{-1}+2Z^{-3}\rbrace \times \lbrace 1+2Z^{-1}+3Z^{-2}+Z^{-3}\rbrace$
$= \lbrace 2+5Z^{-1}+8Z^{-2}+6Z^{-3}+3Z^{-4}+3Z^{-5}+Z^{-6}\rbrace$
En prenant la transformation Z inverse, le signal résultant peut être écrit comme;
$y(n) = \lbrace 2,5,8,6,6,1 \rbrace Originalfirst$
Certains systèmes ont une rétroaction et d'autres pas. Celles qui n'ont pas de système de rétroaction, leur sortie dépend uniquement des valeurs actuelles de l'entrée. La valeur passée des données n'est pas présente à ce moment-là. Ces types de systèmes sont appelés systèmes statiques. Cela ne dépend pas non plus des valeurs futures.
Étant donné que ces systèmes n'ont aucun enregistrement antérieur, ils n'ont donc pas non plus de mémoire. Par conséquent, nous disons que tous les systèmes statiques sont des systèmes sans mémoire. Prenons un exemple pour mieux comprendre ce concept.
Exemple
Vérifions si les systèmes suivants sont des systèmes statiques ou non.
- $y(t) = x(t)+x(t-1)$
- $y(t) = x(2t)$
- $y(t) = x = \sin [x(t)]$
une) $y(t) = x(t)+x(t-1)$
Ici, x (t) est la valeur actuelle. Il n'a aucun rapport avec les valeurs passées de l'époque. Donc, c'est un système statique. Cependant, dans le cas de x (t-1), si nous mettons t = 0, cela se réduira à x (-1) qui est une valeur passée dépendante. Donc, ce n'est pas statique. Donc ici y (t) n'est pas un système statique.
b) $y(t) = x(2t)$
Si nous substituons t = 2, le résultat sera y (t) = x (4). Encore une fois, cela dépend de la valeur future. Donc, ce n'est pas non plus un système statique.
c) $y(t) = x = \sin [x(t)]$
Dans cette expression, nous avons affaire à une fonction sinusoïdale. La plage de la fonction sinus se situe entre -1 et +1. Ainsi, quelles que soient les valeurs que nous substituons à x (t), nous nous situerons entre -1 et +1. Par conséquent, nous pouvons dire qu'il ne dépend d'aucune valeur passée ou future. C'est donc un système statique.
À partir des exemples ci-dessus, nous pouvons tirer les conclusions suivantes -
- Tout système à décalage horaire n'est pas statique.
- Tout système ayant un décalage d'amplitude n'est pas non plus statique.
- Les cas d'intégration et de différenciation ne sont pas non plus statiques.
Si un système dépend de la valeur passée et future du signal à tout instant du temps, il est alors appelé système dynamique. Contrairement aux systèmes statiques, ce ne sont pas des systèmes sans mémoire. Ils stockent les valeurs passées et futures. Par conséquent, ils nécessitent de la mémoire. Comprenons mieux cette théorie à travers quelques exemples.
Exemples
Découvrez si les systèmes suivants sont dynamiques.
a) $y(t) = x(t+1)$
Dans ce cas, si nous mettons t = 1 dans l'équation, il sera converti en x (2), qui est une valeur dépendante future. Parce qu'ici, nous donnons la valeur 1, mais la valeur de x (2) est affichée. Comme il s'agit d'un futur signal dépendant, il s'agit clairement d'un système dynamique.
b) $y(t) = Real[x(t)]$
$$= \frac{[x(t)+x(t)^*]}{2}$$Dans ce cas, quelle que soit la valeur que nous mettrons, il affichera ce signal de valeur réelle de temps. Il n'a aucune dépendance des valeurs futures ou passées. Par conséquent, ce n'est pas un système dynamique mais plutôt un système statique.
c) $y(t) = Even[x(t)]$
$$= \frac{[x(t)+x(-t)]}{2}$$Ici, si nous substituons t = 1, un signal affiche x (1) et un autre affichera x (-1) qui est une valeur passée. De même, si nous mettons t = -1, un signal affichera x (-1) et un autre affichera x (1) qui est une valeur future. Par conséquent, il s'agit clairement d'un cas de système dynamique.
d) $y(t) = \cos [x(t)]$
Dans ce cas, comme le système est une fonction cosinus, il a un certain domaine de valeurs qui se situe entre -1 et +1. Par conséquent, quelles que soient les valeurs que nous mettrons, nous obtiendrons le résultat dans la limite spécifiée. C'est donc un système statique
À partir des exemples ci-dessus, nous pouvons tirer les conclusions suivantes -
- Tous les signaux de cas de décalage temporel sont des signaux dynamiques.
- En cas de mise à l'échelle temporelle également, tous les signaux sont des signaux dynamiques.
- Les signaux des cas d'intégration sont des signaux dynamiques.
Auparavant, nous avons vu que le système doit être indépendant des valeurs futures et passées pour devenir statique. Dans ce cas, la condition est presque la même avec peu de modifications. Ici, pour que le système soit causal, il ne doit être indépendant que des valeurs futures. Cela signifie que la dépendance passée ne posera aucun problème pour que le système devienne causal.
Les systèmes causaux sont des systèmes réalisables pratiquement ou physiquement. Prenons quelques exemples pour mieux comprendre cela.
Exemples
Considérons les signaux suivants.
a) $y(t) = x(t)$
Ici, le signal ne dépend que des valeurs actuelles de x. Par exemple, si nous substituons t = 3, le résultat ne s'affichera que pour cet instant. Par conséquent, comme il ne dépend pas de la valeur future, nous pouvons l'appeler un système causal.
b) $y(t) = x(t-1)$
Ici, le système dépend des valeurs passées. Par exemple, si nous substituons t = 3, l'expression se réduira à x (2), qui est une valeur passée par rapport à notre entrée. En aucun cas, cela ne dépend des valeurs futures. Par conséquent, ce système est également un système causal.
c) $y(t) = x(t)+x(t+1)$
Dans ce cas, le système comprend deux parties. La partie x (t), comme nous l'avons vu précédemment, ne dépend que des valeurs actuelles. Donc, il n'y a aucun problème avec cela. Cependant, si l'on prend le cas de x (t + 1), cela dépend clairement des valeurs futures car si on met t = 1, l'expression se réduira à x (2) qui est la valeur future. Par conséquent, ce n'est pas causal.
Un système non causal est juste opposé à celui d'un système causal. Si un système dépend des valeurs futures de l'entrée à tout instant du temps, alors le système est dit être un système non causal.
Exemples
Prenons quelques exemples et essayons de mieux comprendre cela.
a) $y(t) = x(t+1)$
Nous avons déjà discuté de ce système dans le système causal aussi. Pour toute entrée, cela réduira le système à sa valeur future. Par exemple, si nous mettons t = 2, cela se réduira à x (3), qui est une valeur future. Par conséquent, le système est non causal.
b) $y(t) = x(t)+x(t+2)$
Dans ce cas, x (t) est purement une fonction dépendante de la valeur actuelle. Nous avons déjà discuté que la fonction x (t + 2) est dépendante du futur car pour t = 3, elle donnera des valeurs pour x (5). Par conséquent, il est non causal.
c) $y(t) = x(t-1)+x(t)$
Dans ce système, cela dépend des valeurs présentes et passées de l'entrée donnée. Quelles que soient les valeurs que nous substituons, cela ne montrera jamais de dépendance future. De toute évidence, ce n'est pas un système non causal; c'est plutôt un système causal.
Un système anti-causal n'est qu'une version légèrement modifiée d'un système non causal. Le système dépend uniquement des valeurs futures de l'entrée. Il ne dépend ni des valeurs présentes ni des valeurs passées.
Exemples
Découvrez si les systèmes suivants sont anti-causaux.
a) $y(t) = x(t)+x(t-1)$
Le système a deux sous-fonctions. Une sous-fonction x (t + 1) dépend de la valeur future de l'entrée mais une autre sous-fonction x (t) ne dépend que du présent. Comme le système dépend de la valeur actuelle en plus de la valeur future, ce système n'est pas anti-causal.
b) $y(t) = x(t+3)$
Si nous analysons le système ci-dessus, nous pouvons voir que le système ne dépend que des valeurs futures du système c'est-à-dire que si nous mettons t = 0, il se réduira à x (3), qui est une valeur future. Ce système est un parfait exemple de système anti-causal.
Un système linéaire suit les lois de superposition. Cette loi est une condition nécessaire et suffisante pour prouver la linéarité du système. En dehors de cela, le système est une combinaison de deux types de lois -
- Loi d'additivité
- Loi d'homogénéité

La loi d'homogénéité et la loi d'additivité sont illustrées dans les figures ci-dessus. Cependant, il existe d'autres conditions pour vérifier si le système est linéaire ou non.
The conditions are -
- La sortie doit être zéro pour une entrée nulle.
- Aucun opérateur non linéaire ne doit être présent dans le système.
Exemples d'opérateurs non linéaires -
(a) Opérateurs trigonométriques - Sin, Cos, Tan, Cot, Sec, Cosec etc.
(b) Exponentiel, logarithmique, module, carré, cube, etc.
(c) sa (i / p), Sinc (i / p), Sqn (i / p) etc.
L'entrée x ou la sortie y ne doivent pas avoir ces opérateurs non linéaires.
Exemples
Voyons si les systèmes suivants sont linéaires.
a) $y(t) = x(t)+3$
Ce système n'est pas un système linéaire car il viole la première condition. Si nous mettons l'entrée à zéro, ce qui rend x (t) = 0, alors la sortie n'est pas nulle.
b) $y(t) = \sin tx(t)$
Dans ce système, si nous donnons une entrée égale à zéro, la sortie deviendra zéro. Par conséquent, la première condition est clairement remplie. Encore une fois, il n'y a pas d'opérateur non linéaire qui a été appliqué sur x (t). Par conséquent, la deuxième condition est également remplie. Par conséquent, le système est un système linéaire.
c) $y(t) = \sin (x(t))$
Dans le système ci-dessus, la première condition est satisfaite car si nous mettons x (t) = 0, la sortie sera également sin (0) = 0. Cependant, la deuxième condition n'est pas satisfaite, car il existe un opérateur non linéaire qui opère x (t). Par conséquent, le système n'est pas linéaire.
Si nous voulons définir ce système, nous pouvons dire que les systèmes, qui ne sont pas linéaires, sont des systèmes non linéaires. Il est clair que toutes les conditions qui ne sont pas respectées dans les systèmes linéaires doivent être satisfaites dans ce cas.
Conditions
La sortie ne doit pas être nulle lorsque l'entrée appliquée est nulle.
Tout opérateur non linéaire peut être appliqué sur l'entrée ou sur la sortie pour rendre le système non linéaire.
Exemples
Pour savoir si les systèmes donnés sont linéaires ou non linéaires.
a) $y(t) = e^{x(t)}$
Dans le système ci-dessus, la première condition est satisfaite car si nous rendons l'entrée nulle, la sortie est 1. De plus, un opérateur non linéaire exponentiel est appliqué à l'entrée. Clairement, il s'agit d'un cas de système non linéaire.
b) $y(t) = x(t+1)+x(t-1)$
Le type de système ci-dessus traite des valeurs passées et futures. Cependant, si nous rendons son entrée nulle, alors aucune de ses valeurs n'existe. Par conséquent, nous pouvons dire que si l'entrée est zéro, la version de l'entrée mise à l'échelle et décalée dans le temps sera également zéro, ce qui viole notre première condition. Là encore, il n'y a pas d'opérateur non linéaire présent. Par conséquent, la deuxième condition est également violée. De toute évidence, ce système n'est pas un système non linéaire; c'est plutôt un système linéaire.
Pour un système invariant dans le temps, la sortie et l'entrée doivent être retardées d'une certaine unité de temps. Tout retard fourni dans l'entrée doit être reflété dans la sortie pour un système invariant dans le temps.
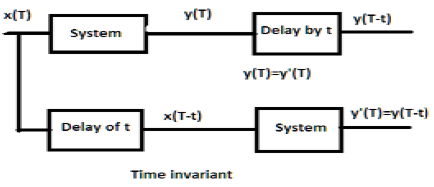
Exemples
a) $y(T) = x(2T)$
Si l'expression ci-dessus, elle est d'abord passée à travers le système, puis à travers la temporisation (comme indiqué dans la partie supérieure de la figure); alors la sortie deviendra$x(2T-2t)$. Maintenant, la même expression passe d'abord par un délai, puis par le système (comme indiqué dans la partie inférieure de la figure). La sortie deviendra$x(2T-t)$.
Par conséquent, le système n'est pas un système invariant dans le temps.
b) $y(T) = \sin [x(T)]$
Si le signal passe d'abord par le système puis par le processus de temporisation, la sortie est $\sin x(T-t)$. De même, si le système passe d'abord par la temporisation puis par le système, la sortie sera$\sin x(T-t)$. Nous pouvons voir clairement que les deux sorties sont identiques. Par conséquent, le système est invariant dans le temps.
Pour un système à variation de temps, la sortie et l'entrée doivent également être retardées d'une certaine constante de temps, mais le retard à l'entrée ne doit pas se refléter à la sortie. Tous les cas de mise à l'échelle temporelle sont des exemples de système de variante temporelle. De même, lorsque le coefficient dans la relation système est fonction du temps, le système est également une variante temporelle.
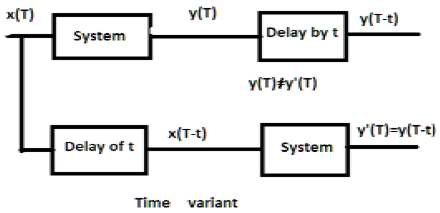
Exemples
a) $y(t) = x[\cos T]$
Si le signal ci-dessus est d'abord passé à travers le système, puis à travers la temporisation, la sortie sera $x\cos (T-t)$. S'il passe d'abord par la temporisation puis par le système, il sera$x(\cos T-t)$. Comme les sorties ne sont pas les mêmes, le système est en variante temporelle.
b) $y(T) = \cos T.x(T)$
Si l'expression ci-dessus est d'abord passée à travers le système, puis à travers la temporisation, la sortie sera $\cos(T-t)x(T-t)$. Cependant, si l'expression passe d'abord par la temporisation puis par le système, la sortie sera$\cos T.x(T-t)$. Comme les sorties ne sont pas les mêmes, il est clair que le système est variable dans le temps.
Un système stable satisfait la condition BIBO (entrée bornée pour sortie bornée). Ici, borné signifie fini en amplitude. Pour un système stable, la sortie doit être bornée ou finie, pour une entrée finie ou bornée, à chaque instant.
Quelques exemples d'entrées limitées sont des fonctions de sinus, cosinus, CC, signe et pas d'unité.
Exemples
a) $y(t) = x(t)+10$
Ici, pour une entrée bornée définie, nous pouvons obtenir une sortie bornée définie, c'est-à-dire si nous mettons $x(t) = 2, y(t) = 12$qui est limité dans la nature. Par conséquent, le système est stable.
b) $y(t) = \sin [x(t)]$
Dans l'expression donnée, nous savons que les fonctions sinus ont une limite de valeurs définie, qui se situe entre -1 et +1. Ainsi, quelles que soient les valeurs que nous substituerons à x (t), nous obtiendrons les valeurs dans notre limite. Par conséquent, le système est stable.
Les systèmes instables ne satisfont pas aux conditions BIBO. Par conséquent, pour une entrée bornée, nous ne pouvons pas nous attendre à une sortie bornée en cas de systèmes instables.
Exemples
a) $y(t) = tx(t)$
Ici, pour une entrée finie, on ne peut pas s'attendre à une sortie finie. Par exemple, si nous allons mettre$x(t) = 2 \Rightarrow y(t) = 2t$. Ce n'est pas une valeur finie car nous ne connaissons pas la valeur de t. Ainsi, il peut être varié de n'importe où. Par conséquent, ce système n'est pas stable. C'est un système instable.
b) $y(t) = \frac{x(t)}{\sin t}$
Nous avons discuté précédemment, que la fonction sinus a une plage définie de -1 à +1; mais ici, il est présent dans le dénominateur. Donc, dans le pire des cas, si nous mettons t = 0 et que la fonction sinus devient zéro, alors le système entier tendra vers l'infini. Par conséquent, ce type de système n'est pas du tout stable. De toute évidence, il s'agit d'un système instable.
Example 1 - Vérifiez si $y(t) = x*(t)$ est linéaire ou non linéaire.
Solution- La fonction représente le conjugué de l'entrée. Elle peut être vérifiée soit par la première loi d'homogénéité et la loi d'additivité, soit par les deux règles. Cependant, la vérification au moyen de règles est beaucoup plus facile, nous allons donc nous en tenir à cela.
Si l'entrée du système est égale à zéro, la sortie tend également vers zéro. Par conséquent, notre première condition est remplie. Il n'y a pas d'opérateur non linéaire utilisé ni en entrée ni en sortie. Par conséquent, le système est linéaire.
Example 2 - Vérifiez si $y(t)=\begin{cases}x(t+1), & t > 0\\x(t-1), & t\leq 0\end{cases}$ est linéaire ou non linéaire
Solution- Clairement, nous pouvons voir que lorsque le temps devient inférieur ou égal à zéro, l'entrée devient nulle. Ainsi, nous pouvons dire qu'à l'entrée zéro, la sortie est également nulle et notre première condition est satisfaite.
Là encore, aucun opérateur non linéaire n'est utilisé en entrée ni en sortie. Par conséquent, le système est linéaire.
Example 3 - Vérifiez si $y(t) = \sin t.x(t)$ est stable ou non.
Solution - Supposons que nous ayons pris la valeur de x (t) égale à 3. Ici, la fonction sinus a été multipliée par elle et la valeur maximale et minimale de la fonction sinus varie entre -1 et +1.
Par conséquent, la valeur maximale et minimale de la fonction entière variera également entre -3 et +3. Ainsi, le système est stable car ici nous obtenons une entrée bornée pour une sortie bornée.
La transformée de Fourier à temps discret (DTFT) existe pour les signaux d'énergie et de puissance. La transformée en Z n'existe pas non plus pour les signaux de type énergie ou puissance (NENP), jusqu'à un certain point seulement. Le remplacement$z=e^{jw}$ est utilisé pour la conversion de transformation Z en DTFT uniquement pour un signal absolument sommable.
Ainsi, la transformée en Z du signal de temps discret x (n) dans une série de puissance peut être écrite comme -
$$X(z) = \sum_{n-\infty}^\infty x(n)Z^{-n}$$L'équation ci-dessus représente une équation de transformation en Z à deux côtés.
Généralement, lorsqu'un signal est transformé en Z, il peut être représenté par -
$$X(Z) = Z[x(n)]$$Ou $x(n) \longleftrightarrow X(Z)$
S'il s'agit d'un signal temporel continu, les transformées en Z ne sont pas nécessaires car des transformations de Laplace sont utilisées. Cependant, les signaux temporels discrets ne peuvent être analysés que par des transformées en Z.
Région de convergence
La région de convergence est la plage de la variable complexe Z dans le plan Z. La transformation en Z du signal est finie ou convergente. Ainsi, ROC représente l'ensemble des valeurs de Z, pour lesquelles X (Z) a une valeur finie.
Propriétés de ROC
- Le ROC n'inclut aucun poteau.
- Pour le signal du côté droit, ROC sera à l'extérieur du cercle dans le plan Z.
- Pour le signal du côté gauche, ROC sera à l'intérieur du cercle dans le plan Z.
- Pour la stabilité, ROC inclut le cercle unitaire dans le plan Z.
- Pour le signal bilatéral, ROC est un anneau dans le plan Z.
- Pour un signal de durée finie, ROC est le plan Z entier.
La transformation en Z est uniquement caractérisée par -
- Expression de X (Z)
- ROC de X (Z)
Signaux et leur ROC
| x (n) | X (Z) | ROC |
|---|---|---|
| $\delta(n)$ | $1$ | Plan Z entier |
| $U(n)$ | $1/(1-Z^{-1})$ | Mod (Z)> 1 |
| $a^nu(n)$ | $1/(1-aZ^{-1})$ | Mod (Z)> Mod (a) |
| $-a^nu(-n-1)$ | $1/(1-aZ^{-1})$ | Mod (Z) <Mod (a) |
| $na^nu(n)$ | $aZ^{-1}/(1-aZ^{-1})^2$ | Mod (Z)> Mod (a) |
| $-a^nu(-n-1)$ | $aZ^{-1}/(1-aZ^{-1})^2$ | Mod (Z) <Mod (a) |
| $U(n)\cos \omega n$ | $(Z^2-Z\cos \omega)/(Z^2-2Z \cos \omega +1)$ | Mod (Z)> 1 |
| $U(n)\sin \omega n$ | $(Z\sin \omega)/(Z^2-2Z \cos \omega +1)$ | Mod (Z)> 1 |
Exemple
Trouvons la transformée Z et le ROC d'un signal donné comme $x(n) = \lbrace 7,3,4,9,5\rbrace$, où l'origine de la série est à 3.
Solution - Appliquer la formule que nous avons -
$X(z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$
$= \sum_{n=-1}^3 x(n)Z^{-n}$
$= x(-1)Z+x(0)+x(1)Z^{-1}+x(2)Z^{-2}+x(3)Z^{-3}$
$= 7Z+3+4Z^{-1}+9Z^{-2}+5Z^{-3}$
ROC est le plan Z entier à l'exclusion de Z = 0, ∞, -∞
Dans ce chapitre, nous allons comprendre les propriétés de base des transformations en Z.
Linéarité
Il indique que lorsque deux ou plusieurs signaux discrets individuels sont multipliés par des constantes, leurs transformées en Z respectives seront également multipliées par les mêmes constantes.
Mathématiquement,
$$a_1x_1(n)+a_2x_2(n) = a_1X_1(z)+a_2X_2(z)$$Proof - Nous savons que,
$$X(Z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$$$= \sum_{n=-\infty}^\infty (a_1x_1(n)+a_2x_2(n))Z^{-n}$
$= a_1\sum_{n = -\infty}^\infty x_1(n)Z^{-n}+a_2\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$
$= a_1X_1(z)+a_2X_2(z)$ (Par conséquent prouvé)
Ici, le ROC est $ROC_1\bigcap ROC_2$.
Changement de temps
La propriété de décalage temporel décrit comment le changement dans le domaine temporel dans le signal discret affectera le domaine Z, qui peut être écrit comme;
$$x(n-n_0)\longleftrightarrow X(Z)Z^{-n}$$Ou $x(n-1)\longleftrightarrow Z^{-1}X(Z)$
Proof -
Laisser $y(P) = X(P-K)$
$Y(z) = \sum_{p = -\infty}^\infty y(p)Z^{-p}$
$= \sum_{p = -\infty}^\infty (x(p-k))Z^{-p}$
Soit s = pk
$= \sum_{s = -\infty}^\infty x(s)Z^{-(s+k)}$
$= \sum_{s = -\infty}^\infty x(s)Z^{-s}Z^{-k}$
$= Z^{-k}[\sum_{s=-\infty}^\infty x(m)Z^{-s}]$
$= Z^{-k}X(Z)$ (Par conséquent prouvé)
Ici, ROC peut être écrit comme Z = 0 (p> 0) ou Z = ∞ (p <0)
Exemple
U (n) et U (n-1) peuvent être tracés comme suit
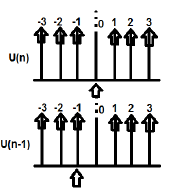
La transformation en Z de U (n) cab s'écrit;
$\sum_{n = -\infty}^\infty [U(n)]Z^{-n} = 1$
La transformation Z de U (n-1) peut s'écrire;
$\sum_{n = -\infty}^\infty [U(n-1)]Z^{-n} = Z^{-1}$
Donc ici $x(n-n_0) = Z^{-n_0}X(Z)$ (Par conséquent prouvé)
Mise à l'échelle du temps
La propriété de mise à l'échelle du temps nous indique quel sera le domaine Z du signal lorsque le temps est mis à l'échelle sous sa forme discrète, qui peut s'écrire;
$$a^nx(n) \longleftrightarrow X(a^{-1}Z)$$Proof -
Laisser $y(p) = a^{p}x(p)$
$Y(P) = \sum_{p=-\infty}^\infty y(p)Z^{-p}$
$= \sum_{p=-\infty}^\infty a^px(p)Z^{-p}$
$= \sum_{p=-\infty}^\infty x(p)[a^{-1}Z]^{-p}$
$= X(a^{-1}Z)$(Par conséquent prouvé)
ROC: = Mod (ar1) <Mod (Z) <Mod (ar2) où Mod = Module
Exemple
Déterminons la transformation en Z de $x(n) = a^n \cos \omega n$ en utilisant la propriété Time scaling.
Solution -
Nous savons déjà que la transformation en Z du signal $\cos (\omega n)$ est donné par -
$$\sum_{n=-\infty}^\infty(\cos \omega n)Z^{-n} = (Z^2-Z \cos \omega)/(Z^2-2Z\cos \omega +1)$$
Maintenant, en appliquant la propriété Time scaling, la transformation Z de $a^n \cos \omega n$ peut être écrit comme;
$\sum_{n=-\infty}^\infty(a^n\cos \omega n)Z^{-n} = X(a^{-1}Z)$
$= [(a^{-1}Z)^2-(a^{-1}Z \cos \omega n)]/((a^{-1}Z)^2-2(a^{-1}Z \cos \omega n)+1)$
$= Z(Z-a \cos \omega)/(Z^2-2az \cos \omega+a^2)$
Différenciation successive
La propriété de différenciation successive montre que la transformée en Z aura lieu lorsque nous différencierons le signal discret dans le domaine temporel, par rapport au temps. Ceci est montré comme ci-dessous.
$$\frac{dx(n)}{dn} = (1-Z^{-1})X(Z)$$Proof -
Considérez la LHS de l'équation - $\frac{dx(n)}{dn}$
$$= \frac{[x(n)-x(n-1)]}{[n-(n-1)]}$$$= x(n)-X(n-1)$
$= x(Z)-Z^{-1}x(Z)$
$= (1-Z^{-1})x(Z)$ (Par conséquent prouvé)
ROC: R1 <Mod (Z) <R2
Exemple
Trouvons la transformée en Z d'un signal donné par $x(n) = n^2u(n)$
Par propriété on peut écrire
$Zz[nU(n)] = -Z\frac{dZ[U(n)]}{dz}$
$= -Z\frac{d[\frac{Z}{Z-1}]}{dZ}$
$= Z/((Z-1)^2$
$= y(let)$
Maintenant, Z [ny] peut être découvert en appliquant à nouveau la propriété,
$Z(n,y) = -Z\frac{dy}{dz}$
$= -Z\frac{d[Z/(Z-1)^3]}{dz}$
$= Z(Z+1)/(Z-1)^2$
Convolution
Cela représente le changement dans le domaine Z du système lorsqu'une convolution a lieu sous la forme de signal discret, qui peut s'écrire -
$x_1(n)*x_2(n) \longleftrightarrow X_1(Z).X_2(Z)$
Proof -
$X(Z) = \sum_{n = -\infty}^\infty x(n)Z^{-n}$
$= \sum_{n=-\infty}^\infty[\sum_{k = -\infty}^\infty x_1(k)x_2(n-k)]Z^{-n}$
$= \sum_{k = -\infty}^\infty x_1(k)[\sum_n^\infty x_2(n-k)Z^{-n}]$
$= \sum_{k = -\infty}^\infty x_1(k)[\sum_{n = -\infty}^\infty x_2(n-k)Z^{-(n-k)}Z^{-k}]$
Soit nk = l, alors l'équation ci-dessus cab s'écrit -
$X(Z) = \sum_{k = -\infty}^\infty x_1(k)[Z^{-k}\sum_{l=-\infty}^\infty x_2(l)Z^{-l}]$
$= \sum_{k = -\infty}^\infty x_1(k)X_2(Z)Z^{-k}$
$= X_2(Z)\sum_{k = -\infty}^\infty x_1(Z)Z^{-k}$
$= X_1(Z).X_2(Z)$ (Par conséquent prouvé)
ROC:$ROC\bigcap ROC2$
Exemple
Trouvons la convolution donnée par deux signaux
$x_1(n) = \lbrace 3,-2,2\rbrace$ ... (équation 1)
$x_2(n) = \lbrace 2,0\leq 4\quad and\quad 0\quad elsewhere\rbrace$ ... (équation 2)
La transformation en Z de la première équation peut s'écrire;
$\sum_{n = -\infty}^\infty x_1(n)Z^{-n}$
$= 3-2Z^{-1}+2Z^{-2}$
La transformation en Z du deuxième signal peut être écrite comme;
$\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$
$= 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$
Ainsi, la convolution des deux signaux ci-dessus est donnée par -
$X(Z) = [x_1(Z)^*x_2(Z)]$
$= [3-2Z^{-1}+2Z^{-2}]\times [2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}]$
$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+...\quad...\quad...$
En prenant la transformation en Z inverse que nous obtenons,
$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$
Théorème de la valeur initiale
Si x (n) est une séquence causale, qui a sa transformation Z comme X (z), alors le théorème de valeur initiale peut être écrit comme;
$X(n)(at\quad n = 0) = \lim_{z \to \infty} X(z)$
Proof - Nous savons que,
$X(Z) = \sum_{n = 0} ^\infty x(n)Z^{-n}$
En élargissant la série ci-dessus, nous obtenons;
$= X(0)Z^0+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$
$= X(0)\times 1+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$
Dans le cas ci-dessus si Z → ∞ alors $Z^{-n}\rightarrow 0$ (Parce que n> 0)
Par conséquent, nous pouvons dire;
$\lim_{z \to \infty}X(z) = X(0)$ (Par conséquent prouvé)
Théorème de la valeur finale
Le théorème de la valeur finale stipule que si la transformée en Z d'un signal est représentée par X (Z) et que les pôles sont tous à l'intérieur du cercle, alors sa valeur finale est notée x (n) ou X (∞) et peut être écrite comme -
$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$
Conditions -
- Il n'est applicable que pour les systèmes causaux.
- $X(Z)(1-Z^{-1})$ devrait avoir des pôles à l'intérieur du cercle unitaire dans le plan Z.
Proof - Nous savons que
$Z^+[x(n+1)-x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$
$\Rightarrow Z^+[x(n+1)]-Z^+[x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$
$\Rightarrow Z[X(Z)^+-x(0)]-X(Z)^+ = \lim_{k \to \infty}\sum_{n = 0}^kZ^{-n}[x(n+1)-x(n)]$
Ici, nous pouvons appliquer la propriété avancée de la transformation en Z unilatérale. Ainsi, l'équation ci-dessus peut être réécrite comme;
$Z^+[x(n+1)] = Z[X(2)^+-x(0)Z^0] = Z[X(Z)^+-x(0)]$
En mettant maintenant z = 1 dans l'équation ci-dessus, nous pouvons développer l'équation ci-dessus -
$\lim_{k \to \infty}{[x(1)-x(0)+x(6)-x(1)+x(3)-x(2)+...\quad...\quad...+x(x+1)-x(k)]}$
Cela peut être formulé comme suit:
$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$(Par conséquent prouvé)
Exemple
Trouvons la valeur initiale et finale de x (n) dont le signal est donné par
$X(Z) = 2+3Z^{-1}+4Z^{-2}$
Solution - Trouvons d'abord la valeur initiale du signal en appliquant le théorème
$x(0) = \lim_{z \to \infty}X(Z)$
$= \lim_{z \to \infty}[2+3Z^{-1}+4Z^{-2}]$
$= 2+(\frac{3}{\infty})+(\frac{4}{\infty}) = 2$
Trouvons maintenant la valeur finale du signal en appliquant le théorème
$x(\infty) = \lim_{z \to \infty}[(1-Z^{-1})X(Z)]$
$= \lim_{z \to \infty}[(1-Z^{-1})(2+3Z^{-1}+4Z^{-2})]$
$= \lim_{z \to \infty}[2+Z^{-1}+Z^{-2}-4Z^{-3}]$
$= 2+1+1-4 = 0$
Some other properties of Z-transform are listed below -
Différenciation en fréquence
Il donne le changement de domaine Z du signal, lorsque son signal discret est différencié par rapport au temps.
$nx(n)\longleftrightarrow -Z\frac{dX(z)}{dz}$
Son ROC peut s'écrire;
$r_2< Mod(Z)< r_1$
Exemple
Trouvons la valeur de x (n) par Différenciation en fréquence, dont le signal discret dans le domaine Z est donné par $x(n)\longleftrightarrow X(Z) = log(1+aZ^{-1})$
Par propriété, on peut écrire que
$nx(n)\longleftrightarrow -Z\frac{dx(Z)}{dz}$
$= -Z[\frac{-aZ^{-2}}{1+aZ^{-1}}]$
$= (aZ^{-1})/(1+aZ^{-1})$
$= 1-1/(1+aZ^{-1})$
$nx(n) = \delta(n)-(-a)^nu(n)$
$\Rightarrow x(n) = 1/n[\delta(n)-(-a)^nu(n)]$
Multiplication dans le temps
Il donne le changement du domaine Z du signal lorsque la multiplication a lieu au niveau du signal discret.
$x_1(n).x_2(n)\longleftrightarrow(\frac{1}{2\Pi j})[X1(Z)*X2(Z)]$
Conjugaison dans le temps
Cela représente la représentation du signal discret conjugué dans le domaine Z.
$X^*(n)\longleftrightarrow X^*(Z^*)$
Un système qui a une fonction système ne peut être stable que si tous les pôles se trouvent à l'intérieur du cercle unitaire. Tout d'abord, nous vérifions si le système est causal ou non. Si le système est Causal, alors nous allons pour sa détermination de stabilité BIBO; où la stabilité BIBO fait référence à l'entrée bornée pour la condition de sortie bornée.
Cela peut être écrit comme;
$Mod(X(Z))< \infty$
$= Mod(\sum x(n)Z^{-n})< \infty$
$= \sum Mod(x(n)Z^{-n})< \infty$
$= \sum Mod[x(n)(re^{jw})^{-n}]< 0$
$= \sum Mod[x(n)r^{-n}]Mod[e^{-jwn}]< \infty$
$= \sum_{n = -\infty}^\infty Mod[x(n)r^{-n}]< \infty$
L'équation ci-dessus montre la condition d'existence de la transformée en Z.
Cependant, la condition d'existence du signal DTFT est
$$\sum_{n = -\infty}^\infty Mod(x(n)< \infty$$Exemple 1
Essayons de trouver la transformée en Z du signal, qui est donnée par
$x(n) = -(-0.5)^{-n}u(-n)+3^nu(n)$
$= -(-2)^nu(n)+3^nu(n)$
Solution - Ici, pour $-(-2)^nu(n)$ le ROC est à gauche et Z <2
Pour $3^nu(n)$ ROC est du côté droit et Z> 3
Par conséquent, ici la transformée Z du signal n'existera pas car il n'y a pas de région commune.
Exemple 2
Essayons de trouver la transformée en Z du signal donné par
$x(n) = -2^nu(-n-1)+(0.5)^nu(n)$
Solution - Ici, pour $-2^nu(-n-1)$ ROC du signal est à gauche et Z <2
Pour le signal $(0.5)^nu(n)$ ROC est du côté droit et Z> 0,5
Ainsi, le ROC commun étant formé comme 0,5 <Z <2
Par conséquent, la transformée Z peut être écrite comme;
$X(Z) = \lbrace\frac{1}{1-2Z^{-1}}\rbrace+\lbrace\frac{1}{(1-0.5Z)^{-1}}\rbrace$
Exemple 3
Essayons de trouver la transformée en Z du signal, qui est donnée par $x(n) = 2^{r(n)}$
Solution- r (n) est le signal de rampe. Ainsi, le signal peut être écrit comme;
$x(n) = 2^{nu(n)}\lbrace 1, n<0 (u(n)=0)\quad and\quad2^n, n\geq 0(u(n) = 1)\rbrace$
$= u(-n-1)+2^nu(n)$
Ici, pour le signal $u(-n-1)$ et ROC Z <1 et pour $2^nu(n)$ avec ROC est Z> 2.
Ainsi, la transformation en Z du signal n'existera pas.
Z -Transform pour le système causal
Le système causal peut être défini comme $h(n) = 0,n<0$. Pour le système causal, ROC sera à l'extérieur du cercle dans le plan Z.
$H(Z) = \displaystyle\sum\limits_{n = 0}^{\infty}h(n)Z^{-n}$
Élargir l'équation ci-dessus,
$H(Z) = h(0)+h(1)Z^{-1}+h(2)Z^{-2}+...\quad...\quad...$
$= N(Z)/D(Z)$
Pour les systèmes causaux, l'expansion de la fonction de transfert n'inclut pas les puissances positives de Z. Pour le système causal, l'ordre du numérateur ne peut pas dépasser l'ordre du dénominateur. Cela peut être écrit comme-
$\lim_{z \rightarrow \infty}H(Z) = h(0) = 0\quad or\quad Finite$
Pour la stabilité du système causal, les pôles de la fonction de transfert doivent être à l'intérieur du cercle unitaire dans le plan Z.
Transformée en Z pour le système anti-causal
Le système anti-causal peut être défini comme $h(n) = 0, n\geq 0$. Pour le système anti-causal, les pôles de la fonction de transfert doivent se trouver à l'extérieur du cercle unitaire dans le plan Z. Pour le système anti-causal, ROC sera à l'intérieur du cercle dans le plan Z.
Si nous voulons analyser un système, qui est déjà représenté dans le domaine fréquentiel, en tant que signal de temps discret, nous optons pour une transformation Z inversée.
Mathématiquement, il peut être représenté par;
$$x(n) = Z^{-1}X(Z)$$où x (n) est le signal dans le domaine temporel et X (Z) est le signal dans le domaine fréquentiel.
Si nous voulons représenter l'équation ci-dessus en format intégral, nous pouvons l'écrire comme
$$x(n) = (\frac{1}{2\Pi j})\oint X(Z)Z^{-1}dz$$Ici, l'intégrale est sur un chemin fermé C. Ce chemin est dans le ROC du x (z) et il contient l'origine.
Méthodes pour trouver la transformation en Z inversée
Lorsque l'analyse est nécessaire dans un format discret, nous convertissons le signal du domaine fréquentiel en un format discret par transformation en Z inverse. Nous suivons les quatre méthodes suivantes pour déterminer la transformation en Z inverse.
- Méthode de division longue
- Méthode d'expansion partielle des fractions
- Méthode intégrale des résidus ou des contours
Méthode de division longue
Dans cette méthode, la transformée Z du signal x (z) peut être représentée comme le rapport du polynôme comme indiqué ci-dessous;
$$x(z)=N(Z)/D(Z)$$Maintenant, si nous continuons à diviser le numérateur par le dénominateur, nous obtiendrons une série comme indiqué ci-dessous
$$X(z) = x(0)+x(1)Z^{-1}+x(2)Z^{-2}+...\quad...\quad...$$La séquence ci-dessus représente la série de transformée en Z inverse du signal donné (pour n ≥ 0) et le système ci-dessus est causal.
Cependant pour n <0, la série peut être écrite comme;
$$x(z) = x(-1)Z^1+x(-2)Z^2+x(-3)Z^3+...\quad...\quad...$$Méthode d'expansion partielle des fractions
Ici aussi, le signal est d'abord exprimé sous la forme N (z) / D (z).
S'il s'agit d'une fraction rationnelle, elle sera représentée comme suit;
$x(z) = b_0+b_1Z^{-1}+b_2Z^{-2}+...\quad...\quad...+b_mZ^{-m})/(a_0+a_1Z^{-1}+a_2Z^{-2}+...\quad...\quad...+a_nZ^{-N})$
Celui ci-dessus est incorrect lorsque m <n et an ≠ 0
Si le rapport n'est pas correct (c'est-à-dire incorrect), nous devons le convertir sous la forme appropriée pour le résoudre.
Méthode intégrale des résidus ou des contours
Dans cette méthode, nous obtenons une transformée Z inverse x (n) en additionnant les résidus de $[x(z)Z^{n-1}]$à tous les pôles. Mathématiquement, cela peut être exprimé par
$$x(n) = \displaystyle\sum\limits_{all\quad poles\quad X(z)}residues\quad of[x(z)Z^{n-1}]$$Ici, le résidu pour tout pôle d'ordre m à $z = \beta$ est
$$Residues = \frac{1}{(m-1)!}\lim_{Z \rightarrow \beta}\lbrace \frac{d^{m-1}}{dZ^{m-1}}\lbrace (z-\beta)^mX(z)Z^{n-1}\rbrace$$Exemple 1
Trouvez la réponse du système $s(n+2)-3s(n+1)+2s(n) = \delta (n)$, lorsque toutes les conditions initiales sont nulles.
Solution - En prenant Z-transform des deux côtés de l'équation ci-dessus, nous obtenons
$$S(z)Z^2-3S(z)Z^1+2S(z) = 1$$$\Rightarrow S(z)\lbrace Z^2-3Z+2\rbrace = 1$
$\Rightarrow S(z) = \frac{1}{\lbrace z^2-3z+2\rbrace}=\frac{1}{(z-2)(z-1)} = \frac{\alpha _1}{z-2}+\frac{\alpha _2}{z-1}$
$\Rightarrow S(z) = \frac{1}{z-2}-\frac{1}{z-1}$
En prenant la transformée en Z inverse de l'équation ci-dessus, nous obtenons
$S(n) = Z^{-1}[\frac{1}{Z-2}]-Z^{-1}[\frac{1}{Z-1}]$
$= 2^{n-1}-1^{n-1} = -1+2^{n-1}$
Exemple 2
Trouvez la fonction système H (z) et la réponse de l'échantillon unitaire h (n) du système dont l'équation de différence est décrite sous
$y(n) = \frac{1}{2}y(n-1)+2x(n)$
où, y (n) et x (n) sont respectivement la sortie et l'entrée du système.
Solution - En prenant la transformée en Z de l'équation de différence ci-dessus, nous obtenons
$y(z) = \frac{1}{2}Z^{-1}Y(Z)+2X(z)$
$= Y(Z)[1-\frac{1}{2}Z^{-1}] = 2X(Z)$
$= H(Z) = \frac{Y(Z)}{X(Z)} = \frac{2}{[1-\frac{1}{2}Z^{-1}]}$
Ce système a un pôle à $Z = \frac{1}{2}$ et $Z = 0$ et $H(Z) = \frac{2}{[1-\frac{1}{2}Z^{-1}]}$
Par conséquent, en prenant la transformée Z inverse de ce qui précède, nous obtenons
$h(n) = 2(\frac{1}{2})^nU(n)$
Exemple 3
Déterminer Y (z), n≥0 dans le cas suivant -
$y(n)+\frac{1}{2}y(n-1)-\frac{1}{4}y(n-2) = 0\quad given\quad y(-1) = y(-2) = 1$
Solution - En appliquant la transformation en Z à l'équation ci-dessus, nous obtenons
$Y(Z)+\frac{1}{2}[Z^{-1}Y(Z)+Y(-1)]-\frac{1}{4}[Z^{-2}Y(Z)+Z^{-1}Y(-1)+4(-2)] = 0$
$\Rightarrow Y(Z)+\frac{1}{2Z}Y(Z)+\frac{1}{2}-\frac{1}{4Z^2}Y(Z)-\frac{1}{4Z}-\frac{1}{4} = 0$
$\Rightarrow Y(Z)[1+\frac{1}{2Z}-\frac{1}{4Z^2}] =\frac{1}{4Z}-\frac{1}{2}$
$\Rightarrow Y(Z)[\frac{4Z^2+2Z-1}{4Z^2}] = \frac{1-2Z}{4Z}$
$\Rightarrow Y(Z) = \frac{Z(1-2Z)}{4Z^2+2Z-1}$
Comme la transformée de Fourier du signal en temps continu, la transformée de Fourier en temps discret peut être utilisée pour représenter une séquence discrète dans sa représentation de domaine de fréquence équivalente et son système de temps discret LTI et pour développer divers algorithmes de calcul.
X (jω) en FT continu, est une fonction continue de x (n). Cependant, DFT s'occupe de représenter x (n) avec des échantillons de son spectre X (ω). Par conséquent, cet outil mathématique revêt une grande importance sur le plan informatique dans la représentation pratique. Les séquences périodiques et non périodiques peuvent être traitées via cet outil. Les séquences périodiques doivent être échantillonnées en étendant la période à l'infini.
Échantillonnage dans le domaine fréquentiel
Dès l'introduction, il est clair que nous devons savoir comment procéder par échantillonnage dans le domaine fréquentiel c'est-à-dire échantillonnage X (ω). Par conséquent, la relation entre la transformée de Fourier échantillonnée et la DFT est établie de la manière suivante.
De même, des séquences périodiques peuvent s'adapter à cet outil en étendant la période N à l'infini.
Soit une suite non périodique, $X(n) = \lim_{N \to \infty}x_N(n)$
Définition de sa transformée de Fourier,
$X(\omega ) = \sum_{n=-\infty}^\infty x(n)e^{-jwn}X(K\delta \omega)$
Ici, X (ω) est échantillonné périodiquement, à chaque intervalle de δω radian.
Comme X (ω) est périodique en 2π radians, nous n'avons besoin d'échantillons que dans la gamme fondamentale. Les échantillons sont prélevés après des intervalles équidistants dans la gamme de fréquences 0≤ω≤2π. L'espacement entre les intervalles équivalents est$\delta \omega = \frac{2\pi }{N}k$ radian.
En cours d'évaluation, $\omega = \frac{2\pi}{N}k$
$X(\frac{2\pi}{N}k) = \sum_{n = -\infty}^\infty x(n)e^{-j2\pi nk/N},$ ... éq (2)
où k = 0,1, …… N-1
Après avoir subdivisé ce qui précède et changé l'ordre de sommation
$X(\frac{2\pi}{N}k) = \displaystyle\sum\limits_{n = 0}^{N-1}[\displaystyle\sum\limits_{l = -\infty}^\infty x(n-Nl)]e^{-j2\pi nk/N}$ ... éq (3)
$\sum_{l=-\infty}^\infty x(n-Nl) = x_p(n) = a\quad periodic\quad function\quad of\quad period\quad N\quad and\quad its\quad fourier\quad series\quad = \sum_{k = 0}^{N-1}C_ke^{j2\pi nk/N}$
où, n = 0,1,… .., N-1; 'p' - signifie entité ou fonction périodique
Les coefficients de Fourier sont,
$C_k = \frac{1}{N}\sum_{n = 0}^{N-1}x_p(n)e^{-j2\pi nk/N}$k = 0,1,…, N-1 ... eq (4)
En comparant les équations 3 et 4, nous obtenons;
$NC_k = X(\frac{2\pi}{N}k)$k = 0,1,…, N-1 ... eq (5)
$NC_k = X(\frac{2\pi}{N}k) = X(e^{jw}) = \displaystyle\sum\limits_{n = -\infty}^\infty x_p(n)e^{-j2\pi nk/N}$... éq (6)
De l'expansion de la série Fourier,
$x_p(n) = \frac{1}{N}\displaystyle\sum\limits_{k = 0}^{N-1}NC_ke^{j2\pi nk/N} = \frac{1}{N}\sum_{k = 0}^{N-1}X(\frac{2\pi}{N}k)e^{j2\pi nk/N}$... éq (7)
Où n = 0,1,…, N-1
Ici, nous avons obtenu le signal périodique de X (ω). $x(n)$ peut être extrait de $x_p(n)$ uniquement, s'il n'y a pas d'alias dans le domaine temporel. $N\geq L$
N = période de $x_p(n)$ L = période de $x(n)$
$x(n) = \begin{cases}x_p(n), & 0\leq n\leq N-1\\0, & Otherwise\end{cases}$
La cartographie est réalisée de cette manière.
Propriétés de DFT
Linéarité
Il déclare que la DFT d'une combinaison de signaux est égale à la somme des DFT des signaux individuels. Prenons deux signaux x 1 (n) et x 2 (n), dont les DFT sont respectivement X 1 (ω) et X 2 (ω). Donc si
$x_1(n)\rightarrow X_1(\omega)$et$x_2(n)\rightarrow X_2(\omega)$
ensuite $ax_1(n)+bx_2(n)\rightarrow aX_1(\omega)+bX_2(\omega)$
où a et b sont des constantes.
Symétrie
Les propriétés de symétrie de DFT peuvent être dérivées de la même manière que nous avons dérivé les propriétés de symétrie DTFT. On sait que la DFT de séquence x (n) est notée X (K). Maintenant, si x (n) et X (K) sont des séquences de valeurs complexes, alors elles peuvent être représentées sous
$x(n) = x_R(n)+jx_1(n),0\leq n\leq N-1$
Et $X(K) = X_R(K)+jX_1(K),0\leq K\leq N-1$
Propriété de la dualité
Considérons un signal x (n), dont la DFT est donnée par X (K). Soit la séquence de durée finie X (N). Alors selon le théorème de dualité,
Si, $x(n)\longleftrightarrow X(K)$
Ensuite, $X(N)\longleftrightarrow Nx[((-k))_N]$
Donc, en utilisant ce théorème si nous connaissons DFT, nous pouvons facilement trouver la séquence de durée finie.
Propriétés conjuguées complexes
Supposons qu'il y ait un signal x (n), dont la DFT nous est également connue sous le nom de X (K). Maintenant, si le conjugué complexe du signal est donné comme x * (n), alors nous pouvons facilement trouver la DFT sans faire beaucoup de calcul en utilisant le théorème ci-dessous.
Si, $x(n)\longleftrightarrow X(K)$
Ensuite, $x*(n)\longleftrightarrow X*((K))_N = X*(N-K)$
Décalage de fréquence circulaire
La multiplication de la séquence x (n) par la séquence exponentielle complexe $e^{j2\Pi kn/N}$équivaut au décalage circulaire de la DFT par unités L en fréquence. Il s'agit du double de la propriété de décalage temporel circulaire.
Si, $x(n)\longleftrightarrow X(K)$
Ensuite, $x(n)e^{j2\Pi Kn/N}\longleftrightarrow X((K-L))_N$
Multiplication de deux séquences
S'il y a deux signaux x 1 (n) et x 2 (n) et que leurs DFT respectifs sont X 1 (k) et X 2 (K), alors la multiplication des signaux en séquence temporelle correspond à la convolution circulaire de leurs DFT.
Si, $x_1(n)\longleftrightarrow X_1(K)\quad\&\quad x_2(n)\longleftrightarrow X_2(K)$
Ensuite, $x_1(n)\times x_2(n)\longleftrightarrow X_1(K)© X_2(K)$
Théorème de Parseval
Pour les suites complexes x (n) et y (n), en général
Si, $x(n)\longleftrightarrow X(K)\quad \&\quad y(n)\longleftrightarrow Y(K)$
Ensuite, $\sum_{n = 0}^{N-1}x(n)y^*(n) = \frac{1}{N}\sum_{k = 0}^{N-1}X(K)Y^*(K)$
Nous savons que quand $\omega = 2\pi K/N$ et $N\rightarrow \infty,\omega$ devient une variable continue et la somme des limites devient $-\infty$ à $+\infty$.
Par conséquent,
$$NC_k = X(\frac{2\pi}{N}k) = X(e^{j\omega}) = \displaystyle\sum\limits_{n = -\infty}^\infty x(n)e^{\frac{-j2\pi nk}{N}} = \displaystyle\sum\limits_{n = -\infty}^\infty x(n)e^{-j\omega n}$$Transformée de Fourier en temps discret (DTFT)
Nous savons que, $X(e^{j\omega}) = \sum_{n = -\infty}^\infty x(n)e^{-j\omega n}$
Où, $X(e^{j\omega})$est continue et périodique en ω et de période 2π. … Éq (1)
Maintenant,
$x_p(n) = \sum_{k = 0}^{N-1}NC_ke^{j2 \pi nk/N}$ … De la série Fourier
$x_p(n) = \frac{1}{2\pi}\sum_{k=0}^{N-1}NC_ke^{j2\pi nk/N}\times \frac{2\pi}{N}$
ω devient continu et $\frac{2\pi}{N}\rightarrow d\omega$, pour les raisons citées ci-dessus.
$x(n) = \frac{1}{2\pi}\int_{n = 0}^{2\pi}X(e^{j\omega})e^{j\omega n}d\omega$… Éq (2)
Transformée de Fourier en temps discret inverse
Symboliquement,
$x(n)\Longleftrightarrow x(e^{j\omega})$(La paire de transformées de Fourier)
La condition nécessaire et suffisante pour l'existence d'une transformée de Fourier en temps discret pour une séquence non périodique x (n) est sommable en absolu.
c'est à dire$\sum_{n = -\infty}^\infty|x(n)|<\infty$
Propriétés de DTFT
Linearity : $a_1x_1(n)+a_2x_2(n)\Leftrightarrow a_1X_1(e^{j\omega})+a_2X_2(e^{j\omega})$
Time shifting - $x(n-k)\Leftrightarrow e^{-j\omega k}.X(e^{j\omega})$
Time Reversal - $x(-n)\Leftrightarrow X(e^{-j\omega})$
Frequency shifting - $e^{j\omega _0n}x(n)\Leftrightarrow X(e^{j(\omega -\omega _0)})$
Differentiation frequency domain - $nx(n) = j\frac{d}{d\omega}X(e^{j\omega})$
Convolution - $x_1(n)*x_2(n)\Leftrightarrow X_1(e^{j\omega})\times X_2(e^{j\omega})$
Multiplication - $x_1(n)\times x_2(n)\Leftrightarrow X_1(e^{j\omega})*X_2(e^{j\omega})$
Co-relation - $y_{x_1\times x_2}(l)\Leftrightarrow X_1(e^{j\omega})\times X_2(e^{j\omega})$
Modulation theorem - $x(n)\cos \omega _0n = \frac{1}{2}[X_1(e^{j(\omega +\omega _0})*X_2(e^{jw})$
Symmetry -$x^*(n)\Leftrightarrow X^*(e^{-j\omega})$ ;
$x^*(-n)\Leftrightarrow X^*(e^{j\omega})$ ;
$Real[x(n)]\Leftrightarrow X_{even}(e^{j\omega})$ ;
$Imag[x(n)]\Leftrightarrow X_{odd}(e^{j\omega})$ ;
$x_{even}(n)\Leftrightarrow Real[x(e^{j\omega})]$ ;
$x_{odd}(n)\Leftrightarrow Imag[x(e^{j\omega})]$ ;
Parseval’s theorem - $\sum_{-\infty}^\infty|x_1(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X_1(e^{j\omega})|^2d\omega$
Plus tôt, nous avons étudié l'échantillonnage dans le domaine fréquentiel. Avec ces connaissances de base, nous échantillonnons$X(e^{j\omega})$dans le domaine fréquentiel, de sorte qu'une analyse numérique pratique puisse être effectuée à partir de ces données échantillonnées. Par conséquent, la DFT est échantillonnée à la fois dans le domaine temporel et fréquentiel. Avec l'hypothèse$x(n) = x_p(n)$
Par conséquent, DFT est donné par -
$X(k) = DFT[x(n)] = X(\frac{2\pi}{N}k) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{-\frac{j2\pi nk}{N}}$, k = 0,1,…., N − 1 … éq (3)
Et IDFT est donné par -
$X(n) = IDFT[X(k)] = \frac{1}{N}\sum_{k = 0}^{N-1}X(k)e^{\frac{j2\pi nk}{N}}$, n = 0,1,…., N − 1 … éq (4)
$\therefore x(n)\Leftrightarrow X(k)$
Facteur Twiddle
Il est noté $W_N$ et défini comme $W_N = e^{-j2\pi /N}$. Son ampleur est toujours maintenue à l'unité. Phase de$W_N = -2\pi /N$. C'est un vecteur sur le cercle unitaire et est utilisé pour la commodité du calcul. Mathématiquement, il peut être montré comme -
$W_N^r = W_N^{r\pm N} = W_N^{r\pm 2N} = ...$
Elle est fonction de r et de la période N.
Considérons N = 8, r = 0,1,2,3,… .14,15,16,….
$\Longleftrightarrow W_8^0 = W_8^8 = W_8^{16} = ... = ... = W_8^{32} = ... =1= 1\angle 0$
$W_8^1 = W_8^9 = W_8^{17} = ... = ... = W_8^{33} = ... =\frac{1}{\sqrt 2}= j\frac{1}{\sqrt 2} = 1\angle-\frac{\pi}{4}$
Transformation linéaire
Comprenons la transformation linéaire -
Nous savons que,
$DFT(k) = DFT[x(n)] = X(\frac{2\pi}{N}k) = \sum_{n = 0}^{N-1}x(n).W_n^{-nk};\quad k = 0,1,….,N−1$
$x(n) = IDFT[X(k)] = \frac{1}{N}\sum_{k = 0}^{N-1}X(k).W_N^{-nk};\quad n = 0,1,….,N−1$
Note- Le calcul de la DFT peut être effectué avec une multiplication complexe N 2 et une addition complexe N (N-1).
$x_N = \begin{bmatrix}x(0)\\x(1)\\.\\.\\x(N-1) \end{bmatrix}\quad N\quad point\quad vector\quad of\quad signal\quad x_N$
$X_N = \begin{bmatrix}X(0)\\X(1)\\.\\.\\X(N-1) \end{bmatrix}\quad N\quad point\quad vector\quad of\quad signal\quad X_N$
$\begin{bmatrix}1 & 1 & 1 & ... & ... & 1\\1 & W_N & W_N^2 & ... & ... & W_N^{N-1}\\. & W_N^2 & W_N^4 & ... & ... & W_N^{2(N-1)}\\.\\1 & W_N^{N-1} & W_N^{2(N-1)} & ... & ... & W_N^{(N-1)(N-1)} \end{bmatrix}$
N - point DFT en terme de matrice est donné par - $X_N = W_Nx_N$
$W_N\longmapsto$ Matrice de transformation linéaire
$Now,\quad x_N = W_N^{-1}X_N$
IDFT sous forme de matrice est donné par
$$x_N = \frac{1}{N}W_N^*X_N$$En comparant les deux expressions de $x_N,\quad W_N^{-1} = \frac{1}{N}W_N^*$ et $W_N\times W_N^* = N[I]_{N\times N}$
Par conséquent, $W_N$ est une matrice de transformation linéaire, une matrice orthogonale (unitaire).
De la propriété périodique de $W_N$ et de sa propriété symétrique, on peut conclure que, $W_N^{k+N/2} = -W_N^k$
Symétrie circulaire
DFT à N points de durée finie x (n) de longueur N≤L, équivaut à la DFT à N points d'extension périodique de x (n), soit $x_p(n)$ de la période N. et $x_p(n) = \sum_{l = -\infty}^\infty x(n-Nl)$. Maintenant, si nous décalons la séquence, qui est une séquence périodique de k unités vers la droite, une autre séquence périodique est obtenue. Ceci est connu sous le nom de décalage circulaire et cela est donné par,
$$x_p^\prime (n) = x_p(n-k) = \sum_{l = -\infty}^\infty x(n-k-Nl)$$La nouvelle séquence finie peut être représentée comme
$$x_p^\prime (n) = \begin{cases}x_p^\prime(n), & 0\leq n\leq N-1\\0 & Otherwise\end{cases}$$Example - Soit x (n) = {1,2,4,3}, N = 4,
$x_p^\prime (n) = x(n-k,modulo\quad N)\equiv x((n-k))_N\quad;ex-if\quad k=2i.e\quad 2\quad unit\quad right\quad shift\quad and\quad N = 4,$
Sens horaire supposé comme direction positive.
Nous avons, $x\prime(n) = x((n-2))_4$
$x\prime(0) = x((-2))_4 = x(2) = 4$
$x\prime(1) = x((-1))_4 = x(3) = 3$
$x\prime(2) = x((-2))_4 = x(0) = 1$
$x\prime(3) = x((1))_4 = x(1) = 2$
Conclusion - Le décalage circulaire d'une séquence à N points équivaut à un décalage linéaire de son extension périodique et vice versa.
Séquence circulaire régulière - $x(N-n) = x(n),\quad 1\leq n\leq N-1$
$i.e.x_p(n) = x_p(-n) = x_p(N-n)$
Conjuguer même -$x_p(n) = x_p^*(N-n)$
Séquence circulaire étrange - $x(N-n) = -x(n),\quad 1\leq n\leq N-1$
$i.e.x_p(n) = -x_p(-n) = -x_p(N-n)$
Conjuguer impair - $x_p(n) = -x_p^*(N-n)$
Maintenant, $x_p(n) = x_{pe}+x_{po}(n)$, où,
$x_{pe}(n) = \frac{1}{2}[x_p(n)+x_p^*(N-n)]$
$x_{po}(n) = \frac{1}{2}[x_p(n)-x_p^*(N-n)]$
Pour tout signal réel x (n),$X(k) = X^*(N-k)$
$X_R(k) = X_R(N-k)$
$X_l(k) = -X_l(N-k)$
$\angle X(k) = -\angle X(N-K)$
Time reversal- inversion de l'échantillon autour du 0 ème échantillon. Ceci est donné comme;
$x((-n))_N = x(N-n),\quad 0\leq n\leq N-1$
L'inversion temporelle consiste à tracer des échantillons de séquence, dans le sens des aiguilles d'une montre, c'est-à-dire dans le sens négatif supposé.
Quelques autres propriétés importantes
Autres propriétés IDFT importantes $x(n)\longleftrightarrow X(k)$
Time reversal - $x((-n))_N = x(N-n)\longleftrightarrow X((-k))_N = X(N-k)$
Circular time shift - $x((n-l))_N \longleftrightarrow X(k)e^{j2\pi lk/N}$
Circular frequency shift - $x(n)e^{j2\pi ln/N} \longleftrightarrow X((k-l))_N$
Complex conjugate properties -
$x^*(n)\longleftrightarrow X^*((-k))_N = X^*(N-k)\quad and$
$x^*((-n))_N = x^*(N-n)\longleftrightarrow X^*(-k)$
Multiplication of two sequence -
$x_1(n)\longleftrightarrow X_1(k)\quad and\quad x_2(n)\longleftrightarrow X_2(k)$
$\therefore x_1(n)x_2(n)\longleftrightarrow X_1(k)\quadⓃ X_2(k)$
Circular convolution - et multiplication de deux DFT
$x_1(k)\quad Ⓝ x_2(k) =\sum_{k = 0}^{N-1}x_1(n).x_2((m-n))_n,\quad m = 0,1,2,... .,N-1 $
$x_1(k)\quad Ⓝ x_2(k)\longleftrightarrow X_1(k).X_2(k)$
Circular correlation - Si $x(n)\longleftrightarrow X(k)$ et $y(n)\longleftrightarrow Y(k)$ , alors il existe une séquence de corrélation croisée notée $\bar Y_{xy}$ tel que $\bar Y_{xy}(l) = \sum_{n = 0}^{N-1}x(n)y^*((n-l))_N = X(k).Y^*(k)$
Parseval’s Theorem - Si $x(n)\longleftrightarrow X(k)$ et $y(n)\longleftrightarrow Y(k)$;
$\displaystyle\sum\limits_{n = 0}^{N-1}x(n)y^*(n) = \frac{1}{N}\displaystyle\sum\limits_{n =0}^{N-1}X(k).Y^*(k)$
Prenons deux séquences de durée finie x 1 (n) et x 2 (n), de longueur entière égale à N. Leurs DFT sont respectivement X 1 (K) et X 2 (K), ce qui est montré ci-dessous -
$$X_1(K) = \sum_{n = 0}^{N-1}x_1(n)e^{\frac{j2\Pi kn}{N}}\quad k = 0,1,2...N-1$$ $$X_2(K) = \sum_{n = 0}^{N-1}x_2(n)e^{\frac{j2\Pi kn}{N}}\quad k = 0,1,2...N-1$$Maintenant, nous allons essayer de trouver la DFT d'une autre séquence x 3 (n), qui est donnée par X 3 (K)
$X_3(K) = X_1(K)\times X_2(K)$
En prenant l'IDFT de ce qui précède, nous obtenons
$x_3(n) = \frac{1}{N}\displaystyle\sum\limits_{n = 0}^{N-1}X_3(K)e^{\frac{j2\Pi kn}{N}}$
Après avoir résolu l'équation ci-dessus, enfin, nous obtenons
$x_3(n) = \displaystyle\sum\limits_{m = 0}^{N-1}x_1(m)x_2[((n-m))_N]\quad m = 0,1,2...N-1$
| Points de comparaison | Convolution linéaire | Convolution circulaire |
|---|---|---|
| Déplacement | Déplacement linéaire | Déplacement circulaire |
| Échantillons dans le résultat de la convolution | $N_1+N_2−1$ | $Max(N_1,N_2)$ |
| Trouver la réponse d'un filtre | Possible | Possible avec zéro rembourrage |
Méthodes de convolution circulaire
En règle générale, il existe deux méthodes adoptées pour effectuer une convolution circulaire et elles sont -
- Méthode du cercle concentrique,
- Méthode de multiplication matricielle.
Méthode du cercle concentrique
Laisser $x_1(n)$ et $x_2(n)$être deux séquences données. Les étapes suivies pour la convolution circulaire de$x_1(n)$ et $x_2(n)$ sont
Prenez deux cercles concentriques. Tracer N échantillons de$x_1(n)$ sur la circonférence du cercle extérieur (en maintenant les points successifs à égale distance) dans le sens anti-horaire.
Pour tracer $x_2(n)$, tracez N échantillons de $x_2(n)$dans le sens des aiguilles d'une montre sur le cercle intérieur, échantillon de départ placé au même point que le 0 ème échantillon de$x_1(n)$
Multipliez les échantillons correspondants sur les deux cercles et ajoutez-les pour obtenir la sortie.
Faites pivoter le cercle intérieur dans le sens inverse des aiguilles d'une montre avec un échantillon à la fois.
Méthode de multiplication matricielle
La méthode matricielle représente les deux séquences données $x_1(n)$ et $x_2(n)$ sous forme matricielle.
L'une des séquences données est répétée par décalage circulaire d'un échantillon à la fois pour former une matrice NXN.
L'autre séquence est représentée sous forme de matrice de colonnes.
La multiplication de deux matrices donne le résultat d'une convolution circulaire.
DFT fournit une approche alternative à la convolution dans le domaine temporel. Il peut être utilisé pour effectuer un filtrage linéaire dans le domaine fréquentiel.
Donc,$Y(\omega) = X(\omega).H(\omega)\longleftrightarrow y(n)$.
Le problème dans cette approche du domaine fréquentiel est que $Y(\omega)$, $X(\omega)$ et $H(\omega)$sont une fonction continue de ω, ce qui n'est pas fructueux pour le calcul numérique sur les ordinateurs. Cependant, DFT fournit une version échantillonnée de ces formes d'onde pour résoudre le problème.
L'avantage est que, ayant une connaissance des techniques DFT plus rapides comme la FFT, un algorithme plus efficace du point de vue calcul peut être développé pour le calcul informatique numérique par rapport à l'approche du domaine temporel.
Considérons une séquence de durée finie, $[x(n) = 0,\quad for,n<0\quad and\quad n\geq L]$ (équation généralisée), excite un filtre linéaire avec réponse impulsionnelle $[h(n) = 0,\quad forn<0\quad and\quad n\geq M]$.
$$x(n)y(n)$$ $$output = y(n) = \sum_{k = 0}^{M-1}h(k).x(n-k)$$D'après l'analyse de convolution, il est clair que la durée de y (n) est L + M − 1.
Dans le domaine fréquentiel,
$$Y(\omega) = X(\omega).H(\omega)$$Maintenant, $Y(\omega)$ est une fonction continue de ω et il est échantillonné à un ensemble de fréquences discrètes avec un nombre d'échantillons distincts qui doit être égal ou supérieur $L+M-1$.
$$DFT\quad size = N\geq L+M-1$$Avec $\omega = \frac{2\pi}{N}k$,
$Y(\omega) = X(k).H(k)$, où k = 0,1,…., N-1
Où, X (k) et H (k) sont des DFT à N points de x (n) et h (n) respectivement. $x(n)\& h(n)$ sont remplis de zéros jusqu'à la longueur N. Cela ne déformera pas les spectres continus $X(\omega)$ et $H(\omega)$. Depuis$N\geq L+M-1$, La DFT à N points de la séquence de sortie y (n) est suffisante pour représenter y (n) dans le domaine fréquentiel et ces faits impliquent que la multiplication des DFT à N points de X (k) et H (k), suivie du calcul de l'IDFT à N points doit donner y (n).
Cela implique une convolution circulaire à N points de x (n) et H (n) avec un remplissage nul, égale à la convolution linéaire de x (n) et h (n).
Ainsi, DFT peut être utilisé pour le filtrage linéaire.
Caution - N doit toujours être supérieur ou égal à $L+M-1$. Sinon, l'effet d'alias endommagerait la séquence de sortie.
Supposons que la séquence d'entrée x (n) de longue durée doit être traitée avec un système ayant une réponse impulsionnelle de durée finie en convoluant les deux séquences. Puisque le filtrage linéaire effectué via DFT implique une opération sur un bloc de données de taille fixe, la séquence d'entrée est divisée en différents blocs de données de taille fixe avant le traitement.
Les blocs successifs sont ensuite traités un par un et les résultats sont combinés pour produire le résultat net.
Comme la convolution est effectuée en divisant la longue séquence d'entrée en différentes sections de taille fixe, elle est appelée convolution sectionnée. Une longue séquence d'entrée est segmentée en blocs de taille fixe, avant le traitement du filtre FIR.
Deux méthodes sont utilisées pour évaluer la convolution discrète -
Overlap-save method
Overlap-add method
Méthode d'enregistrement par chevauchement
Overlap – save est le nom traditionnel d'un moyen efficace d'évaluer la convolution discrète entre un signal très long x (n) et un filtre à réponse impulsionnelle finie (FIR) h (n). Vous trouverez ci-dessous les étapes de la méthode de sauvegarde par chevauchement -
Soit la longueur du bloc de données d'entrée = N = L + M-1. Par conséquent, la longueur DFT et IDFT = N. Chaque bloc de données porte M-1 points de données du bloc précédent suivis de L nouveaux points de données pour former une séquence de données de longueur N = L + M-1.
Tout d'abord, la DFT à N points est calculée pour chaque bloc de données.
En ajoutant des zéros (L-1), la réponse impulsionnelle du filtre FIR est augmentée en longueur et N point DFT est calculé et stocké.
Multiplication de deux DFT à N points H (k) et X m (k): Y ′ m (k) = H (k) .X m (k), où K = 0,1,2,… N-1
Alors, IDFT [Y ′ m ((k)] = y ′ ((n) = [y ′ m (0), y ′ m (1), y ′ m (2), ....... y) ' m (m-1), y' m (m), ....... y ' m (N-1)]
(ici, N-1 = L + M-2)
Les premiers points M-1 sont corrompus en raison de l'aliasing et, par conséquent, ils sont supprimés car l'enregistrement de données est de longueur N.
Les derniers points L sont exactement les mêmes en raison de la convolution, donc
y ′ m (n) = y m (n) où n = M, M + 1,… .N-1
Pour éviter le crénelage, les derniers éléments M-1 de chaque enregistrement de données sont sauvegardés et ces points sont reportés à l'enregistrement suivant et deviennent les 1 er éléments M-1.

Le résultat de l'IDFT, où les premiers M-1 points sont évités, pour annuler l'aliasing et les L points restants constituent le résultat souhaité comme celui d'une convolution linéaire.
Overlap Add, méthode
Vous trouverez ci-dessous les étapes pour connaître la convolution discrète en utilisant la méthode Overlap -
Soit la taille du bloc de données d'entrée L. Par conséquent, la taille de DFT et IDFT: N = L + M-1
Chaque bloc de données est ajouté avec M-1 zéros au dernier.
Calculez la DFT à N points.

Deux DFT à N points sont multipliés: Y m (k) = H (k) .X m (k), où k = 0 ,, 1,2,…., N-1
IDFT [Y m (k)] produit des blocs de longueur N qui ne sont pas affectés par l'aliasing car la taille de DFT est N = L + M-1 et augmente les longueurs des séquences à N points en ajoutant M-1 zéros à chacun bloquer.
Les derniers points M-1 de chaque bloc doivent être superposés et ajoutés aux premiers points M-1 du bloc suivant.
(raison: chaque bloc de données se termine par M-1 zéros)
Par conséquent, cette méthode est connue comme méthode Overlap-add. Ainsi, nous obtenons -
y (n) = {y 1 (0), y 1 (1), y 1 (2), ... .., y 1 (L-1), y 1 (L) + y 2 (0), y 1 (L + 1) + y 2 (1), ... ... .., y 1 (N-1) + y 2 (M-1), y 2 (M), ... .. . ... ... ...}
DCT (Discrete Cosine Transform) est une séquence à N entrées x (n), 0≤n≤N-1, sous forme de transformation linéaire ou de combinaison d'exponentielles complexes. De ce fait, les coefficients DFT sont en général complexes même si x (n) est réel.
Supposons que nous essayons de trouver une transformation orthogonale qui a une structure N × N qui exprime une séquence réelle x (n) comme une combinaison linéaire de séquence cosinus. Nous savons déjà que -
$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)cos\frac{2\Pi kn}{N}0\leq k \leq N-1$
Et $x(n) = \frac{1}{N}\sum_{k = 0}^{N-1}x(k)cos\frac{2\Pi kn}{N}0\leq k \leq N-1$
Ceci est possible si la séquence de N points x (n) est réelle et paire. Donc,$x(n) = x(N-n),0\leq n \leq (N-1)$. Le DFT qui en résulte est réel et uniforme. Ces choses montrent clairement que nous pourrions éventuellement réaliser une transformée en cosinus discrète, pour toute séquence réelle à N points en prenant le 2N point DFT d'une «extension paire» de séquence.
DCT est, fondamentalement, utilisé dans le traitement d'image et de parole. Il est également utilisé pour la compression d'images et de signaux vocaux.
$DFT[s(n)] = S(k) = \sum_{n = 0}^{2N-1}s(n)W_{2N}^{nk},\quad where\quad 0\leq k \leq 2N-1$
$S(k) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)W_{2N}^{nk}+\displaystyle\sum\limits_{n = N}^{2N-1}x(2N-n-1)W_{2N}^{nk};\quad where\quad 0\leq k\leq 2N-1$
$\Rightarrow S(k) = W_{2N}^{-k/2}+\sum_{n = 0}^{N-1}x(n) [W_{2N}^{nk}W_{2N}^{k/2}+W_{2N}^{-nk}W_{2N}^{-k/2}];\quad where\quad 0\leq k\leq 2N-1$
$\Rightarrow S(k) = W_{2N}^{\frac{k}{2}}\sum_{n = 0}^{N-1}x(n)\cos [\frac{\pi}{N}(n+\frac{1}{2})k];\quad where\quad 0\leq k\leq 2N-1$
DCT est défini par,
$V(k) = 2\sum_{n = 0}^{N-1}x(n)\cos [\frac{\pi}{2}(n+\frac{1}{2})k]\quad where\quad 0\leq k\leq N-1$
$\Rightarrow V(k) = W_{2N}^{\frac{k}{2}}S(k)\quad or\quad S(k) = W_{2N}^{\frac{k}{2}}V(k),\quad where\quad 0\leq k\leq N-1$
$\Rightarrow V(k) = 2R[W_{2N}^{\frac{k}{2}}\sum_{n = 0}^{N-1}x(n)W_{2N}^{nk}],\quad where\quad 0\leq k\leq N-1$
Exemple 1
Vérifiez le théorème de Parseval de la séquence $x(n) = \frac{1^n}{4}u(n)$
Solution - $\displaystyle\sum\limits_{-\infty}^\infty|x_1(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X_1(e^{j\omega})|^2d\omega$
LHS $\displaystyle\sum\limits_{-\infty}^\infty|x_1(n)|^2$
$= \displaystyle\sum\limits_{-\infty}^{\infty}x(n)x^*(n)$
$= \displaystyle\sum\limits_{-\infty}^\infty(\frac{1}{4})^{2n}u(n) = \frac{1}{1-\frac{1}{16}} = \frac{16}{15}$
RHS $X(e^{j\omega}) = \frac{1}{1-\frac{1}{4}e-j\omega} = \frac{1}{1-0.25\cos \omega+j0.25\sin \omega}$
$\Longleftrightarrow X^*(e^{j\omega}) = \frac{1}{1-0.25\cos \omega-j0.25\sin \omega}$
Calculateur, $X(e^{j\omega}).X^*(e^{j\omega})$
$= \frac{1}{(1-0.25\cos \omega)^2+(0.25\sin \omega)^2} = \frac{1}{1.0625-0.5\cos \omega}$
$\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{1}{1.0625-0.5\cos \omega}d\omega$
$\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{1}{1.0625-0.5\cos \omega}d\omega = 16/15$
Nous pouvons voir que, LHS = RHS. (Par conséquent prouvé)
Exemple 2
Calculez la DFT à N points de $x(n) = 3\delta (n)$
Solution - Nous savons que,
$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{\frac{j2\Pi kn}{N}}$
$= \displaystyle\sum\limits_{n = 0}^{N-1}3\delta(n)e^{\frac{j2\Pi kn}{N}}$
$ = 3\delta (0)\times e^0 = 1$
Alors,$x(k) = 3,0\leq k\leq N-1$… Ans.
Exemple 3
Calculez la DFT à N points de $x(n) = 7(n-n_0)$
Solution - Nous savons que,
$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{\frac{j2\Pi kn}{N}}$
En substituant la valeur de x (n),
$\displaystyle\sum\limits_{n = 0}^{N-1}7\delta (n-n_0)e^{-\frac{j2\Pi kn}{N}}$
$= e^{-kj14\Pi kn_0/N}$… Ans
Dans les méthodes DFT précédentes, nous avons vu que la partie calcul est trop longue. Nous voulons réduire cela. Cela peut être fait via FFT ou transformée de Fourier rapide. Ainsi, nous pouvons dire que la FFT n'est rien d'autre que le calcul d'une transformée de Fourier discrète dans un format algorithmique, où la partie de calcul sera réduite.
Le principal avantage d'avoir FFT est que grâce à elle, nous pouvons concevoir les filtres FIR. Mathématiquement, la FFT peut être écrite comme suit;
$$x[K] = \displaystyle\sum\limits_{n = 0}^{N-1}x[n]W_N^{nk}$$Prenons un exemple pour mieux le comprendre. Nous avons considéré huit points nommés à partir de$x_0\quad to\quad x_7$. Nous choisirons les termes pairs dans un groupe et les termes impairs dans l'autre. Une vue schématique de ce qui précède a été montrée ci-dessous -
Ici, les points x 0 , x 2 , x 4 et x 6 ont été regroupés dans une catégorie et de même, les points x 1 , x 3 , x 5 et x 7 ont été placés dans une autre catégorie. Maintenant, nous pouvons en outre les faire par groupe de deux et procéder au calcul. Voyons maintenant comment ces deux autres aident au calcul.
$x[k] = \displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r]W_N^{2rk}+\displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_N^{(2r+1)k}$
$= \sum_{r = 0}^{\frac{N}{2}-1}x[2r]W_{N/2}^{rk}+\sum_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_{N/2}^{rk}\times W_N^k$
$= G[k]+H[k]\times W_N^k$
Au départ, nous avons pris une séquence de huit points, mais plus tard, nous avons divisé celle-là en deux parties G [k] et H [k]. G [k] représente la partie paire tandis que H [k] représente la partie impaire. Si nous voulons le réaliser à travers un diagramme, alors cela peut être montré comme ci-dessous -
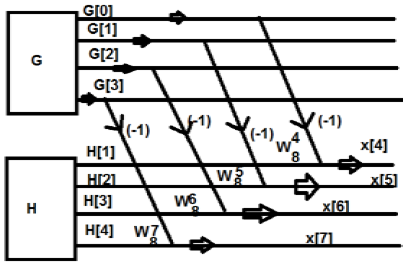
À partir de la figure ci-dessus, nous pouvons voir que
$W_8^4 = -1$
$W_8^5 = -W_8^1$
$W_8^6 = -W_8^2$
$W_8^7 = -W_8^3$
De même, les valeurs finales peuvent être écrites comme suit -
$G[0]-H[0] = x[4]$
$G[1]-W_8^1H[1] = x[5]$
$G[2]-W_8^2H[2] = x[6]$
$G[1]-W_8^3H[3] = x[7]$
Celui ci-dessus est une série périodique. L'inconvénient de ce système est que K ne peut pas être cassé au-delà de 4 points. Maintenant, décomposons ce qui précède en plus. Nous obtiendrons les structures quelque chose comme ça
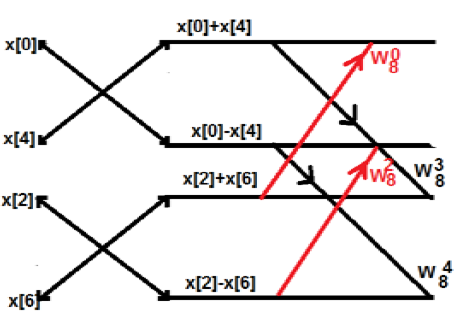
Exemple
Considérons la séquence x [n] = {2,1, -1, -3,0,1,2,1}. Calculez la FFT.
Solution - La séquence donnée est x [n] = {2,1, -1, -3,0,1,2,1}
Disposez les termes comme indiqué ci-dessous;
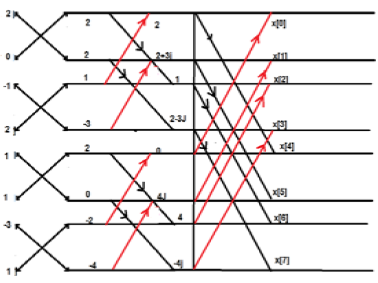
Cette utilisation efficace de la mémoire est importante pour concevoir un matériel rapide pour calculer la FFT. Le terme calcul sur place est utilisé pour décrire cette utilisation de la mémoire.
Décimation en séquence temporelle
Dans cette structure, nous représentons tous les points au format binaire c'est-à-dire en 0 et 1. Ensuite, nous inversons ces structures. La séquence que nous obtenons après cela est connue sous le nom de séquence d'inversion de bits. Ceci est également connu sous le nom de décimation en séquence temporelle. Le calcul sur place d'une DFT à huit points est présenté dans un format tabulaire comme indiqué ci-dessous -
| POINTS | FORMAT BINAIRE | RENVERSEMENT | POINTS ÉQUIVALENTS |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| sept | 111 | 111 | sept |
Décimation dans la séquence de fréquences
Outre la séquence temporelle, une séquence à N points peut également être représentée en fréquence. Prenons une séquence en quatre points pour mieux le comprendre.
Que la séquence soit $x[0], x[1], x[2], x[3], x[4], x[5], x[6], x[7]$. Nous allons regrouper deux points en un seul groupe, dans un premier temps. Mathématiquement, cette séquence peut être écrite comme;
$$x[k] = \sum_{n = 0}^{N-1}x[n]W_N^{n-k}$$Maintenant, faisons un groupe de numéro de séquence 0 à 3 et un autre groupe de séquence 4 à 7. Maintenant, mathématiquement, cela peut être représenté par;
$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[n]W_N^{nk}+\displaystyle\sum\limits_{n = N/2}^{N-1}x[n]W_N^{nk}$$Remplaçons n par r, où r = 0, 1, 2… (N / 2-1). Mathématiquement,
$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[r]W_{N/2}^{nr}$$Nous prenons les quatre premiers points (x [0], x [1], x [2], x [3]) au départ, et essayons de les représenter mathématiquement comme suit -
$\sum_{n = 0}^3x[n]W_8^{nk}+\sum_{n = 0}^3x[n+4]W_8^{(n+4)k}$
$= \lbrace \sum_{n = 0}^3x[n]+\sum_{n = 0}^3x[n+4]W_8^{(4)k}\rbrace \times W_8^{nk}$
maintenant $X[0] = \sum_{n = 0}^3(X[n]+X[n+4])$
$X[1] = \sum_{n = 0}^3(X[n]+X[n+4])W_8^{nk}$
$= [X[0]-X[4]+(X[1]-X[5])W_8^1+(X[2]-X[6])W_8^2+(X[3]-X[7])W_8^3$
Nous pouvons encore le diviser en deux autres parties, ce qui signifie qu'au lieu de les diviser en séquence à 4 points, nous pouvons les diviser en séquence à 2 points.
Les filtres FIR peuvent être utiles pour la conception assistée par ordinateur des filtres. Prenons un exemple et voyons comment cela fonctionne. Ci-dessous est une figure du filtre souhaité.

Lors de la conception par ordinateur, nous divisons l'ensemble des figures du graphe continu en valeurs discrètes. Dans certaines limites, nous le décomposons en un nombre de 64, 256 ou 512 (et ainsi de suite) de parties ayant des grandeurs discrètes.
Dans l'exemple ci-dessus, nous avons pris des limites entre -π et + π. Nous l'avons divisé en 256 parties. Les points peuvent être représentés par H (0), H (1),… jusqu'à H (256). Ici, nous appliquons l'algorithme IDFT et cela nous donnera des caractéristiques de phase linéaire.
Parfois, nous pouvons être intéressés par un ordre particulier de filtre. Disons que nous voulons réaliser ce qui précède la conception donnée à 9 e filtre d'ordre. Donc, nous prenons les valeurs de filtre comme h0, h1, h2… .h9. Mathématiquement, il peut être montré comme ci-dessous
$$H(e^{j\omega}) = h_0+h_1e^{-j\omega}+h_2e^{-2j\omega}+.....+h_9e^{-9j\omega}$$Là où il y a un grand nombre de luxations, on prend le maximum de points.
Par exemple, dans la figure ci-dessus, il y a une baisse soudaine de la pente entre les points B et C. Donc, nous essayons de prendre des valeurs plus discrètes à ce point, mais il y a une pente constante entre les points C et D. moins de nombre de valeurs discrètes.
Pour concevoir le filtre ci-dessus, nous suivons le processus de minimisation comme suit;
$H(e^{j\omega1}) = h_0+h_1e^{-j\omega1}+h_2e^{-2j\omega1}+.....+h_9e^{-9j\omega1}$
$H(e^{j\omega2}) = h_0+h_1e^{-j\omega2}+h_2e^{-2j\omega2}+.....+h_9e^{-9j\omega2}$
De même,
$(e^{j\omega1000}) = h_0+h_1eH^{-j\omega1000}h_2e^{-2j\omega1000}+.....+h_9+e^{-9j\omega1000}$
Représentant l'équation ci-dessus sous forme matricielle, nous avons -
$$\begin{bmatrix}H(e^{j\omega_1})\\.\\.\\H(e^{j\omega_{1000}}) \end{bmatrix} = \begin{bmatrix}e^{-j\omega_1} & ... & e^{-j9\omega_1} \\. & & . \\. & & . \\e^{-j\omega_{1000}} &... & e^{j9\omega_{1000}} \end{bmatrix}\begin{bmatrix}h_0\\.\\.\\h_9\end{bmatrix}$$Prenons la matrice 1000 × 1 comme B, la matrice 1000 × 9 comme A et la matrice 9 × 1 comme $\hat{h}$.
Donc, pour résoudre la matrice ci-dessus, nous écrirons
$\hat{h} = [A^TA]^{-1}A^{T}B$
$= [A^{*T}A]^{-1}A^{*T}B$
où A * représente le conjugué complexe de la matrice A.