DSP - Opérations sur le décalage des signaux
Le décalage signifie le mouvement du signal, soit dans le domaine temporel (autour de l'axe Y) soit dans le domaine d'amplitude (autour de l'axe X). En conséquence, nous pouvons classer le décalage en deux catégories nommées Décalage temporel et Décalage d'amplitude, celles-ci sont décrites ci-dessous.
Changement de temps
Le décalage temporel signifie le décalage des signaux dans le domaine temporel. Mathématiquement, il peut être écrit comme
$$ x (t) \ flèche droite y (t + k) $$Cette valeur K peut être positive ou négative. Selon le signe de la valeur k, nous avons deux types de décalage nommés décalage à droite et décalage à gauche.
Cas 1 (K> 0)
Lorsque K est supérieur à zéro, le décalage du signal a lieu vers «gauche» dans le domaine temporel. Par conséquent, ce type de décalage est appelé décalage à gauche du signal.
Example
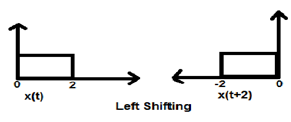
Cas 2 (K <0)
Lorsque K est inférieur à zéro, le décalage du signal a lieu vers la droite dans le domaine temporel. Par conséquent, ce type de décalage est connu sous le nom de décalage à droite.
Example
La figure ci-dessous montre le décalage vers la droite d'un signal de 2.
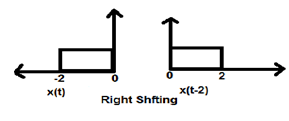
Décalage d'amplitude
Le décalage d'amplitude signifie le décalage du signal dans le domaine d'amplitude (autour de l'axe X). Mathématiquement, il peut être représenté par -
$$ x (t) \ flèche droite x (t) + K $$Cette valeur K peut être positive ou négative. En conséquence, nous avons deux types de décalage d'amplitude qui sont ensuite discutés ci-dessous.
Cas 1 (K> 0)
Lorsque K est supérieur à zéro, le décalage du signal a lieu vers le haut sur l'axe des x. Par conséquent, ce type de décalage est appelé déplacement vers le haut.
Example
Considérons un signal x (t) qui est donné comme;
$$ x = \ begin {cases} 0, & t <0 \\ 1, & 0 \ leq t \ leq 2 \\ 0, & t> 0 \ end {cases} $$Supposons que nous ayons pris K = + 1 pour que le nouveau signal puisse s'écrire -
$ y (t) \ rightarrow x (t) + 1 $ Donc, y (t) peut finalement être écrit comme;
$$ x (t) = \ begin {cases} 1, & t <0 \\ 2, & 0 \ leq t \ leq 2 \\ 1, & t> 0 \ end {cases} $$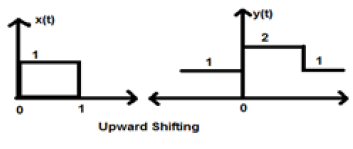
Cas 2 (K <0)
Lorsque K est inférieur à zéro, le décalage du signal a lieu vers le bas sur l'axe X. Par conséquent, on parle de décalage vers le bas du signal.
Example
Considérons un signal x (t) qui est donné comme;
$$ x (t) = \ begin {cases} 0, & t <0 \\ 1, & 0 \ leq t \ leq 2 \\ 0, & t> 0 \ end {cases} $$Supposons que nous ayons pris K = -1 pour que le nouveau signal puisse s'écrire;
$ y (t) \ rightarrow x (t) -1 $ Donc, y (t) peut finalement être écrit comme;
$$ y (t) = \ begin {cases} -1, & t <0 \\ 0, & 0 \ leq t \ leq 2 \\ -1, & t> 0 \ end {cases} $$