DSP - Calcul sur place
Cette utilisation efficace de la mémoire est importante pour concevoir un matériel rapide pour calculer la FFT. Le terme calcul sur place est utilisé pour décrire cette utilisation de la mémoire.
Décimation en séquence temporelle
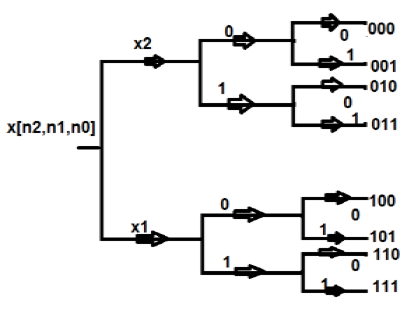
Dans cette structure, nous représentons tous les points au format binaire c'est-à-dire en 0 et 1. Ensuite, nous inversons ces structures. La séquence que nous obtenons après cela est connue sous le nom de séquence d'inversion de bits. Ceci est également connu sous le nom de décimation en séquence temporelle. Le calcul sur place d'une DFT à huit points est présenté dans un format tabulaire comme indiqué ci-dessous -
| POINTS | FORMAT BINAIRE | RENVERSEMENT | POINTS ÉQUIVALENTS |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| sept | 111 | 111 | sept |
Décimation dans la séquence de fréquences
Outre la séquence temporelle, une séquence à N points peut également être représentée en fréquence. Prenons une séquence de quatre points pour mieux le comprendre.
Soit la séquence $ x [0], x [1], x [2], x [3], x [4], x [5], x [6], x [7] $. Nous allons regrouper deux points en un seul groupe, dans un premier temps. Mathématiquement, cette séquence peut être écrite comme;
$$ x [k] = \ sum_ {n = 0} ^ {N-1} x [n] W_N ^ {nk} $$Maintenant, faisons un groupe de numéro de séquence 0 à 3 et un autre groupe de séquence 4 à 7. Maintenant, mathématiquement, cela peut être représenté par;
$$ \ displaystyle \ sum \ limits_ {n = 0} ^ {\ frac {N} {2} -1} x [n] W_N ^ {nk} + \ displaystyle \ sum \ limits_ {n = N / 2} ^ {N-1} x [n] W_N ^ {nk} $$Remplaçons n par r, où r = 0, 1, 2… (N / 2-1). Mathématiquement,
$$ \ displaystyle \ sum \ limits_ {n = 0} ^ {\ frac {N} {2} -1} x [r] W_ {N / 2} ^ {nr} $$Nous prenons les quatre premiers points (x [0], x [1], x [2], x [3]) au départ, et essayons de les représenter mathématiquement comme suit -
$ \ sum_ {n = 0} ^ 3x [n] W_8 ^ {nk} + \ sum_ {n = 0} ^ 3x [n + 4] W_8 ^ {(n + 4) k} $
$ = \ lbrace \ sum_ {n = 0} ^ 3x [n] + \ sum_ {n = 0} ^ 3x [n + 4] W_8 ^ {(4) k} \ rbrace \ times W_8 ^ {nk} $
maintenant $ X [0] = \ sum_ {n = 0} ^ 3 (X [n] + X [n + 4]) $
$ X [1] = \ sum_ {n = 0} ^ 3 (X [n] + X [n + 4]) W_8 ^ {nk} $
$ = [X [0] -X [4] + (X [1] -X [5]) W_8 ^ 1 + (X [2] -X [6]) W_8 ^ 2 + (X [3] -X [7]) W_8 ^ 3 $
Nous pouvons encore le diviser en deux autres parties, ce qui signifie qu'au lieu de les diviser en séquence à 4 points, nous pouvons les diviser en séquence à 2 points.