DSP - Opérations sur la mise à l'échelle des signaux
Mise à l'échelle d'un signal signifie, une constante est multipliée par le temps ou l'amplitude du signal.
Mise à l'échelle du temps
Si une constante est multipliée sur l'axe des temps, on parle alors de mise à l'échelle du temps. Cela peut être représenté mathématiquement par;
$ x (t) \ rightarrow y (t) = x (\ alpha t) $ ou $ x (\ frac {t} {\ alpha}) $; où α ≠ 0
Ainsi, l'axe des y étant le même, la grandeur de l'axe des x diminue ou augmente selon le signe de la constante (qu'elle soit positive ou négative). Par conséquent, la mise à l'échelle peut également être divisée en deux catégories, comme indiqué ci-dessous.
Compression du temps
Chaque fois que alpha est supérieur à zéro, l'amplitude du signal est divisée par alpha tandis que la valeur de l'axe Y reste la même. Ceci est connu sous le nom de compression temporelle.
Example
Considérons un signal x (t), qui est représenté comme dans la figure ci-dessous. Prenons la valeur de alpha comme 2. Donc, y (t) sera x (2t), ce qui est illustré dans la figure donnée.

Clairement, nous pouvons voir sur les figures ci-dessus que la grandeur de temps en axe y reste la même mais l'amplitude en axe x diminue de 4 à 2. Il s'agit donc d'un cas de compression temporelle.
Expansion du temps
Lorsque le temps est divisé par l'alpha constant, l'amplitude de l'axe Y du signal est multipliée par alpha, en conservant l'amplitude de l'axe X telle qu'elle est. Par conséquent, cela s'appelle un signal de type à expansion temporelle.
Example
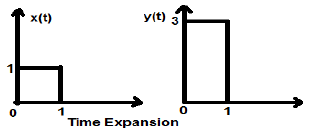
Considérons un signal carré x (t), de grandeur 1. Lorsque nous l'avons mis à l'échelle temporelle par une constante 3, tel que $ x (t) \ rightarrow y (t) \ rightarrow x (\ frac {t} {3} ) $, alors l'amplitude du signal est modifiée par 3 fois, comme illustré dans la figure ci-dessous.
Mise à l'échelle d'amplitude
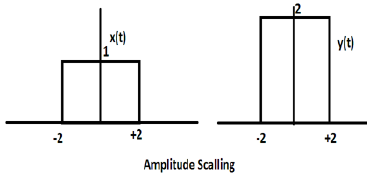
La multiplication d'une constante par l'amplitude du signal provoque une mise à l'échelle d'amplitude. En fonction du signe de la constante, il peut s'agir d'une échelle d'amplitude ou d'une atténuation. Considérons un signal carré x (t) = Π (t / 4).
Supposons que nous définissions une autre fonction y (t) = 2 Π (t / 4). Dans ce cas, la valeur de l'axe des y sera doublée, en conservant la valeur de l'axe des temps telle quelle. Le est illustré dans la figure ci-dessous.
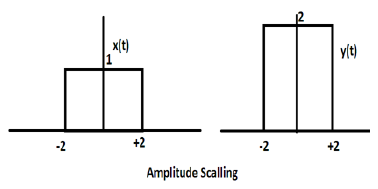
Considérons une autre fonction d'onde carrée définie comme z (t) où z (t) = 0,5 Π (t / 4). Ici, l'amplitude de la fonction z (t) sera la moitié de celle de x (t) c'est-à-dire que l'axe des temps reste le même, l'axe d'amplitude sera divisé par deux. Ceci est illustré par la figure ci-dessous.