DSP - Opérations sur la convolution des signaux
La convolution de deux signaux dans le domaine temporel équivaut à la multiplication de leur représentation dans le domaine fréquentiel. Mathématiquement, nous pouvons écrire la convolution de deux signaux comme
$$ y (t) = x_ {1} (t) * x_ {2} (t) $$ $$ = \ int _ {- \ infty} ^ {\ infty} x_ {1} (p) .x_ {2 } (tp) dp $$Étapes de la convolution
- Prenez le signal x 1 (t) et mettez t = p ici pour qu'il soit x 1 (p).
- Prenez le signal x 2 (t) et effectuez l'étape 1 et faites-le x 2 (p).
- Faites le pliage du signal soit x 2 (-p).
- Effectuez le décalage temporel du signal ci-dessus x 2 [- (pt)]
- Faites ensuite la multiplication des deux signaux. soit $ x_ {1} (p) .x_ {2} [- (p − t)] $
Exemple
Faisons la convolution d'un signal de pas u (t) avec son propre type.
$ y (t) = u (t) * u (t) $
$ = \ int _ {- \ infty} ^ {\ infty} [u (p) .u [- (pt)] dp $
Maintenant, ce t peut être supérieur ou inférieur à zéro, comme le montrent les figures ci-dessous
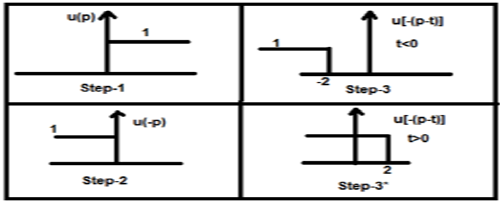
Ainsi, avec le cas ci-dessus, le résultat se présente avec les possibilités suivantes
$ y (t) = \ begin {cases} 0, & if \ quad t <0 \\\ int_ {0} ^ {t} 1dt, & pour \ quad t> 0 \ end {cases} $
$ = \ begin {cases} 0, & if \ quad t <0 \\ t, & t> 0 \ end {cases} = r (t) $
Propriétés de la convolution
Commutatif
Il déclare que l'ordre de convolution n'a pas d'importance, ce qui peut être montré mathématiquement comme
$$ x_ {1} (t) * x_ {2} (t) = x_ {2} (t) * x_ {1} (t) $$Associatif
Il déclare que l'ordre de convolution impliquant trois signaux peut être n'importe quoi. Mathématiquement, il peut être représenté par;
$$ x_ {1} (t) * [x_ {2} (t) * x_ {3} (t)] = [x_ {1} (t) * x_ {2} (t)] * x_ {3} (t) $$Distributif
Deux signaux peuvent être ajoutés en premier, puis leur convolution peut être faite au troisième signal. Cela équivaut à la convolution de deux signaux individuellement avec le troisième signal et ajouté finalement. Mathématiquement, cela peut s'écrire;
$$ x_ {1} (t) * [x_ {2} (t) + x_ {3} (t)] = [x_ {1} (t) * x_ {2} (t) + x_ {1} ( t) * x_ {3} (t)] $$Surface
Si un signal est le résultat de la convolution de deux signaux, alors la zone du signal est la multiplication de ces signaux individuels. Mathématiquement, cela peut être écrit
Si $ y (t) = x_ {1} * x_ {2} (t) $
Alors, Aire de y (t) = Aire de x 1 (t) X Aire de x 2 (t)
Mise à l'échelle
Si deux signaux sont mis à l'échelle à une constante inconnue «a» et qu'une convolution est effectuée, le signal résultant sera également convolué à la même constante «a» et sera divisé par cette quantité comme indiqué ci-dessous.
Si, $ x_ {1} (t) * x_ {2} (t) = y (t) $
Alors, $ x_ {1} (at) * x_ {2} (at) = \ frac {y (at)} {a}, a \ ne 0 $
Retard
Supposons qu'un signal y (t) est le résultat de la convolution de deux signaux x1 (t) et x2 (t). Si les deux signaux sont retardés respectivement du temps t1 et t2, alors le signal résultant y (t) sera retardé de (t1 + t2). Mathématiquement, il peut s'écrire -
Si, $ x_ {1} (t) * x_ {2} (t) = y (t) $
Alors, $ x_ {1} (t-t_ {1}) * x_ {2} (t-t_ {2}) = y [t- (t_ {1} + t_ {2})] $
Exemples résolus
Example 1 - Trouver la convolution des signaux u (t-1) et u (t-2).
Solution- Les signaux donnés sont u (t-1) et u (t-2). Leur convolution peut être effectuée comme indiqué ci-dessous -
$ y (t) = u (t-1) * u (t-2) $
$ y (t) = \ int _ {- \ infty} ^ {+ \ infty} [u (t-1) .u (t-2)] dt $
$ = r (t-1) + r (t-2) $
$ = r (t-3) $
Example 2 - Trouver la convolution de deux signaux donnée par
$x_{1}(n) = \lbrace 3,-2, 2\rbrace $
$ x_ {2} (n) = \ begin {cases} 2, & 0 \ leq n \ leq 4 \\ 0, & x> ailleurs \ end {cases} $
Solution -
x 2 (n) peut être décodé comme $ x_ {2} (n) = \ lbrace 2,2,2,2,2 \ rbrace Originalfirst $
x 1 (n) est précédemment donné $ = \ lbrace 3, -2,3 \ rbrace = 3-2Z ^ {- 1} + 2Z ^ {- 2} $
De même, $ x_ {2} (z) = 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {- 4} $
Signal résultant,
$ X (Z) = X_ {1} (Z) X_ {2} (z) $
$ = \ lbrace 3-2Z ^ {- 1} + 2Z ^ {- 2} \ rbrace \ times \ lbrace 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {-4} \ rbrace $
$ = 6 + 2Z ^ {- 1} + 6Z ^ {- 2} + 6Z ^ {- 3} + 6Z ^ {- 4} + 6Z ^ {- 5} $
En prenant la transformation Z inverse de ce qui précède, nous obtiendrons le signal résultant comme
$ x (n) = \ lbrace 6,2,6,6,6,0,4 \ rbrace $ Origin au premier
Example 3 - Déterminer la convolution des 2 signaux suivants -
$x(n) = \lbrace 2,1,0,1\rbrace$
$h(n) = \lbrace 1,2,3,1\rbrace$
Solution -
En prenant la transformation en Z des signaux, nous obtenons,
$ x (z) = 2 + 2Z ^ {- 1} + 2Z ^ {- 3} $
Et $ h (n) = 1 + 2Z ^ {- 1} + 3Z ^ {- 2} + Z ^ {- 3} $
Maintenant, la convolution de deux signaux signifie la multiplication de leurs transformations Z
Soit $ Y (Z) = X (Z) \ fois h (Z) $
$ = \ lbrace 2 + 2Z ^ {- 1} + 2Z ^ {- 3} \ rbrace \ times \ lbrace 1 + 2Z ^ {- 1} + 3Z ^ {- 2} + Z ^ {- 3} \ rbrace $
$ = \ lbrace 2 + 5Z ^ {- 1} + 8Z ^ {- 2} + 6Z ^ {- 3} + 3Z ^ {- 4} + 3Z ^ {- 5} + Z ^ {- 6} \ rbrace $
En prenant la transformation Z inverse, le signal résultant peut être écrit comme;
$ y (n) = \ lbrace 2,5,8,6,6,1 \ rbrace Originalfirst $