Traitement numérique du signal - Signaux CT de base

Pour tester un système, on utilise généralement des signaux standard ou de base. Ces signaux sont les éléments de base de nombreux signaux complexes. Par conséquent, ils jouent un rôle très important dans l'étude des signaux et des systèmes.

Fonction d'impulsion d'unité ou de delta

Un signal, qui satisfait la condition, $ \ delta (t) = \ lim _ {\ epsilon \ to \ infty} x (t) $ est appelé signal d'impulsion unitaire. Ce signal tend vers l'infini lorsque t = 0 et tend vers zéro lorsque t ≠ 0 de sorte que l'aire sous sa courbe soit toujours égale à un. La fonction delta a une amplitude nulle partout où excunit_impulse.jpgept à t = 0.

Propriétés du signal d'impulsion d'unité

• δ (t) est un signal pair.
• δ (t) est un exemple de signal ni d'énergie ni de puissance (NENP).
• La zone du signal d'impulsion d'unité peut être écrite sous la forme;
$$ A = \ int _ {- \ infty} ^ {\ infty} \ delta (t) dt = \ int _ {- \ infty} ^ {\ infty} \ lim _ {\ epsilon \ to 0} x (t) dt = \ lim _ {\ epsilon \ to 0} \ int _ {- \ infty} ^ {\ infty} [x (t) dt] = 1 $$
• Le poids ou la force du signal peut s'écrire;
$$ y (t) = A \ delta (t) $$
• La zone du signal d'impulsion pondéré peut être écrite comme -
$$ y (t) = \ int _ {- \ infty} ^ {\ infty} y (t) dt = \ int _ {- \ infty} ^ {\ infty} A \ delta (t) = A [\ int _ {- \ infty} ^ {\ infty} \ delta (t) dt] = A = 1 = Wigthedimpulse $$

Signal d'étape de l'unité

Un signal qui satisfait les deux conditions suivantes -

• $ U (t) = 1 (quand \ quad t \ geq 0) et $
• $ U (t) = 0 (lorsque \ quad t <0) $

est connu comme un signal de pas unitaire.

Il a la propriété de montrer la discontinuité à t = 0. Au point de discontinuité, la valeur du signal est donnée par la moyenne de la valeur du signal. Ce signal a été pris juste avant et après le point de discontinuité (selon les phénomènes de Gibb).

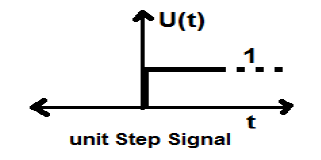
Si nous ajoutons un signal de pas à un autre signal de pas qui est mis à l'échelle du temps, le résultat sera l'unité. Il s'agit d'un signal de type puissance et la valeur de puissance est de 0,5. La valeur RMS (racine carrée moyenne) est de 0,707 et sa valeur moyenne est également de 0,5

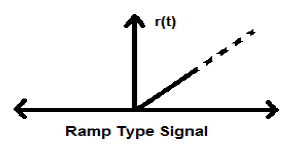
Signal de rampe

L'intégration du signal de pas donne un signal de rampe. Il est représenté par r (t). Le signal de rampe satisfait également la condition $ r (t) = \ int _ {- \ infty} ^ {t} U (t) dt = tU (t) $. Ce n'est ni un signal de type énergie ni puissance (NENP).

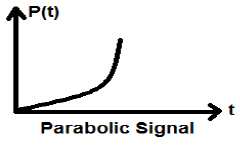
Signal parabolique

L'intégration du signal Ramp conduit au signal parabolique. Il est représenté par p (t). Le signal parabolique satisfait également la condition $ p (t) = \ int _ {- \ infty} ^ {t} r (t) dt = (t ^ {2} / 2) U (t) $. Ce n'est ni un signal de type énergie ni puissance (NENP).

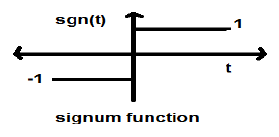
Fonction Signum

Cette fonction est représentée par

$$ sgn (t) = \ begin {cases} 1 & pour \ quad t> 0 \\ - 1 & pour \ quad t <0 \ end {cases} $$

C'est un signal de type puissance. Sa valeur de puissance et ses valeurs RMS (Root mean square) sont toutes deux égales à 1. La valeur moyenne de la fonction signum est zéro.

Fonction Sinc

C'est aussi une fonction du sinus et s'écrit -

$$ SinC (t) = \ frac {Sin \ Pi t} {\ Pi T} = Sa (\ Pi t) $$

Propriétés de la fonction Sinc

• C'est un signal de type énergétique.

• $ Sinc (0) = \ lim_ {t \ à 0} \ frac {\ sin \ Pi t} {\ Pi t} = 1 $

• $ Sinc (\ infty) = \ lim_ {t \ to \ infty} \ frac {\ sin \ Pi \ infty} {\ Pi \ infty} = 0 $ (La plage de sinπ∞ varie entre -1 et +1 mais tout est divisé par l'infini est égal à zéro)

• Si $ \ sin c (t) = 0 => \ sin \ Pi t = 0 $

  $ \ Flèche droite \ Pi t = n \ Pi $

  $ \ Flèche droite t = n (n \ neq 0) $

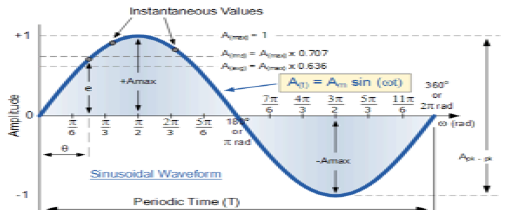
Signal sinusoïdal

Un signal, qui est de nature continue, est appelé signal continu. Le format général d'un signal sinusoïdal est

$$ x (t) = A \ sin (\ omega t + \ phi) $$

Ici,

A = amplitude du signal

ω = Fréquence angulaire du signal (mesurée en radians)

φ = Angle de phase du signal (mesuré en radians)

La tendance de ce signal est de se répéter après une certaine période de temps, c'est pourquoi on l'appelle signal périodique. La période de temps du signal est donnée comme;

$$ T = \ frac {2 \ pi} {\ omega} $$

La vue schématique du signal sinusoïdal est illustrée ci-dessous.

Fonction rectangulaire

Un signal est dit de type fonction rectangulaire s'il satisfait à la condition suivante -

$$ \ pi (\ frac {t} {\ tau}) = \ begin {cases} 1, & pour \ quad t \ leq \ frac {\ tau} {2} \\ 0, & Sinon \ end {cases} $$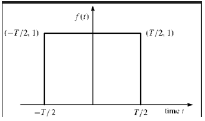

Étant symétrique par rapport à l'axe Y, ce signal est appelé signal pair.

Signal d'impulsion triangulaire

Tout signal satisfaisant à la condition suivante est appelé signal triangulaire.

$$ \ Delta (\ frac {t} {\ tau}) = \ begin {cases} 1 - (\ frac {2 | t |} {\ tau}) & pour | t | <\ frac {\ tau} { 2} \\ 0 & pour | t |> \ frac {\ tau} {2} \ end {cases} $$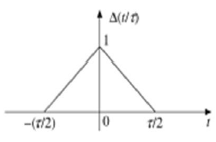

Ce signal est symétrique par rapport à l'axe Y. Par conséquent, il est également appelé signal pair.