Traitement numérique du signal - Définition des signaux
Définition
Tout ce qui porte des informations peut être appelé comme signal. Il peut également être défini comme une quantité physique qui varie avec le temps, la température, la pression ou avec toute variable indépendante telle que le signal vocal ou le signal vidéo.
Le processus de fonctionnement dans lequel les caractéristiques d'un signal (amplitude, forme, phase, fréquence, etc.) subissent un changement est appelé traitement du signal.
Note- Tout signal indésirable interférant avec le signal principal est appelé bruit. Ainsi, le bruit est aussi un signal mais indésirable.
Selon leur représentation et leur traitement, les signaux peuvent être classés en diverses catégories dont les détails sont décrits ci-dessous.
Signaux de temps continus
Les signaux à temps continu sont définis le long d'un continuum de temps et sont donc représentés par une variable indépendante continue. Les signaux à temps continu sont souvent appelés signaux analogiques.
Ce type de signal montre une continuité à la fois en amplitude et en temps. Celles-ci auront des valeurs à chaque instant. Les fonctions sinus et cosinus sont le meilleur exemple de signal à temps continu.
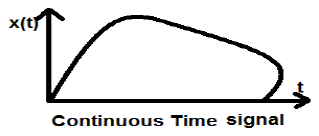
Le signal montré ci-dessus est un exemple de signal de temps continu car nous pouvons obtenir la valeur du signal à chaque instant.
Signaux temporels discrets
Les signaux, qui sont définis à des instants discrets, sont appelés signaux discrets. Par conséquent, chaque variable indépendante a une valeur distincte. Ainsi, ils sont représentés comme une séquence de nombres.
Bien que les signaux vocaux et vidéo aient le privilège d'être représentés dans un format à la fois continu et discret; dans certaines circonstances, ils sont identiques. Les amplitudes présentent également des caractéristiques discrètes. Un exemple parfait de ceci est un signal numérique; dont l'amplitude et le temps sont tous deux discrets.
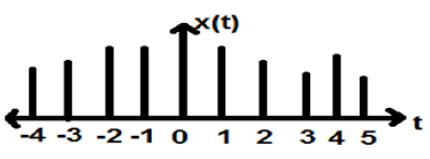
La figure ci-dessus représente la caractéristique d'amplitude discrète d'un signal discret sur une période de temps. Mathématiquement, ces types de signaux peuvent être formularisés comme;
$$ x = \ gauche \ {x \ gauche [n \ droite] \ droite \}, \ quad - \ infty <n <\ infty $$Où, n est un entier.
C'est une séquence de nombres x, où le n ième nombre de la séquence est représenté par x [n].