DSP - Opérations sur la différenciation des signaux
Deux opérations très importantes effectuées sur les signaux sont la différenciation et l'intégration.
Différenciation
La différenciation de tout signal x (t) signifie une représentation de la pente de ce signal par rapport au temps. Mathématiquement, il est représenté par;
$$ x (t) \ rightarrow \ frac {dx (t)} {dt} $$Dans le cas de la différenciation OPAMP, cette méthodologie est très utile. Nous pouvons facilement différencier un signal graphiquement plutôt que d'utiliser la formule. Cependant, la condition est que le signal doit être de type rectangulaire ou triangulaire, ce qui se produit dans la plupart des cas.
| Signal d'origine | Signal différencié |
|---|---|
| Rampe | Étape |
| Étape | Impulsion |
| Impulsion | 1 |
Le tableau ci-dessus illustre la condition du signal après avoir été différencié. Par exemple, un signal de rampe se convertit en un signal de pas après différenciation. De même, un signal de pas unitaire devient un signal d'impulsion.
Exemple
Soit le signal qui nous est donné $ x (t) = 4 [r (t) -r (t-2)] $. Lorsque ce signal est tracé, il ressemblera à celui du côté gauche de la figure ci-dessous. Maintenant, notre objectif est de différencier le signal donné.
Pour commencer, nous allons commencer à différencier l'équation donnée. On sait que le signal de rampe après différenciation donne un signal de pas unitaire.
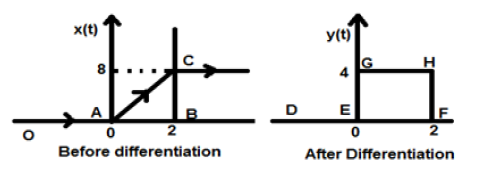
Ainsi, notre signal résultant y (t) peut s'écrire;
$ y (t) = \ frac {dx (t)} {dt} $
$ = \ frac {d4 [r (t) -r (t-2)]} {dt} $
$ = 4 [u (t) -u (t-2)] $
Maintenant, ce signal est tracé finalement, ce qui est montré dans le côté droit de la figure ci-dessus.