Statistiques - Distribution bêta

La distribution bêta représente une distribution de probabilité continue paramétrée par deux paramètres de forme positifs, $ \ alpha $ et $ \ beta $, qui apparaissent comme des exposants de la variable aléatoire x et contrôlent la forme de la distribution.

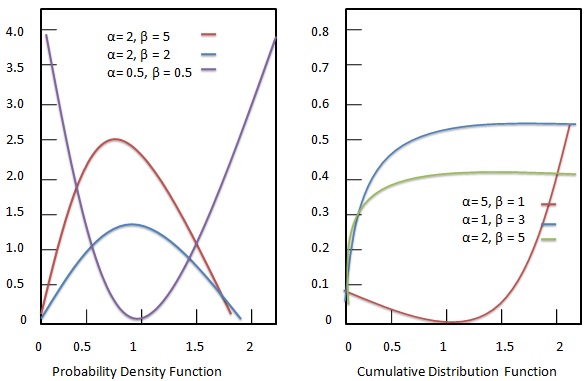
Fonction de densité de probabilité

La fonction de densité de probabilité de la distribution bêta est donnée comme suit:

Formule

$ {f (x) = \ frac {(xa) ^ {\ alpha-1} (bx) ^ {\ beta-1}} {B (\ alpha, \ beta) (ba) ^ {\ alpha + \ beta- 1}} \ hspace {.3in} a \ le x \ le b; \ alpha, \ beta> 0 \\ [7pt] \, où \ B (\ alpha, \ beta) = \ int_ {0} ^ {1} {t ^ {\ alpha-1} (1-t) ^ { \ beta-1} dt}} $

Où -

$ {\ alpha, \ beta} $ = paramètres de forme.
$ {a, b} $ = limites supérieure et inférieure.
$ {B (\ alpha, \ beta)} $ = Fonction bêta.

Distribution bêta standard

Dans le cas où les limites supérieure et inférieure sont 1 et 0, la distribution bêta est appelée distribution bêta standard. Il est conduit par la formule suivante:

Formule

$ {f (x) = \ frac {x ^ {\ alpha-1} (1-x) ^ {\ beta-1}} {B (\ alpha, \ beta)} \ hspace {.3in} \ le x \ le 1; \ alpha, \ beta> 0} $

Fonction de distribution cumulative

La fonction de distribution cumulative de la distribution bêta est donnée comme suit:

Formule

$ {F (x) = I_ {x} (\ alpha, \ beta) = \ frac {\ int_ {0} ^ {x} {t ^ {\ alpha-1} (1-t) ^ {\ beta- 1} dt}} {B (\ alpha, \ beta)} \ hspace {.2in} 0 \ le x \ le 1; p, \ beta> 0} $

Où -

$ {\ alpha, \ beta} $ = paramètres de forme.
$ {a, b} $ = limites supérieure et inférieure.
$ {B (\ alpha, \ beta)} $ = Fonction bêta.

Il est également appelé rapport de fonction bêta incomplet.