Statistiques - Modèles de données
Les modèles de données sont très utiles lorsqu'ils sont dessinés graphiquement. Modèles de données généralement décrits en termes de caractéristiques telles que le centre, l'étalement, la forme et d'autres propriétés inhabituelles. D'autres étiquettes descriptives spéciales sont symétriques, en forme de cloche, asymétriques, etc.
Centre
Le centre d'une distribution, graphiquement, est situé à la médiane de la distribution. Une telle charte graphique montre que près de la moitié des observations sont de chaque côté. La hauteur de chaque colonne indique la fréquence des observations.
Propagé
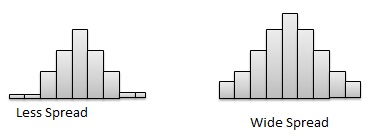
L'étalement d'une distribution fait référence à la variation des données. Si l'ensemble des observations couvre une large gamme, la propagation est plus grande. Si les observations sont centrées autour d'une seule valeur, alors l'écart est plus petit.
Forme
La forme d'une distribution peut être décrite en utilisant les caractéristiques suivantes.
Symmetry - En distribution symétrique, le graphe peut être divisé au centre de telle sorte que chaque moitié soit une image miroir de l'autre.

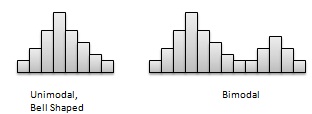
Number of peaks.- Distributions avec un ou plusieurs pics. La distribution avec un pic clair est appelée unimodale, et la distribution avec deux pics clairs est appelée bimodale. Une distribution symétrique de pic unique au centre, est appelée en forme de cloche.
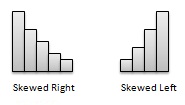
Skewness- Certaines distributions peuvent avoir plusieurs observations d'un côté du graphique que de l'autre. On dit que les distributions ayant moins d'observations vers des valeurs inférieures sont biaisées à droite; et les distributions avec moins d'observations vers des valeurs inférieures sont dites biaisées à gauche.
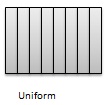
Uniform - Lorsque l'ensemble d'observations n'a pas de pic et que les données sont réparties de manière égale sur toute l'étendue de la distribution, la distribution est appelée distribution uniforme.
Caractéristiques inhabituelles
Les caractéristiques inhabituelles communes des modèles de données sont les lacunes et les valeurs aberrantes.
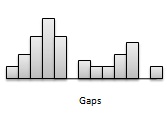
Gaps- Gaps pointe vers des zones d'une distribution n'ayant aucune observation. La figure suivante présente un écart car il n'y a aucune observation au milieu de la distribution.
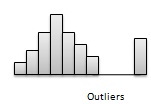
Outliers- Les distributions peuvent être caractérisées par des valeurs extrêmes qui diffèrent grandement de l'autre ensemble de données d'observation. Ces valeurs extrêmes sont appelées des valeurs aberrantes. La figure suivante illustre une distribution avec une valeur aberrante.