Statistiques - Diagramme de Venn

Le diagramme de Venn est un moyen de représenter visuellement la relation entre des groupes d'entités ou d'objets. Les diagrammes de Venn sont composés de cercles où chaque cercle représente un ensemble complet. Le diagramme de Venn peut avoir des cercles illimités mais généralement deux ou trois cercles sont préférés sinon le diagramme devient trop complexe.

Étapes pour dessiner un diagramme de Venn

Considérez les groupes de personnes suivants:

Cricket Players - $ C = \ {Ram, Shyam, Mohan, Rohan, Ramesh, Suresh \} $
Hockey Players - $ H = \ {Ramesh, Naresh, Mahesh, Leela, Sunita \} $

Étape 1: Dessinez un rectangle et étiquetez-le comme joueurs.

Étape 2: Dessinez deux cercles et étiquetez-les comme Cricket et Hockey. Assurez-vous que les cercles se chevauchent.

Étape 3: Écrivez les noms à l'intérieur du cercle si nécessaire. Les noms communs doivent appartenir à la région commune.

syndicat

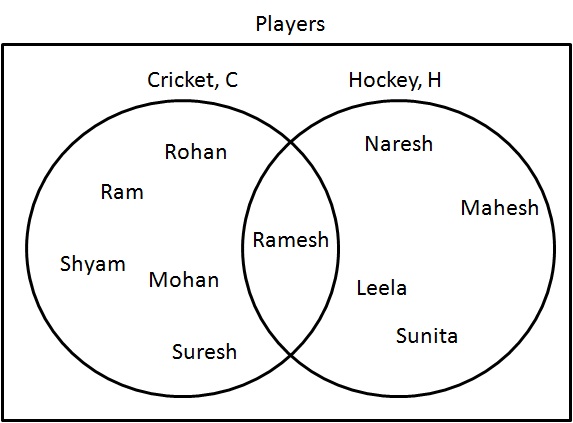
Union ($ \ cup $) représente un ensemble où les éléments sont présents dans toutes les catégories mais ne sont pas répétés.

Exemple

Problem Statement:

Dessinez un diagramme de Venn de $ C \ cup H $.

Solution:

Étape 1: Déterminez les joueurs qui jouent au cricket ou au hockey. Dessinez-les comme suit:

$ C \ cup H = \ {Ram, Shyam, Mohan, Rohan, Ramesh, Suresh, Naresh, Mahesh, Leela, Sunita \} $.

Intersection

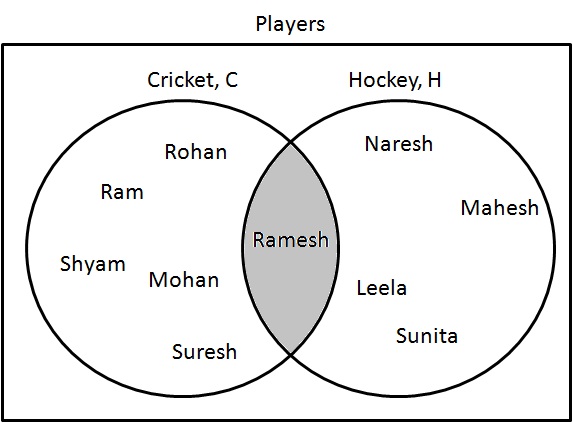
L'intersection ($ \ cap $) représente un ensemble où les éléments sont présents dans les deux catégories.

Exemple

Problem Statement:

Dessinez un diagramme de Venn de $ C \ cap H $.

Solution:

Étape 1: Déterminez les joueurs qui jouent au cricket et au hockey. Dessinez-les comme suit:

$ C \ cap H = \ {Ramesh \} $.

Différence

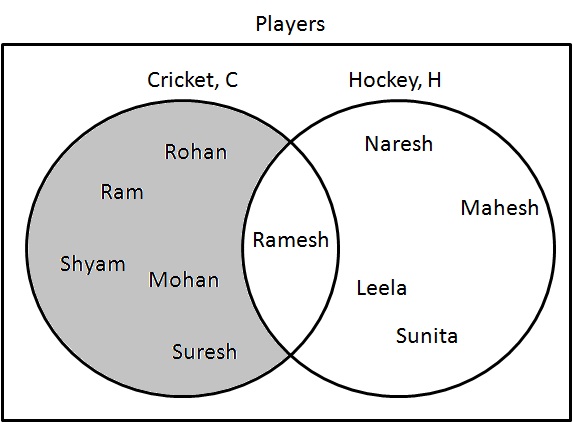
La différence ($ - $) représente un ensemble où les éléments ne sont présents que dans une catégorie et pas dans une autre.

Exemple

Problem Statement:

Dessinez un diagramme de Venn de $ C - H $.

Solution:

Étape 1: Déterminez les joueurs qui ne jouent qu'au cricket. Dessinez-les comme suit:

$ C - H = \ {Ram, Shyam, Mohan, Rohan, Suresh \} $.