Statistiques - Théorème de la limite centrale
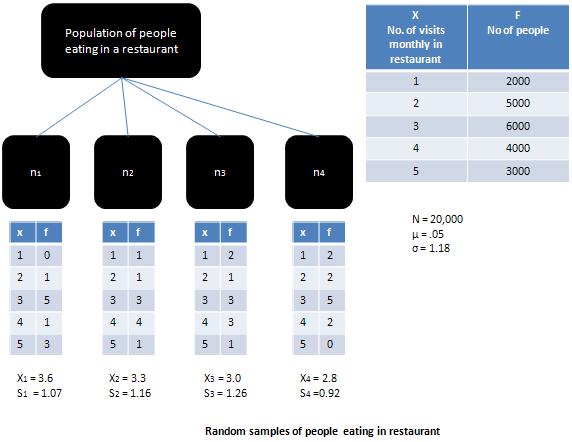
Si la population à partir de laquelle l'échantillon a été tiré est une population normale, sample means serait égal à la moyenne de la population et le sampling distributionserait normal. Lorsque plus la population est asymétrique, comme c'est le cas illustré dans la figure, alors lesampling distribution aurait tendance à se rapprocher de la distribution normale, à condition que l'échantillon soit grand (c'est-à-dire supérieur à 30).
Selon Central Limit Theorem, pour des échantillons suffisamment grands de taille supérieure à 30, la forme du sampling distribution deviendra de plus en plus comme un normal distribution, quelle que soit la forme de la population parentale. Ce théorème explique la relation entre lepopulation distribution et sampling distribution. Il met en évidence le fait que s'il existe un ensemble d'échantillons suffisamment grand,sampling distribution des approches moyennes normal distribution. L'importance du théorème central limite a été résumée par Richard. I. Levin dans les mots suivants:
L'importance du théorème central de la limite réside dans le fait qu'il nous permet d'utiliser des statistiques d'échantillonnage pour faire des inférences sur les paramètres de la population sans rien savoir sur la forme de la distribution de fréquence de cette population autre que ce que nous pouvons obtenir de l'échantillon.