Statistiques - Distribution normale
Une distribution normale est un agencement d'un ensemble de données dans lequel la plupart des valeurs se regroupent au milieu de la plage et le reste diminue symétriquement vers l'un ou l'autre extrême. La taille est un exemple simple de quelque chose qui suit un modèle de distribution normal: la plupart des gens sont de taille moyenne, le nombre de personnes plus grandes et plus courtes que la moyenne est assez égal et un très petit nombre (et encore à peu près équivalent) de personnes sont soit extrêmement haut ou extrêmement court, voici un exemple de courbe de distribution normale:
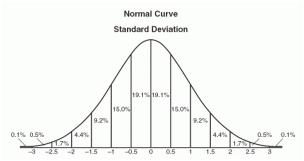
Une représentation graphique d'une distribution normale est parfois appelée courbe en cloche en raison de sa forme évasée. La forme précise peut varier en fonction de la répartition de la population mais le pic est toujours au milieu et la courbe est toujours symétrique. Dans une distribution normale, le mode moyen et la médiane sont tous les mêmes.
Formule
$ {y = \ frac {1} {\ sqrt {2 \ pi}} e ^ {\ frac {- (x - \ mu) ^ 2} {2 \ sigma}}} $
Où -
$ {\ mu} $ = Moyenne
$ {\ sigma} $ = écart type
$ {\ pi \ approx 3.14159} $
$ {e \ approx 2.71828} $
Exemple
Problem Statement:
Une enquête sur le temps de trajet quotidien a donné ces résultats (en minutes):
| 26 | 33 | 65 | 28 | 34 | 55 | 25 | 44 | 50 | 36 | 26 | 37 | 43 | 62 | 35 | 38 | 45 | 32 | 28 | 34 |
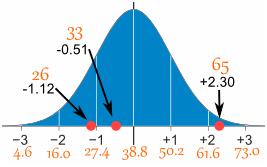
La moyenne est de 38,8 minutes et l'écart type est de 11,4 minutes. Convertissez les valeurs en scores z et préparez le graphique de distribution normale.
Solution:
La formule du z-score que nous utilisons:
$ {z = \ frac {x - \ mu} {\ sigma}} $
Où -
$ {z} $ = le "score z" (score standard)
$ {x} $ = la valeur à normaliser
$ {\ mu} $ = moyenne
$ {\ sigma} $ = l'écart type
Pour convertir 26:
Soustrayez d'abord la moyenne: 26-38,8 = -12,8,
Puis divisez par l'écart type: -12,8 / 11,4 = -1,12
Donc, 26 est -1,12 écart type par rapport à la moyenne
Voici les trois premières conversions.
| Valeur d'origine | Calcul | Score standard (score z) |
|---|---|---|
| 26 | (26-38,8) / 11,4 = | -1,12 |
| 33 | (33-38,8) / 11,4 = | -0,51 |
| 65 | (65-38,8) / 11,4 = | -2,30 |
| ... | ... | ... |
Et ici, ils représentent graphiquement: