Statistiques - Analyse résiduelle
L'analyse des résidus est utilisée pour évaluer la pertinence d'un modèle de régression linéaire en définissant les résidus et en examinant les graphiques des tracés des résidus.
Résiduel
Résiduel ($ e $) fait référence à la différence entre la valeur observée ($ y $) et la valeur prédite ($ \ hat y $). Chaque point de données a un résidu.
$ {valeur résiduelle = valeur observée - valeur prédite \\ [7pt] e = y - \ hat y} $
Tracé résiduel
Un graphique résiduel est un graphique dans lequel les résidus sont sur l'axe vertical et la variable indépendante est sur l'axe horizontal. Si les points sont dispersés au hasard autour de l'axe horizontal, un modèle de régression linéaire est approprié pour les données; sinon, choisissez un modèle non linéaire.
Types de tracé résiduel
L'exemple suivant montre quelques modèles dans les tracés résiduels.
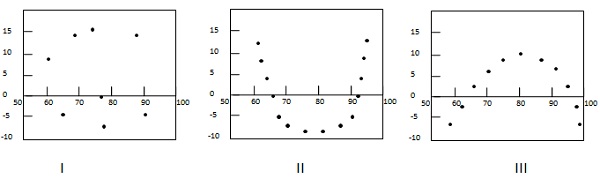
Dans le premier cas, les points sont dispersés au hasard. Le modèle de régression linéaire est donc préféré. Dans le deuxième et le troisième cas, les points sont dispersés de manière non aléatoire et suggèrent qu'une méthode de régression non linéaire est préférée.
Exemple
Problem Statement:
Vérifiez où un modèle de régression linéaire est approprié pour les données suivantes.
| $ x $ | 60 | 70 | 80 | 85 | 95 |
|---|---|---|---|---|---|
| $ y $ (valeur réelle) | 70 | 65 | 70 | 95 | 85 |
| $ \ hat y $ (valeur prédite) | 65.411 | 71.849 | 78,288 | 81,507 | 87,945 |
Solution:
Step 1: Calculez les résidus pour chaque point de données.
| $ x $ | 60 | 70 | 80 | 85 | 95 |
|---|---|---|---|---|---|
| $ y $ (valeur réelle) | 70 | 65 | 70 | 95 | 85 |
| $ \ hat y $ (valeur prédite) | 65.411 | 71.849 | 78,288 | 81,507 | 87,945 |
| $ e $ (résiduel) | 4,589 | -6.849 | -8,288 | 13,493 | -2,945 |
Step 2: - Dessinez le graphe résiduel.
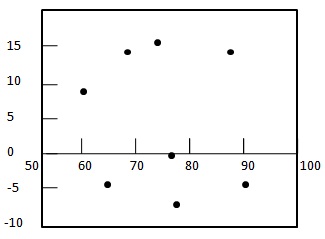
Step 3: - Vérifiez le caractère aléatoire des résidus.
Ici, le tracé des résidus présente un modèle aléatoire - Le premier résidu est positif, les deux suivants sont négatifs, le quatrième est positif et le dernier résiduel est négatif. Le motif étant assez aléatoire, ce qui indique qu'un modèle de régression linéaire est approprié pour les données ci-dessus.